什么是矩阵
什么是矩阵
在线性代数中,有这样一个定义:
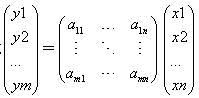
由数域P中m×n个数aij(i=1,2,…m;j=1,2,…,n)排列成一个m行n列的矩形数表
 称为一个数域P上的m×n矩阵,其中数aij称为矩阵的(i,j)元素。
称为一个数域P上的m×n矩阵,其中数aij称为矩阵的(i,j)元素。
这个定义,只说到了矩阵的外在形式,而没有谈矩阵的内涵,矩阵是线性空间V1到线性空间V2的一个线性映射的表示。线性空间在前面已经介绍过了,下面定义线性映射、线性映射的矩阵表示。
定义线性映射:
Æ(ɑ+ß) = Æ(ɑ) + Æ(ß)
Æ(kɑ) = kÆ(ɑ)
£(V1,V2)表示从线性空间V1到线性空间V2的所有线性映射组成的集合,由线性映射的加法和数乘的定义可知,£(V1,V2)本身就构成数域P上的线性空间,(设线性映射Æ、Б,根据线性映射的加法和数乘定义,验证Æ、Б的加法运算的四条规则以及k、Æ的数乘运算的四条规则,符合线性空间的定义)空间中的向量就是线性映射Æ。
线性映射的矩阵表示:
矩阵,是由线性映射导出的,是线性映射的一种表达形式,这才是矩阵的本质。
设V1是数域P上的n维线性空间,ξ1,ξ2,…ξn是V1的一组基,V2是数域P上的m维线性空间,η1,η2,…,ηm是V2的一组基,Æ是V1到V2的一个线性映射。
则
Æ(ξ1,ξ2,…ξn) = (Æ(ξ1), Æ(ξ2),… Æ(ξn)) = (η1,η2,…,ηm)A
其中
矩阵A称为线性映射Æ在V1的基ξ1,ξ2,…ξn和V2的基η1,η2,…,ηm下的矩阵,矩阵A完全由线性映射本身以及V1的基ξ1,ξ2,…ξn和V2的基η1,η2,…,ηm唯一确定。基一旦给定,一个线性映射对应一个矩阵;如果线性映射确定,给定V1或V2基不一样,则线性映射所对应的矩阵是不同的,但它们之间的关系是相抵的。
可见,矩阵是线性映射的表示,£(V1,V2)所构成的线性空间同构于矩阵空间Pm×n,这个矩阵空间的维数为线性空间V2的维数乘以线性空间V1的维数,即m×n。矩阵是线性映射的表示,也是矩阵空间Pm×n中的向量。(嘿嘿J,听起来很拗口!)
既然映射空间£(V1,V2)同构于矩阵空间Pm×n,对线性映射的研究转化为对矩阵的研究,线性映射的加法转化为矩阵的加法,线性映射的数乘转化为矩阵的数乘,特别地,映射的乘积ƒ2·ƒ1转化矩阵的乘积。对矩阵的秩、方阵的特征值与特征向量等性质的研究,就是在研究线性映射的性质和规律。
把线性空间V1中的向量ɑ映射到线性空间V2中向量ß,给定V1,V2一组基,则线性映射所对应矩阵A是确定的,即ß = Aɑ或
矩阵A的秩,反映了V1-> V2线性映射值域空间R(Æ)的维数dim(R(Æ)),而dim(V1)-dim(R(Æ))=dim(Ker(Æ)),可这么理解,损失掉的空间维数,其实是被映射到V2的零空间。
特殊地,dim(V1)=dim(V2),(线性空间维数相同即同构),则V1-> V2线性映射称为线性变换。线性变换所对应的矩阵是一个方阵,同一线性变换在不同基对下的矩阵是相似的,选取线性空间中的一组基使得线性变换在这组基下的矩阵具有简单的形式,所以,就需要研究矩阵的特征值与特征向量的问题,研究矩阵可对角化或相似标准型。
有一类特殊的线性变换,在同一个内积空间中,线性变换保持内积不变,称为酉(正交)变换。酉(正交)变换所对应的矩阵,称为酉(正交)阵,即
ATA = AAT = I 或 AHA = AAH = I
定义 设Æ是n维酉(欧式)空间V上的线性变换,如果对任意向量ɑ、ß∈V都有
(Æ(ɑ), Æ(ß))= (ɑ, ß)
则称Æ是V的酉(正交)变换。
数字图象处理的时域到频域的转换中所采用的傅立叶变换,DCT变换等都属于酉(正交)变换,不改变能量即向量的内积,只是换了一组基,类似于解析几何的旋转变换,变换后的系数,就是向量在这组基下的新的坐标。
£(V1,V2)表示所有从n维线性空间V1到m维线性空间V2的线性映射的集合,按线性映射的加法和数乘的定义构成线性空间,维数是m×n,同构于一个Pm×n的矩阵线性空间,矩阵线性空间中的向量是矩阵。一个m×n的矩阵是n维线性空间V1到m维线性空间V2的一个线性映射的表示。同一线性映射在不同基对下所对应的矩阵是相抵的(或者叫等价的),秩相同,即线性映射在V2中形成的值域空间R(Æ)的维数;V-> V线性映射即线性变换,同一线性变换在不同基下所对应的矩阵是相似的,相似关系也是一种相抵关系,具有相同的秩,即线性变换的值域空间R(Æ)的维数。可见,秩是线性映射的不变量,是一类线性映射的本质特征。既然一个数字矩阵是一个线性映射的表示,那么矩阵值函数就是一类线性映射的表示,从矩阵向量空间的角度来看,一个数字矩阵在空间中是一个点,一个矩阵值函数在空间是一个超面,(至少有一个分量是一个变量)。