目录
- 模拟赛简要题解与心得
- T1 方格纸与直线
- 题解
- T2 探险
- 题解
- 3.苹果树
- 题解
- 心得
模拟赛简要题解与心得
最近我的心态炸了,写此博客纪念调侃一下.
T1 方格纸与直线
【题目描述】
小林有一张 n 行 m 列的方格纸,如下所示。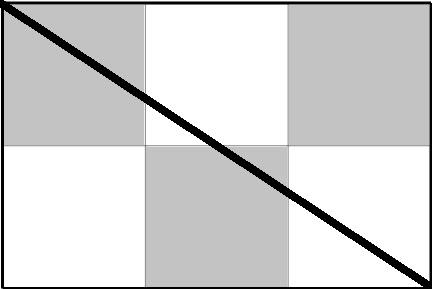
该方格纸黑白相间,且第一行第一列为黑色。顽皮的亮亮在方格纸上画了一
条连接左上角和右下角的线段。小林看到方格纸后,马上算出了位于黑色区域的
线段的长度之和占整条线段长度的比值。现在,他想考考你会不会算。
【输入格式】
一行两个整数 n 和 m。
【输出格式】
输出一个分数,即题目中所求的比值,用两个由’/’分隔的互质整数表示。
【样例输入】
4 6
【样例输出】
1/2
【数据规模】
对于 50%的数据,n, m <= 10^6;
对于 100%的数据,1 <= n,m <= 10^9。
题解
找规律的好题,但是还是因为时间问题错失了满分的机会.
题目要求的是比值,故当 m 与 n 不互质时,我们可以求出 m 和 n 的最大
公约数 d,并将 m /= d, n /= d,并不影响结果。故我们现在假定 m 和 n 互质。若m 和 n 中有一个为偶数, 那么根据对称性, 答案就是 1/2。 如果 m 和 n 均为奇数,
那么答案就是\((n*m+1) / (2*m*n)\)。
T2 探险
【题目描述】
小林和亮亮来到森林中探险, 森林中有一条长度为 S 的小路 (编号从 1 到 S) ,
且在小路上时常会起雾,亮亮也可以用神光让雾消散。
小林则关心在某一位置的视野。若位置 x 有浓雾,则位置 x 的视野为 0。若
从 x 一直到 S 或从 x 一直到 1 全都没有浓雾,则视野为INF。其他情况下,位置x的视野为\(max{R - L + 1}\)
要满足这个区间内没有浓雾的产生.
具体来说,会有以下事件发生:
1、“1 L R”小路的[L, R]部分产生了浓雾;
2、“2 L R”小路的[L, R]部分浓雾散去了。
3、“3 X” 查询 X 点的视野。
一开始,小路上没有任何浓雾。
【输入格式】
第一行一个整数,为小路的长度 S。
第二行一个整数,为事件数 Q。
接下来 Q 行,每行一个事件,格式如题目描述。
【输出格式】
对于每一个询问事件,输出一个整数或一行字符串“INF”,代表所求视野。
【样例输入】
5
5
1 2 4
3 1
3 4
2 3 3
3 3
【样例输出】
INF
0
1
【数据规模】
对于 40%的数据,SQ <= 510^7。
对于 100%的数据,2≤S≤100,000,2≤Q≤200,000,1≤L≤R≤S,1≤X≤S。
题解
T1推了很长时间,忘记找规律了,结果T2考场一眼出正解却不敢写.写了分块.不知道怎么的就过了.虽然过了,花了我1.5h的时间,so sad.
正解:线段树,维护区间的和.如果这个点是雾,则这个点的值为1.然后二分最远到达的l,r即可.
放上分块的代码吧:
CODE:
#include
#include
#include
#include
using namespace std;
const int maxN = 100000 + 7;
int a[maxN],belong[maxN],R[maxN],L[maxN];
int sum[maxN];
int vis[maxN];
int n;
inline int read() {
int x = 0,f = 1;char c = getchar();
while(c < '0' || c > '9') {if(c == '-')f = -1;c = getchar();}
while(c >= '0' && c <= '9') {x = x * 10 + c - '0';c = getchar();}
return x * f;
}
void pushdown(int now) {
if(vis[now] == 1) {
for(int i = L[now];i <= R[now];++ i) a[i] = 1;
sum[now] = R[now] - L[now] + 1;
}
if(vis[now] == 2) {
for(int i = L[now];i <= R[now];++ i) a[i] = 0;
sum[now] = 0;
}
vis[now] = 0;
return ;
}
inline void change_done(int l,int r) {
int belong_l = belong[l],belong_r = belong[r];
if(belong_l == belong_r) {
if(vis[belong_l]) pushdown(belong_l);
for(int i = l;i <= r;++ i) a[i] = 1;
sum[belong_l] = 0;
for(int i = L[belong_l];i <= R[belong_l];++ i)
if(a[i]) sum[belong_l] ++;
return;
}
for(int i = belong_l + 1;i < belong_r;++ i) vis[i] = 1,sum[i] = R[i] - L[i] + 1;
if(vis[belong_l]) pushdown(belong_l);
if(vis[belong_r]) pushdown(belong_r);
for(int i = l;i <= R[belong_l];++ i) a[i] = 1;
for(int i = L[belong_r];i <= r;++ i) a[i] = 1;
sum[belong_l] = sum[belong_r] = 0;
for(int i = L[belong_l];i <= R[belong_l];++ i)
if(a[i]) sum[belong_l] ++;
for(int i = L[belong_r];i <= R[belong_r];++ i)
if(a[i]) sum[belong_r] ++;
return ;
}
inline void change_clear(int l,int r) {
int belong_l = belong[l],belong_r = belong[r];
if(belong_l == belong_r) {
if(vis[belong_l]) pushdown(belong_l);
for(int i = l;i <= r;++ i) a[i] = 0;
sum[belong_l] = 0;
for(int i = L[belong_l];i <= R[belong_l];++ i)
if(a[i]) sum[belong_l] ++;
return;
}
for(int i = belong_l + 1;i < belong_r;++ i) vis[i] = 2,sum[i] = 0;
if(vis[belong_l]) pushdown(belong_l);
if(vis[belong_r]) pushdown(belong_r);
for(int i = l;i <= R[belong_l];++ i) a[i] = 0;
for(int i = L[belong_r];i <= r;++ i) a[i] = 0;
sum[belong_l] = sum[belong_r] = 0;
for(int i = L[belong_l];i <= R[belong_l];++ i)
if(a[i]) sum[belong_l] ++;
for(int i = L[belong_r];i <= R[belong_r];++ i)
if(a[i]) sum[belong_r] ++;
return ;
}
inline int query(int pos) {
int Le = pos,Ri = pos;
int belong_pos = belong[pos];
if(vis[belong_pos]) pushdown(belong_pos);
if(a[pos]) {return 0;}
if(pos == n || pos == 1) return -1;
for(int i = pos;i <= R[belong_pos];++ i) {
if(!a[i]) Ri = i;
else break;
}
for(int i = pos - 1;i >= L[belong_pos];-- i) {
if(!a[i]) Le = i;
else break;
}
int belong_end = belong[n],belong_begin = belong[1];
if(vis[belong[Ri + 1]]) pushdown(belong[Ri + 1]);
if(!a[Ri + 1]) {
for(int j = belong_pos + 1;j <= belong_end;++ j) {
if(sum[j] != 0) break;
Ri = R[j];
}
if(vis[belong[Ri + 1]]) pushdown(belong[Ri + 1]);
for(int j = Ri + 1;j <= n;++ j) {
if(!a[j]) Ri = j;
else break;
}
}
if(vis[belong[Le - 1]]) pushdown(belong[Le - 1]);
if(!a[Le - 1]) {
for(int j = belong_pos - 1;j >= belong_begin;-- j) {
if(sum[j] != 0) break;
Le = L[j];
}
if(vis[belong[Le - 1]]) pushdown(belong[Le - 1]);
for(int j = Le - 1;j >= 1;-- j) {
if(!a[j]) Le = j;
else break;
}
}
if(Ri == n || Le == 1) return -1;
return Ri - Le + 1;
}
int main() {
freopen("explore.in","r",stdin);
freopen("explore.out","w",stdout);
n = read();
int m = read(),type,l,r,x;
int q = sqrt(n);
for(int i = 1;i <= n;++ i) belong[i] = i / q + 1;
for(int i = 1;i <= n;++ i) R[belong[i]] = i;
for(int i = n;i >= 1;-- i) L[belong[i]] = i;
while(m --) {
type = read();
if(type == 1) {
l = read();r = read();
change_done(l,r);
}
if(type == 2) {
l = read();r = read();
change_clear(l,r);
}
if(type == 3) {
x = read();
int tmp = query(x);
if(tmp == -1) {puts("INF");continue;}
printf("%d\n", tmp);
}
}
fclose(stdin);
fclose(stdout);
return 0;
} 线段树代码(STD):
#include
#include
#include
#include
#define fortodo(i, f, t) for (i = f; i <= t; i++)
using namespace std;
int lsd[200001], rsd[200001], lsid[200001], rsid[200001], cov[200001], segsize;
bool emp[200001];
int SEG_Build(int L, int R)
{
int Nid = ++segsize;
lsd[Nid] = L; rsd[Nid] = R;
emp[Nid] = true; cov[Nid] = 0;
if (L == R)
lsid[Nid] = rsid[Nid] = -1;
else
{
lsid[Nid] = SEG_Build(L, (L + R) / 2);
rsid[Nid] = SEG_Build((L + R) / 2 + 1, R);
};
return Nid;
};
bool SEG_Empty(int Nid)
{
if (cov[Nid] == 0) return true;
if (cov[Nid] == 1) return false;
return emp[Nid];
};
void SEG_Reemp(int Nid)
{
emp[Nid] = SEG_Empty(lsid[Nid]) && SEG_Empty(rsid[Nid]);
};
void SEG_Inherit(int Nid)
{
if (cov[Nid] == -1) return;
if (lsd[Nid] == rsd[Nid]) return;
cov[lsid[Nid]] = cov[Nid];
cov[rsid[Nid]] = cov[Nid];
cov[Nid] = -1;
SEG_Reemp(Nid);
};
void SEG_Paint(int Nid, int L, int R, int Color)
{
SEG_Inherit(Nid);
if ((L == lsd[Nid]) && (R == rsd[Nid]))
{
cov[Nid] = Color;
return;
};
int Div = (lsd[Nid] + rsd[Nid]) / 2;
if (L > Div) SEG_Paint(rsid[Nid], L, R, Color);
if (R <= Div) SEG_Paint(lsid[Nid], L, R, Color);
if ((L <= Div) && (R > Div))
{
SEG_Paint(lsid[Nid], L, Div, Color);
SEG_Paint(rsid[Nid], Div + 1, R, Color);
};
SEG_Reemp(Nid);
};
bool SEG_Query(int Nid, int L, int R)
{
SEG_Inherit(Nid);
if (SEG_Empty(Nid)) return true;
if ((L == lsd[Nid]) && (R == rsd[Nid])) return SEG_Empty(Nid);
int Div = (lsd[Nid] + rsd[Nid]) / 2;
if (L > Div) return SEG_Query(rsid[Nid], L, R);
if (R <= Div) return SEG_Query(lsid[Nid], L, R);
return SEG_Query(lsid[Nid], L, Div) && SEG_Query(rsid[Nid], Div + 1, R);
};
int S, Q;
int i, j;
int Opt, X, Y;
void Answer(int P)
{
if (!SEG_Query(1, P, P))
{
printf("0\n");
return;
};
if ((SEG_Query(1, 1, P)) || (SEG_Query(1, P, S)))
{
printf("INF\n");
return;
};
int L, R, M, Ans[2];
L = 2; R = P;
while (L < R)
{
M = (L + R) / 2;
if (SEG_Query(1, M, P))
R = M;
else
L = M + 1;
};
Ans[0] = L;
L = P; R = S - 1;
while (L < R)
{
M = (L + R + 1) / 2;
if (SEG_Query(1, P, M))
L = M;
else
R = M - 1;
};
Ans[1] = L;
printf("%d\n", Ans[1] - Ans[0] + 1);
};
int main()
{
freopen("explore.in", "r", stdin);
freopen("explore.out", "w", stdout);
scanf("%d%d", &S, &Q);
segsize = 0;
SEG_Build(1, S);
fortodo(i, 1, Q)
{
scanf("%d%d", &Opt, &X);
if (Opt != 3) scanf("%d", &Y);
if (Opt == 1) SEG_Paint(1, X, Y, 1);
if (Opt == 2) SEG_Paint(1, X, Y, 0);
if (Opt == 3) Answer(X);
};
return 0;
}; 3.苹果树
【题目描述】
小林有一棵苹果树,树上一共有 n 个节点,n-1 条边,每条边都有长度,且
有些节点上结有苹果。
亮亮希望砍掉苹果树的某些边,使得没有任意两个苹果在同一联通块中,并
且所砍去的边的长度之和最小。
【输入格式】
第一行两个整数 n, k, 分别表示树的结点数和含有苹果的结点数。 结点用 0 ~
n-1 标号。
接下来 n-1 行,每行三个数 x, y, z,表示一条从 x 到 y 权值为 z 的边。
接下来 k 行,每行一个数 x,表示编号为 x 的结点上结有一个苹果。
【输出格式】
只有一个整数,表示最小的长度之和。
【样例输入】
5 3
2 1 7
1 0 4
2 4 9
1 3 4
0
1
2
【样例输出】
11
【数据规模】
对于 40%的数据,n <= 20;
其中 10%的数据和另外 20%的数据,树的形态为一条链;
对于 100%的数据,2 <= n <= 100000,2 <= k <= n, 1 <= 边权 <= 1000000。
题解
实在是没有时间写暴力了,不然40的数据\(2^n\)枚举子集.再\(n\)判断联通块.
\(60\)的数据直接线段树即可.
剩下的应该是一个树形D.P
实在是没有时间了.
树形 DP。首先任取一个有苹果的结点为根,构建整棵树,接下来自底向上进行动态
规划。设 f[u]表示以 u 为根的子树中苹果互不连通,且子树中的苹果不与树外的苹果连通的
最小代价。g[u]表示以 u 为根的子树中苹果互不连通所需的最小代价。
那么当 u 上有苹果时,
g[u] = sum (f[v]) (v 为 u 的所有子节点) ;
f[u] = g[u] + pre[u] (pre[u]为 u 与其父节点连边的权值) 。
当 u 上无苹果时,
设 s[u] = sum (f[v]) (v 为 u 的所有子节点)
则 g[u] = min (s[u] - f[v] + g[v])
f[u] = min(s[u], g[u] + pre[u)]
心得
考场策略出现问题,T1没有找规律,T2一眼题没有写正解,T3没有时间看.
开场肝T1.
直接sb了.
以后模拟赛时应该通读一遍题目.
希望以后不犯类似的错误.