强化学习(三):动态规划求解MDP(Planning by Dynamic Programming)
上一节主要是引入了MDP(Markov decision process)的各种相关的定义与概念。最后得到了最优状态值函数 v∗(s) 和最优状态动作值函数 q∗(s,a) 的定义与公式。这一节主要是在已知模型的情况下利用动态规划来进行强化学习求解 v∗(s) 和 q∗(s,a) 。什么叫已知模型的情况?就是说上一节讲到的 <S,A,P,R,γ> ,这些都是已知的。求解的方法主要有两个,一个是策略迭代,另一个是值迭代。
本文基本参照了这篇文章的内容,再加上一点自己的理解,希望能够帮助到大家。
Dynamic Programming(动态规划)
首先什么是动态规划呢?相信大家对动态规划有一定的了解,就是一个问题的求解可以通过求解子问题而得到解决,就像递归一样。详细的动态规划理解大家可以在这里查看。
而MDP 刚好符合动态规划的性质,其中bellman方程就是递归结构。值函数存储了子问题的解决,这样在解决更进一步的子问题时就不用重头计算,而是可以直接取上一次的值函数来使用。
Iteration Policy Evaluation(迭代法策略评估)
- 问题:评估一个给定的策略 π 。
- 解决方法:利用bellman方程反向迭代。
具体做法:每次迭代过程中,用所有的状态s的第k次迭代得到的的 vk(s′) 来计算第k+1次的 vk+1(s) 的值。经过这种方法的反复迭代,最终是可以收敛到最优的 v∗(s) 。迭代的公式如下:
vk+1(s)=∑a∈Aπ(a|s)(Ras+γ∑s′∈SPass′vk(s′))例子:

* 即时奖励:上图是一个九宫格,左上角和右下角是终点,它们的reward是0,其他的状态,reward都是-1。
* 状态空间:除了灰色两个格子,其他都是非终点状态
* 动作空间:在每个状态下,都有四种动作可以执行,分别是上下左右(东西南北)。
* 转移概率:任何想要离开格子的动作将保持其状态不变,也就是原地不动。其他时候都是直接移动到下一个状态。所以状态转移概率是确定性的。
* 折扣因子: γ=1
* 当前策略:在任何状态下,agent都采取随机策略,也就是它的动作是随机选择的,即:
*
- 问题:评估在这个九宫格里给定的策略。也就是说,在策略给定的情况下(这里是随机策略),求解在该策略下所有状态的 v(s) 值。

上图中,每个格子的数字是对应状态的V值。图中只显示了迭代三次的结果,还需要一直迭代下去。大概在153次迭代之后,V值就收敛了。
注意,在我们迭代的过程中,我们并没有对策略进行修改,一直都是保持随机策略。而我们的目标是要得到最优策略,所以在迭代到V值收敛后,我们可以对策略进行改进(Policy Improvement)。我们可以使用贪婪算法来进行策略改进,即:
-
π∗=argmaxa∈A qπ(s,a)
- 由于值函数已经收敛了,所以此时用贪婪算法进行策略改进得到的策略就是最优策略了。
个人总结:上面讲的方法的前提是策略 π 在一开始就没有改变,只是通过不断地迭代计算 v(s) 的值,直到最后 v(s) 收敛才停止迭代。事实上,这样需要迭代很多次才会收敛,可能我们会想,我们可不可以每迭代计算一次 v(s) 的值,就改进一下我们的策略,而不是得到 v(s) 收敛了才来改进策略呢?所以接下来我们就来讲策略迭代,它就是这么干的。
Policy Iteration(策略迭代)
前面讲的九宫格的例子就是为了给策略迭代做铺垫。
策略迭代分为两部分,第一个部分是策略评估,第二部分是策略改进。所谓策略评估就是在当前的策略下计算 v(s) 的值。策略改进则是利用策略评估得到的 v(s) 来进行策略改进。然后继续重复策略评估,策略改进,直到最后收敛到最优策略。算法的伪代码如下:

上图中,代码第4行就是利用当前策略 π 对V值进行更新迭代。第11行就是利用更新后的V值来计算Q值,然后利用贪婪算法对策略进行更新。这里和上面的不同就在于,策略的评估与策略的改进是反复交替的,即从一个初始的策略(通常是随机策略)出发,先进行策略评估,然后改机策略,评估改进的策略,再进一步改进策略,……不断迭代直到策略收敛。
个人总结:值迭代是一开始不改变策略,一直迭代计算 v(s) 的值,直到最后 v(s) 收敛了。这时候再根据贪婪算法改进策略。而策略迭代则是每计算一次 v(s) 的值,就改进一次策略,然后利用改进的策略继续计算 v(s) 的值,这样去迭代。
Value Iteration
优化原则
任意一个最优策略可以被分为两部分:从状态s到到下一个状态s’采取了最优动作 A∗ ;在状态s’时遵循一个最优策略。所以如果我们求解出了 v∗(s′) 我们就可以利用下面的公式求解出 v∗(s) 。
值迭代的思想就是利用上面的公式进行迭代更新。下面是值迭代的总体方案:

注意图中 r(s,a) 与 Ras 是一样的,都是说在状态s下,采取动作a能够获得的即时奖励。
比如下面这个九宫格:
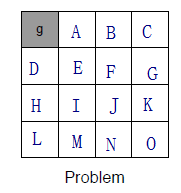
除了g点的reward=0,其他的状态reward=-1。终点是左上角写着g的灰色格,所以,在迭代的过程中,距离g最近的那两个格子(即A和D)的V(s)最先可以算出最大值。对于A来说,只要选择向左,就可以达到终点获得reward。而向右则没有奖赏。所以根据公式中的max,A就会选择左走,它的V值最大,所以第一次迭代它就已经可以获得最大值了,然后接下来就是对于B来说,第一次迭代向左和向右都一样,但是在第二次迭代中就会发现两次向左就可以达到最大值。
这就是值迭代的过程。除了g点的reward=0,其他的状态reward=-1。首先初始化每个状态(即从A到O)的V都为0。接着进行第一次迭代(即k=1),所以根据公式,k=1时的迭代为:
显然,由于 ∀s∈S:V1(s)=0 (即上图中的 V1 ),所以max都是一样的,所以就会导致 ∀s∈S:V2(s)=−1 (即上图中的 V2 )。
接着进行k=2时的迭代:
此时对于A状态来说,它会发现向右走和向下走得到的V是-2,而向左走的V是-1。因此max就起到作用了,从而让A点选择向左走,所以 V3(A)=−1 。而对于B点来说,它向左向右向下,它的周围都是-1.也就是采取任何动作,它得到的都是-2.所以 V3(A)=−2 。以此类推,直到每个状态的累积奖赏都不变。
动态规划的一些扩展
Asynchronous Dynamic Programming(异步动态规划)
我们前面所讲的都是基于同步迭代更新的。也就是第k+1次的结果都是利用第k次的结果来计算的,异步则表示第k次的迭代直接用第k次中先迭代好的值来计算。用公式表示则为:


第一个公式表示的是同步迭代更新,第二个公式表示异步迭代更新。
在异步更新的时候就有一个先后问题,就是哪个状态先更新,哪个状态后更新呢?这就是状态优先更新(Priortised Sweeping):对那些重要的状态优先更新。
参考:
David Silver强化学习公开课
https://zhuanlan.zhihu.com/p/28084955
《机器学习》周志华 清华大学出版社
CS234 斯坦福强化学习课程

