【LeetCode 343】整数拆分——Python解决
1. 题目描述
给定一个正整数 n,将其拆分为至少两个正整数的和,并使这些整数的乘积最大化。 返回你可以获得的最大乘积。
示例 1:
输入: 2
输出: 1
解释: 2 = 1 + 1, 1 × 1 = 1。
示例 2:
输入: 10
输出: 36
解释: 10 = 3 + 3 + 4, 3 × 3 × 4 = 36。
说明: 你可以假设 n 不小于 2 且不大于 58。
2. 分析
将正整数分割成几份,这个是未知的,所以很难用循环去解决,因为不知道要做几重循环,这种情况通常要使用递归,也就是暴力解法:回溯遍历将一个数做分割的所有可能性,时间复杂度为 O(2^n),但是容易产生重复子问题,如下图所示:
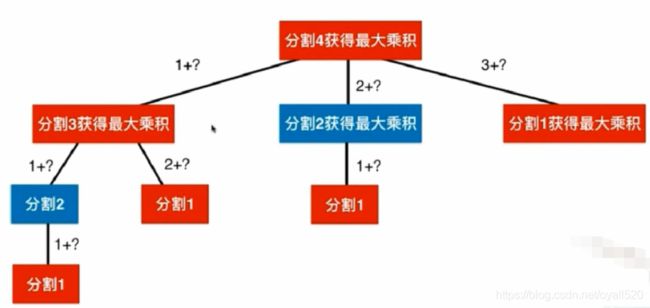

所以在此基础上可以用自顶向下的记忆化搜索或者自底向上的动态规划
3. 第一种方法——记忆化搜索
- 首先是递归的终止条件:若传进来的数字是1,那么这个数字是无法分割的,直接return 1就好了;
- 接下来的情况都可以对n进行分割,那么我们就要遍历所有分割的可能性,这样每次都能将n分割成 i+(n-i) 这样的两个数字,所获得的乘积是 i*backtrack(n-i),我们要做的就是在这样一个个乘积中获取一个最大值,所以我们要初始化一个变量 res = float(’-inf’),在循环中每一次
res = max(res, i * backtrack(n-i));
此处要注意一个陷阱:backtrack()这个函数的定义是至少要将n-i分割成两部分,可是当我们具体分割n时,就将n分割成 i和n-i 也是可以的,因此在取max时还需添加一个i*(n-i):res = max(res, i*(n-i), i*backtrack(n-i))。也就是说对n分割成 i 和 n-i,(1)是不继续分割n-i了,直接看i*(n-i)哪一个最大;(2)是继续分割n-i,看能否找到一个分割后的结果与i的乘积最大。
但是上面这样写同样包含重叠子问题,重叠的部分就在于backtrack(n-i)部分,所以我们设置一个变量memo来具体的记录出现的结果,初始化为memo = [-1 for i in range(n+1)]:
- 在递归函数backtrack中,若n=1,直接返回-1;
- 否则就要看memo[n]这个值是否进行了计算,若
memo[n] != -1,也就表明memo[n]之前计算过,直接返回memo[n]即可; - 否则就要进行下面的逻辑运算,逻辑运算过后要将 res 的值赋给memo[n](
memo[n] = res),表示对这一次计算的结果进行了记录,再把res返回即可。
——这就是记忆化搜索。保险起见,在主函数里运用assert,保证传进来的数字是大于等于2的 assert (n >=2),因为至少要分割成两部分,2是最小的可以分割成两部分的数字。
class Solution:
def integerBreak(self, n: int) -> int:
assert(n >= 2)
self.memo = [-1 for i in range(n + 1)]
return self.backtrack(n)
def backtrack(self, n):
if n == 1:
return 1
if self.memo[n] != -1:
return self.memo[n]
res = float('-inf')
for i in range(1, n):
res = max(res, i*(n-i), i*self.backtrack(n-i))
self.memo[n] = res
return res
4. 第二种方法——动态规划
在主函数中进行assert之后依然要创建一个记忆的数组memo,memo = [-1 for i in range(n+1)](表示memo有n+1个元素,每个元素的初始值为-1),memo[i]表示将数字i分割(至少分割成两部分)后得到的最大乘积。
使用动态规划是自底向上解决问题:
- 首先对底的情况进行设置:memo[1]=1,
- 接下来就可以一步步的循环求解memo[i]:
for i in range(2, n+1),具体求解的方式依然是再进行一次循环,这次循环是尝试将i这个数字进行分割:for j in range(1, i),也就是说每次都尝试将 i 这个数字分割成 j + (i - j)这样的两部分——对于这样的分割,背后的乘积依然是:(1)就是 j * (i-j),(2)就是将 i-j 继续分割得到 j * memo[i-j],因为 i-j 一定小于i,所以此时 memo[i-j] 一定已经被计算出来了,此处就可以被使用。 - j * (i-j)和 j * memo[i-j]是得到的两个备选项,和已经有的memo[i]取最大值,把结果赋给memo[i]即可:
memo[i] = max(memo[i], j * (i-j), j * memo[i-j]),最终只需要返回memo[n]即可。
class Solution:
def integerBreak(self, n: int) -> int:
assert(n >= 2)
memo = [-1 for i in range(n + 1)]
if n == 1:
return 1
for i in range(2, n + 1):
for j in range(1, i):
memo[i] = max(memo[i], j*(i-j), j*memo[i-j])
return memo[n]
注意:
记忆化搜索和动态规划的for循环起始值的差别:
# 记忆化搜索
for i in range(1, n):
res = max(res, i*(n-i), i*self.backtrack(n-i))
记忆化搜索 i 的起始值从1开始,是因为要将 n 分割成 (n-1)+1、(n-2)+2……这些情况,然后再对n-1、n-2……这部分进行分割,若 i 从2开始, 就会漏了 (n-1)+1 这种情况,结果会出错。
# 动态规划
for i in range(2, n + 1):
for j in range(1, i):
memo[i] = max(memo[i], j*(i-j), j*memo[i-j])
动态规划的外层循环 i 的起始值从2开始,是因为此处求解的是memo[n],而memo[1]的值已经知晓是为1,所以自然要从2开始;内循环是具体的分割部分,还是从1开始。