【NP】numpy(3) 多维下标存取&函数库
导航
- 前文链接
- 整数数组作为下标
- N s = 0 N_s=0 Ns=0
- N s ≠ 0 N_s\neq 0 Ns=0
- 函数库
- 随机数
- 排列组合和抽样
- 统计计算
- 极值和排序
前文链接
numpy(2)
整数数组作为下标
设整数数组有 N t N_t Nt个,而切片有 N s N_s Ns个, N t + N s N_t+N_s Nt+Ns是数组的维数D. 这 N t N_t Nt个整数数组必须满足广播条件,假设进行广播之后的维数是 M M M,形状为 ( d 0 , d 1 , … , d M − 1 ) (d_0, d_1, \dots, d_{M-1}) (d0,d1,…,dM−1).
N s = 0 N_s=0 Ns=0
当不存在切片元素时,下标得到数组的shape和数组广播之后的shape相同. 每个元素通过以下公式获得.
R [ i 0 , i 1 , … , i M − 1 ] = X [ i n d 0 [ i 0 , i 1 , … , i M − 1 ] , … , i n d N t − 1 [ i 0 , i 1 , … , i M − 1 ] R[i_0, i_1, \dots, i_{M-1}]=X[ind_0[i_0, i_1, \dots, i_{M-1}], \dots, ind_{N_t-1}[i_0, i_1, \dots, i_{M-1}] R[i0,i1,…,iM−1]=X[ind0[i0,i1,…,iM−1],…,indNt−1[i0,i1,…,iM−1]
import numpy as np
a=np.arange(3*4*5).reshape(3, 4, 5)
i0=np.array([[1, 2, 1], [0, 1, 0]])
i1=np.array([[[0]], [[1]]])
i2=np.array([[[2, 3, 2]]])
b=a[i0, i1, i2]
print(b)
# 使用broadcast_arrays()查看广播后的数组
ind0, ind1, ind2=np.broadcast_arrays(i0, i1, i2)
print(ind0)
print(ind1)
print(ind2)
# 验证对应关系
i, j, k=0, 1, 2
print(b[i, j, k])
print(a[ind0[i, j, k], ind1[i, j, k], ind2[i, j, k]])
N s ≠ 0 N_s\neq 0 Ns=0
下标元组整数数组之间不存在切片,整数数组只有一个或连续多个整数数组.
import numpy as np
a=np.arange(3*4*5).reshape(3, 4, 5)
i0=np.array([[1, 2, 1], [0, 1, 0]])
i1=np.array([[[0]], [[1]]])
i2=np.array([[[2, 3, 2]]])
c=a[1:3, i0, i1]
print(c.shape) # (2, 2, 2, 3)
ind0, ind1 = np.broadcast_arrays(i0, i1)
print(ind0.shape) # (2, 2, 3)
下标元组中的整数不连续时,结果数组的shape属性为整数数组广播之后形状后面加上切片元素所对应的形状.
import numpy as np
a=np.arange(3*4*5).reshape(3, 4, 5)
i0=np.array([[1, 2, 1], [0, 1, 0]])
i1=np.array([[[0]], [[1]]])
i2=np.array([[[2, 3, 2]]])
d=a[i0, :, i1]
print(d.shape) # (2, 2, 3, 4)
ind0, ind1 = np.broadcast_arrays(i0, i1)
i, j, k=1, 1, 2
print(d[i, j, k]==a[ind0[i, j, k],:,ind1[i, j, k]]) # [True]
函数库
np.random函数库
随机数
np.random模块提供了如下产生随机数的函数
| 函数 | 功能 |
|---|---|
rand() |
产生0到1之间的随机浮点数,参数指定产生数组的形状 |
randn() |
产生标准正态分布的随机数,参数含义与randn()相同 |
randint() |
产生指定范围的随机整数 |
import numpy as np
from numpy import random as rd
np.set_printoptions(precision=2) # 设置显示精度
r1=rd.rand(4, 3)
r2=rd.randn(4, 3)
r3=rd.randint(0, 10, (4, 3))
print(r1)
print(r2)
print(r3)
可以产生符合特定分布的随机数的函数,使用size参数指定数组的形状
| 函数名 | 功能 |
|---|---|
normal(loc, scale, size) |
正态分布,前两个参数为均值和标准差 |
uniform(low, high, size) |
均匀分布,前两个参数指定区间的起始值和终点值 |
poisson(lam, size) |
泊松分布,第一个参数为 λ \lambda λ,表示事件的发生强度 |
import numpy as np
from numpy import random as rd
np.set_printoptions(precision=2) # 设置显示精度
r1=rd.normal(1, 2, (4, 3))
r2=rd.uniform(0, 10, (4, 3))
r3=rd.poisson(2.0, (4, 3))
print(r1)
print(r2)
print(r3)
排列组合和抽样
| 函数 | 功能 |
|---|---|
permutation() |
产生一个乱序数组,当参数为n,返回 [ 0 , n ) [0, n) [0,n)这 n n n个数的随机排列,当参数为一个序列时,返回该序列的一个随机排列 |
shuffle() |
将参数序列的顺序打乱 |
choice() |
从指定样本中进行随机抽取,size指定输出数组的形状;replace为True时,进行重复抽样,False为无放回采样,默认值为True;p指定每个元素被抽取对应的概率,默认为等概率. |
import numpy as np
from numpy import random as rd
np.set_printoptions(precision=2) # 设置显示精度
a=np.arange(1, 25, dtype=float)
c1=rd.choice(a, size=(3, 4))
c2=rd.choice(a, size=(3, 4), replace=False)
c3=rd.choice(a, size=(3, 4), p=a/np.sum(a)
print(c1)
print(c2)
print(c3)
统计计算
std()和var()分别计算数组的标准差和方差,方差有偏样本方差(biased sample variance)和无偏样本方差(unbiased sample variance)两种
偏样本方差:
s n 2 = 1 n ∑ i = 1 n ( x i − x ˉ ) 2 s_n^2=\frac{1}{n}\sum_{i=1}^n(x_i-\bar{x})^2 sn2=n1i=1∑n(xi−xˉ)2
无偏样本方差:
s 2 = 1 n − 1 ∑ i = 1 n ( x i − x ˉ ) 2 s^2=\frac{1}{n-1}\sum_{i=1}^{n}(x_i-\bar{x})^2 s2=n−11i=1∑n(xi−xˉ)2
当参数ddof=0时,表示计算偏样本方差,当ddof=1时,表示计算无偏样本方差,默认值设置为0.
偏样本方差是是最大似然估计(MLE)的参数估计结果,假设对正态分布 N ( μ , σ 2 ) \mathcal{N}(\mu, \sigma^2) N(μ,σ2)进行MLE.
N ( μ , σ 2 ) \mathcal{N}(\mu, \sigma^2) N(μ,σ2)的pdf如下
f ( x ∣ μ , σ 2 ) = 1 2 π σ 2 e − ( x − μ ) 2 2 σ 2 f(x\mid \mu, \sigma^2)=\frac{1}{\sqrt{2\pi\sigma^2}}e^{-\frac{(x-\mu)^2}{2\sigma^2}} f(x∣μ,σ2)=2πσ21e−2σ2(x−μ)2
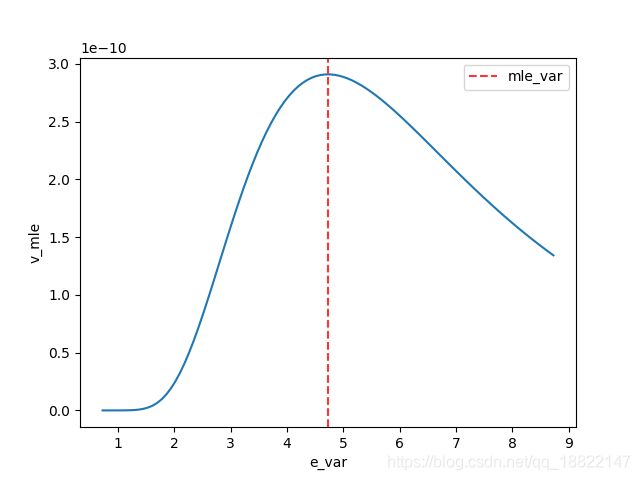
找到一组参数 ( μ , σ 2 ) (\mu, \sigma^2) (μ,σ2)使得以下方程结果最大
f ( x 1 ) f ( x 2 ) … f ( x n ) f(x_1)f(x_2)\dots f(x_n) f(x1)f(x2)…f(xn)
import numpy as np
from numpy import random as rd
import matplotlib.pyplot as plt
np.set_printoptions(precision=2) # 设置显示精度
def normal_pdf(mean, var, x):
return 1/np.sqrt(2*np.pi*var)*np.exp(-(x-mean)**2/(2*var))
def demo():
rd.seed(29)
# 真实数据
data=rd.normal(loc=0, scale=2.0, size=10)
# 计算偏样本方差
mean, var=np.mean(data), np.var(data, ddof=0)
var_rng=np.linspace(max(var-4, 0.1), var+4, 100)
p=normal_pdf(mean, var_rng.reshape(-1, 1), data) # broadcast
p=np.product(p, axis=1)
plt.plot(var_rng, p)
plt.axvline(var, 0, 1, color='red', linestyle='--', alpha=0.8, label='mle_var')
plt.xlabel('e_var')
plt.ylabel('v_mle')
plt.legend()
plt.show()
demo()
极值和排序
| 函数名 | 功能 |
|---|---|
sort() |
返回排序后的新数组,默认axis=-1,np.sort(a)对行值进行排序,np.sort(a, axis=0)对列值进行排序 |
argsort() |
返回数组的排序下标,默认axis=-1 |
minimum()&maximum() |
比较两个数组对应下标的元素,返回数组形状为两参数数组广播之后的形状. |
argmax()&argmin() |
求出最大值和最小值的下标 |
import numpy as np
from numpy import random as rd
import matplotlib.pyplot as plt
np.set_printoptions(precision=2) # 设置显示精度
a=np.array([1, 3, 5, 7])
b=np.array([2, 4, 6])
print(np.maximum(a.reshape(1, -1), b.reshape(-1, 1)))
使用sort_axis()可以进行关联数组排序
import numpy as np
from numpy import random as rd
import matplotlib.pyplot as plt
np.set_printoptions(precision=2) # 设置显示精度
def demo():
rd.seed(29)
a=rd.randint(0, 10, size=(4, 5))
sort_axis1=np.argsort(a) # 行排序下标
sort_axis0=np.argsort(a, axis=0) # 列排序下标
axis0, axis1=np.ogrid[:a.shape[0], :a.shape[1]]
print(a[axis0, sort_axis1])
print(np.sort(a))
demo()