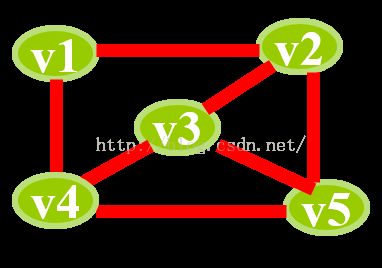
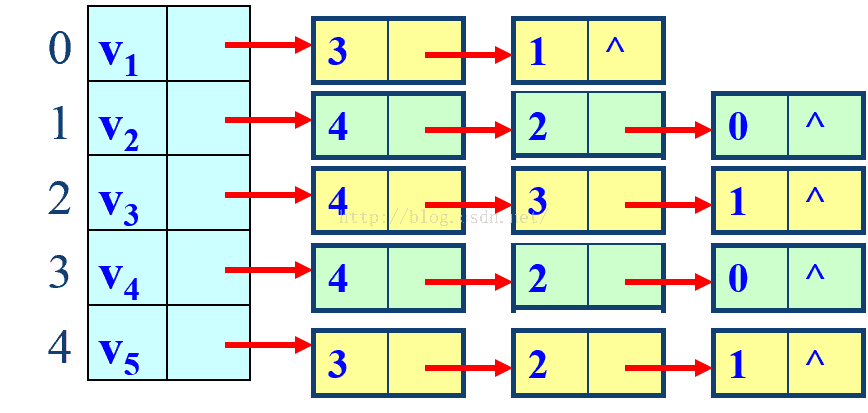
数据结构上机实验--有向图邻接表的建立,深度广度搜索及拓扑排序
1、以邻接表存储方式创建一个有向图,并对图进行深度遍历和广度遍历。
2、编写程序实现图的拓扑排序。
邻接表的存储表示
#defineMVNum 100 //最大顶点数
typedefstructArcNode{ //边结点
intadjvex; //该边所指向的顶点的位置
structArcNode *nextarc; //指向下一条边的指针
OtherInfo info; //和边相关的信息
}ArcNode;
typedefstructVNode{
VerTexType data; //顶点信息
ArcNode *firstarc; //指向第一条依附该顶点的边的指针
}VNode,AdjList[MVNum]; //AdjList表示邻接表类型
typedefstruct{
AdjList vertices; //邻接表
intvexnum,arcnum; //图的当前顶点数和边数
}ALGraph;
拓扑排序
对一个有向无环图(Directed Acyclic Graph简称DAG)G进行拓扑排序,是将G中所有顶点排成一个线性序列,使得图中任意一对顶点u和v,若边(u,v)∈E(G),则u在线性序列中出现在v之前。通常,这样的线性序列称为满足拓扑次序(Topological Order)的序列,简称拓扑序列。简单的说,由某个集合上的一个偏序得到该集合上的一个全序,这个操作称之为拓扑排序
//If you are student of HPU.
//Maybe you will be surprised.
//You can find easily the answer.
//Because I will tell you,don't be too complacent.
//Whatever you're good at.
//Everytime,you only just a green hand.
//By Cooperative Program at Undergraduate Level in Computer Science & technology
//1404
//I'm Oliver Queen.
#include
#include
#include
#include
#include
using namespace std;
#define MaxVertexNum 100
typedef char VertexType;
typedef struct node //边表节点
{
int adjvex;
node* next;
}EdgeNode;
typedef struct //顶点表节点
{
VertexType data;
EdgeNode *firstedge;
}VertexNode;
typedef VertexNode AdjList[MaxVertexNum];
typedef struct
{
AdjList adjlist;
int vexum,arcnum;//顶点数和边数
}ALGraph;
int per[100000];//用于记录各个节点的入度情况
int LocateVex(ALGraph G , VertexType v){//确定点v在G中的位置
for(int i = 0; i < G.vexum; ++i)
if(G.adjlist[i].data == v)
return i;
return -1;
}
void find(ALGraph g,char xx,int nnn)
{
for(int i=0;i>g.adjlist[i].data;
g.adjlist[i].firstedge=NULL;
}
printf("\n");
printf("请输入有向图之间的依附关系(如a b)\n");
for(k=0;k>v1>>v2;
find(g,v2,g.vexum);
int aa,bb;
aa = LocateVex(g, v1); bb = LocateVex(g, v2);
EdgeNode *pp;
pp=new EdgeNode;
pp->adjvex=bb;
pp->next=g.adjlist[aa].firstedge;//插入头部
g.adjlist[aa].firstedge=pp;
}
}
bool visited[100000];
void DFS(ALGraph G, int v){ //图G为邻接表类型,数v代表出发点
cout << G.adjlist[v].data << " ";
visited[v] = true; //访问第v个顶点,并置访问标志数组相应分量值为true
EdgeNode *p = G.adjlist[v].firstedge; //p指向v的边链表的第一个边结点
while(p != NULL){ //边结点非空
int w = p->adjvex; //表示w是v的邻接点
if(!visited[w]) DFS(G, w); //如果w未访问,则递归调用DFS
p = p->next; //p指向下一个边结点
}
}//DFS
void BFS(ALGraph G, int v){
EdgeNode *p;
int queue[100000],front=0,rear=0;
int j;
cout << G.adjlist[v].data << " ";
visited[v] = true;
rear++;
queue[rear]=v;
while(front!=rear)
{
front++;
j=queue[front];
p=G.adjlist[j].firstedge;
while(p!=NULL)
{
if(visited[p->adjvex]==0)
{
cout << G.adjlist[p->adjvex].data << " ";
visited[p->adjvex]=true;
rear++;
queue[rear]=p->adjvex;
}
p=p->next;
}
}
}
char mm[100000];//记录拓扑排序的最终结果
bool TUOPU(ALGraph G)
{
int i;
int ji=0;
stack cc;
for(i=0;inext)
{
int k=p->adjvex;
if(!(--per[k]))
cc.push(k);
}
}
if(count";
cout << p1->adjvex;
p1 = p1->next;
}
printf("\n");
}
}
memset(visited,false,sizeof(visited));
printf("\n");
printf("进行邻接表的正式的深搜和广搜\n");
printf("\n");
int xx;
printf("请输入起始位置的数组下标:");
scanf("%d",&xx);
printf("*****深搜结果*****\n");
DFS(p,xx);
printf("\n");
memset(visited,false,sizeof(visited));
printf("*****广搜结果*****\n");
BFS(p,xx);
printf("\n");
printf("\n*****开始进行拓扑排序*****\n");
printf("\n");
printf("输出每个节点的入度情况\n");
for(int i=0;i