二分和排序

快速排序

算法思想

• 基于分治
• 总体步骤的话
  • 确定分界点
  • 调整分区
  • 递归

步骤

1、x = q[l + r >> 1],i = l - 1,j = r + 1; （i = l-1，j = r+1。是因为下面，do i++，先加了再说。所以这里。先把其移动到l,r的两侧）

2、分治（小于x的放到左边，大于x的放到右边）。
3、分别递归左右两边。

模板

void quick_sort(int q[], int l, int r)
{
    if (l >= r) return; //区间没数或者只有一个数

    int i = l - 1, j = r + 1, x = q[l + r >> 1];  // i = l-1，j = r+1。是因为下面，do i++
    //先加了再说。所以这里。先把其移动到l,r的两侧
    while (i < j)// 如果i和j 没有穿越和重合时候，才能继续。
    {
        do i ++ ; while (q[i] < x); //左边不符合条件
        do j -- ; while (q[j] > x); //右边不符合条件的
        if (i < j) swap(q[i], q[j]);// 如果i和j 没有穿越和重合时候，才能继续。重合就不用交换了。
    }
    quick_sort(q, l, j), quick_sort(q, j + 1, r);
}

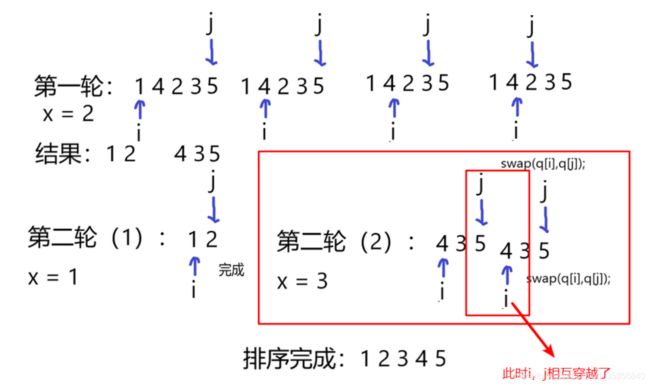
快速排序的结果

将区间划分为两端。

• 左段 <= target
• 右段 >= target

需要注意的点

• 为什么递归两个区间为（l,j） 和（j+1,r）？
• 为什么i = l - 1,j = r + 1？

第一个问题：为什么递归两个区间为 （l,j） 和（j+1,r）？

• 因为i和j相互穿越了

再比如：

第二个问题：为什么i = l - 1,j = r + 1？

i = l-1，j = r+1。是因为下面，do i++，先加了再说。所以这里。先把其移动到l,r的两侧）

归并排序

算法思想

• 思想还是分治
• 步骤为三步和 快排类似
  • 分界点为 mid
  • 递归，分化为两段
  • 归并，合二为一

步骤

• 区间一分为二。
• 递归左右，使得左右归并排序
• 最后合二为一

模板

void msort(int q[],int l,int r)
{
    if(l>=r) return ;//当两个指针重合的时候就不用再排了

    int mid=(l+r)/2;//分界点是中间

    msort(q,l,mid);//排序左半边
    msort(q,mid+1,r);//排序右半边

    int k=0;
    int i=l,j=mid+1;//两个指针分别指向左半边和右半边的开头

    while(i<=mid && j<=r)
    {
        if(q[i]<=q[j])
        {
            res[k++]=q[i++];
        }
        else
        {
            res[k++]=q[j++];
        }
    }//合二为一（归并）

    while(i<=mid) res[k++]=q[i++];
    while(j<=r) res[k++]=q[j++];
    //把剩下的那一段放到res里面去

    i=l,k=0;//再分别指向q和res的开头位置
    while(i<=r)
    {
        q[i]=res[k];//再把临时的res放回最后的q里面去
        i++,k++;
    }
}

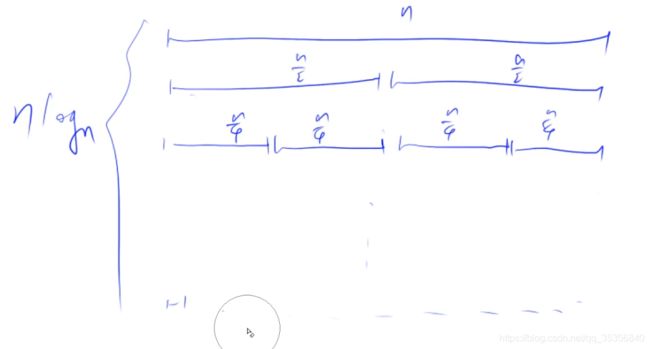
算法截图

时间复杂度是 O(nlogn)

整数二分

作用为：利用二分搜索的思想。来找到一个数的左右边界。

例如： {1，2，2，4，4，8，10}

找到值为2的左边界序号为2，右边界序号3。如何找到左右边界呢

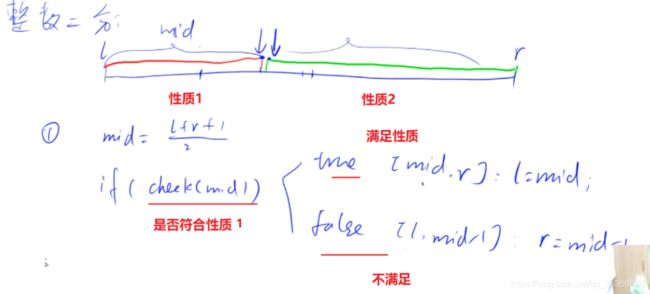
步骤

算法截图

左右边界不一样。左加右不加

模板

bool check(int x) {/* ... */} // 检查x是否满足某种性质

// 查找左边界
//查找大于等于/大于key的第一个元素
int bsearch_1(int l, int r)
{
    while (l < r)
    {
        int mid = l + r >> 1;
        if (check(mid)) r = mid;    // check()判断mid是否满足性质
        else l = mid + 1;
    }
    return l;
}
// 查找右边界
//查找小于等于/小于key的最后一个元素
int bsearch_2(int l, int r)
{
    while (l < r)
    {
        int mid = l + r + 1 >> 1;
        if (check(mid)) l = mid;
        else r = mid - 1;
    }
    return l;
}

浮点数二分

• 不用考虑边界。
• 循环条件终止有两个
  • 循环100次。相当于 / 2^n
  • r - l > eps // eps 表示精度，取决于题目对精度的要求

模板

bool check(double x) {/* ... */} // 检查x是否满足某种性质

double bsearch_3(double l, double r)
{
    const double eps = 1e-6;   // eps 表示精度，取决于题目对精度的要求
    while (r - l > eps)
    {
        double mid = (l + r) / 2;
        if (check(mid)) r = mid;
        else l = mid;
    }
    return l;
}

或者

bool check(double x) {/* ... */} // 检查x是否满足某种性质

double bsearch_3(double l, double r)
{
    const double eps = 1e-6;   // eps 表示精度，取决于题目对精度的要求
    for(int i = 1; i<= 100 ; i++)
    {
        double mid = (l + r) / 2;
        if (check(mid)) r = mid;
        else l = mid;
    }
    return l;
}