线性规划--最小费用最大流
假期 2020.01.24
题目描述
在网络布线的工程中,有许多电缆,而电缆的粗细不同,流量与费用也不一样,那么如何安排才能获得费用最小且流量最大的网络呢?
思路分析
因为要满足两个条件,那么我们可从两大方面入手:
- 费用最小,我们可以先找到费用最小的网路线,然后在该路径上面增加流量到最大值即可。
- 也可以先寻找最大流量,然后找负值的圈,因为这样子可以在一定程度上减少费用,直到减少到最小即可,即不再存在无关的负值圈,都是剩下的必要的路径了。
算法分析
- 存储结构:
int expense_choice[Max_size], pre_choice[Max_size];//最短距离,前驱
int visited[Max_size],visited_count[Max_size];//标记访问数组,入队次数
int max_flow;//最大流
int num;//编号
struct Vertex {//邻接表头节点
int first;
}vertex[Max_size];
struct Edge {
int start,next;//弧尾,下一条邻接边
int contain, flow, expense;//边的最大容量,边的流量,边的花费
}edge[Max_size];
- 初始化,其中添加边的时候,是添加双向边,输入时需要注意,主体流向都是从顶点小的编号指向顶点大的编号的边,否则输出结果不正确,因为,我们要确定一个流向。
memset(vertex, -1, sizeof(vertex));//邻接表表头初始化为-1
cout << "请输入两个节点(v,w)和两者之间的容量与花费(每项共4个数据):" << endl;
for (int i = 1; i <= edge_count; i++)
{
cin >> v >> w >> we >> e;
add(v, w, we, e);
}
cout << endl;
max_flow = 0;
num = 0;
添加边,num作为全部边的编号,从0开始
void add_edge(int v, int w, int we, int e)//加边,赋值
{
edge[num].start = w;//弧头
edge[num].contain = we;//容量
edge[num].expense = e;//花费
edge[num].flow = 0;//流量
edge[num].next = vertex[v].first;//下一条边序号
vertex[v].first = num ++;//边的序号编号
return ;
}
- int Search_flow(int vertex_count);//寻找路径函数;仍然利用bfs算法实现,其中判断条件是该边的容量仍然大于当前的流量值,并且当当前这条弧的弧头的花费存在更优值,就更新到该点的花费并该点入队。
而判断负值圈的意义在于,因为存在负值边,而我们所求的是最小值,那么因为存在负值边,会使程序在此处循环无解。注意前驱数组存的是每一个顶点的前面一条弧的编号,而不是顶点编号。
if (edge[i].contain > edge[i].flow && expense_choice[cur] > expense_choice[temp] + edge[i].expense)//存在可行解
{
expense_choice[cur] = expense_choice[temp] + edge[i].expense;//更新到cur点的花费值
pre_choice[cur] = i;//cur的前驱更新
if (visited[cur] == 0)
{
visited_count[cur]++;//访问次数增加一
q.push(cur);//入队
visited[cur] = 1;//标记
if (visited_count[cur] > vertex_count)//存在负环
return 0;
}
}
- int best_expaflo(int i, int vertex_count);//处理路径函数;其中使用i^1(或 i + 1) 的目的是因为我们在存储的时候采取的是正向为i,那么逆向是i+1,,因此利用这个特点就可以知道某边的两个顶点编号。
for (i = pre_choice[vertex_count]; i != -1; i = pre_choice[edge[i ^ 1].start])//使用i^1的目的是因为我们在存储的时候采取的是正向为i,那么逆向是i+1
{
current_cost = min(current_cost, edge[i].contain - edge[i].flow);
cout << "--" << edge[i ^ 1].start;
}
代码解析
#include测试数据
6
10
1 3 4 7
1 2 3 1
2 5 4 5
2 4 6 4
2 3 1 1
3 5 3 6
3 4 5 3
4 6 7 6
5 6 3 2
5 4 3 3
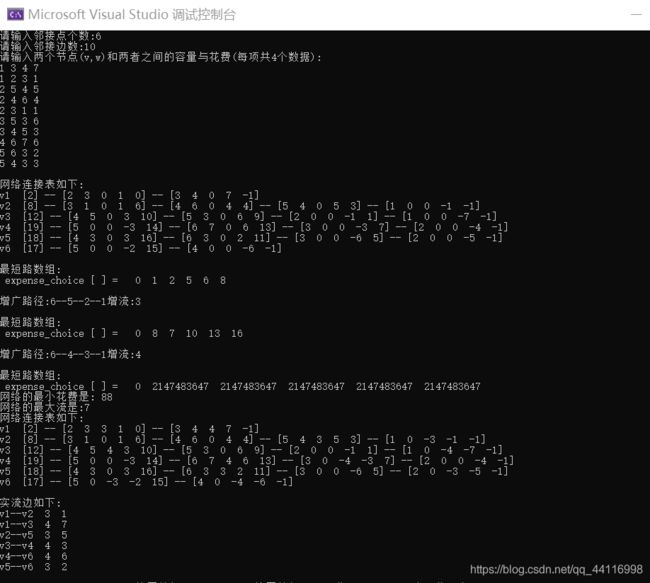
运行结果
参考
实现借鉴《趣学算法》