2016中国大学生程序设计竞赛 - 网络选拔赛题解报告
此文章可以使用目录功能哟↑(点击上方[+])
好弱呀,感觉要打铁...
链接→2016中国大学生程序设计竞赛 - 网络选拔赛
 Problem 1001 A water problem
Problem 1001 A water problem
Accept: 0 Submit: 0
Time Limit: 5000/2500 MS (Java/Others) Memory Limit : 65536/65536 K (Java/Others)
 Problem Description
Problem Description
Two planets named Haha and Xixi in the universe and they were created with the universe beginning.
There is 73 days in Xixi a year and 137 days in Haha a year.
Now you know the days N after Big Bang, you need to answer whether it is the first day in a year about the two planets.
 Input
Input
There are several test cases(about 5 huge test cases).
For each test, we have a line with an only integer N(0≤N), the length of N is up to 10000000.
 Output
Output
For the i-th test case, output Case #i: , then output "YES" or "NO" for the answer.
 Sample Input
Sample Input
0
333
 Sample Output
Sample Output
Case #2: YES
Case #3: NO
 Problem Idea
Problem Idea
解题思路:
【题意】
两个星球从宇宙大爆炸开始就产生了
Xixi星球一年有73天,Haha星球一年有137天
问宇宙大爆炸开始第N天是否是两个星球一年当中的第一天
【类型】
同余定理
【分析】
认真读题,我们可以发现如果第N天是两个星球一年当中的第一天
那么N必定能被73整除,同时能被137整除
就这样,题目发生了转变,然而此题还没有就此解决
因为N这个数长度可达10000000,显然这是个极大的数
那我们就需要采取同余定理求解
首先,我们知道模运算是不影响乘法和加法的
所以一个数,比如23,对5取模,23≡2*10+3(mod 5)
故,这个巨大的数N可以拆解成一位一位取模,这样,此题就可以得到圆满解决
【时间复杂度&&优化】
O(strlen(n))
题目链接→HDU 5832 A water problem
 Source Code
Source Code
/*Sherlock and Watson and Adler*/
#pragma comment(linker, "/STACK:1024000000,1024000000")
#include
#include
#include
#include
#include
#include
#include
#include  Problem 1002 Zhu and 772002
Problem 1002 Zhu and 772002
Accept: 0 Submit: 0
Time Limit: 2000/1000 MS (Java/Others) Memory Limit : 65536/65536 K (Java/Others)
 Problem Description
Problem Description
Zhu and 772002 are both good at math. One day, Zhu wants to test the ability of 772002, so he asks 772002 to solve a math problem.
But 772002 has a appointment with his girl friend. So 772002 gives this problem to you.
There are n numbers a1,a2,...,an. The value of the prime factors of each number does not exceed 2000, you can choose at least one number and multiply them, then you can get a number b.
How many different ways of choices can make b is a perfect square number. The answer maybe too large, so you should output the answer modulo by 1000000007.
 Input
Input
First line is a positive integer T , represents there are T test cases.
For each test case:
First line includes a number n(1≤n≤300),next line there are n numbers a1,a2,...,an,(1≤ai≤10^18).
 Output
Output
For the i-th test case , first output Case #i: in a single line.
Then output the answer of i-th test case modulo by 1000000007.
 Sample Input
Sample Input
3
3 3 4
3
2 2 2
 Sample Output
Sample Output
3
Case #2:
3
 Problem Idea
Problem Idea
解题思路:
【题意】
有n个数,每个数的质因数不会超过2000
问从n个数中至少选取1个数,它们的乘积是完全平方数的情况有多少种,结果对1000000007取模
【类型】
高斯消元
【分析】
首先,我们知道的是,完全平方数的各种质因子必定出现偶数次
不然不可能被开方
例如36=2*2*3*3
质因子2,3均出现两次
所以呢,此题已经可以转化为类似开关问题的高斯消元了
这里,![]() ,表示第i个数取或不取
,表示第i个数取或不取
![]() ,表示质因子出现偶数次
,表示质因子出现偶数次
![]() ,表示(第j个数分解质因数后,2000以内第i个质数出现多少次,奇数次值为1,偶数次值为2)
,表示(第j个数分解质因数后,2000以内第i个质数出现多少次,奇数次值为1,偶数次值为2)
剩下的就是套一下高斯消元的模板,求解出自由变元的个数ans,那此题的结果就是![]() ,这个快速幂求解一下就可以了
,这个快速幂求解一下就可以了
如果还是不明白的话,我们来举例说明
就比如样例3,3,4
方程变元x前的系数k为我们打素数表2,3,5,……,1999中第k个质数出现奇数次还是偶数次
那该样例可得方程组为
第一条方程是质数2的贡献,因为3是不包含质因子2的,故贡献为0,而4虽包含质因子2,但出现了偶数次,故贡献同样为0
第二条方程,两个3都贡献了1,而4不包含质因子3,所以无贡献
显然,方程组只有一条方程,但有3个未知数,所以自由变元有2个,而自由变元的取值为{0,1}
故方程组的解有2^2=4种,除去全为0的一种(因为题目指明至少取一个数),剩3种(1,1,0),(0,0,1),(1,1,1)
【时间复杂度&&优化】
O(n^3)
题目链接→HDU 5833 Zhu and 772002
 Source Code
Source Code
/*Sherlock and Watson and Adler*/
#pragma comment(linker, "/STACK:1024000000,1024000000")
#include
#include
#include
#include
#include
#include
#include
#include  Problem 1004 Danganronpa
Problem 1004 Danganronpa
Accept: 0 Submit: 0
Time Limit: 2000/1000 MS (Java/Others) Memory Limit : 65536/65536 K (Java/Others)
 Problem Description
Problem Description
Chisa Yukizome works as a teacher in the school. She prepares many gifts, which consist of n kinds with a[i] quantities of each kind, for her students and wants to hold a class meeting. Because of the busy work, she gives her gifts to the monitor, Chiaki Nanami. Due to the strange design of the school, the students' desks are in a row. Chiaki Nanami wants to arrange gifts like this:
1. Each table will be prepared for a mysterious gift and an ordinary gift.
2. In order to reflect the Chisa Yukizome's generosity, the kinds of the ordinary gift on the adjacent table must be different.
3. There are no limits for the mysterious gift.
4. The gift must be placed continuously.
She wants to know how many students can get gifts in accordance with her idea at most (Suppose the number of students are infinite). As the most important people of her, you are easy to solve it, aren't you?
 Input
Input
The first line of input contains an integer T(T≤10) indicating the number of test cases.
Each case contains one integer n. The next line contains n (1≤n≤10) numbers: a1,a2,...,an, (1≤ai≤100000).
 Output
Output
For each test case, output one line containing “Case #x: y” (without quotes) , where x is the test case number (starting from 1) and y is the answer of Chiaki Nanami's question.
 Sample Input
Sample Input
2
3 2
 Sample Output
Sample Output
 Problem Idea
Problem Idea
解题思路:
【题意】
n种礼物,每种有a[i]个,所有的礼物可以作为普通礼物,也可以作为神秘礼物发放给孩子
现在从第一个人开始,每人可以收到一个普通礼物和一个神秘礼物,相邻两个人不能收到相同的普通礼物,神秘礼物没限制,发完为止
问最多有多少个人可以拿到两件礼物
【类型】
贪心
【分析】
暂时先不考虑普通礼物的限制
那么最多有sum/2个人可以拿到两件礼物(sum为总的礼物件数,即a[1]+a[2]+……+a[n])
那么在考虑普通礼物限制的情况下,我们肯定先要发放普通礼物,直到不能发或超过sum/2为止,这时多出来的礼物就作为神秘礼物补齐发到过普通礼物的孩子
那么说明情况是不能发呢?因为相邻两人要获得不同的普通礼物
所以我们可以借助优先队列,每次将队首的两种礼物取出来发放
假设队首两种礼物的数量为a,b(a>b)
那么可以有2*b个孩子拿到普通礼物,没发完的第一种礼物还剩a-b件,丢进优先队列重新来过
最终得到答案ans,与sum/2取个小值就行了
【时间复杂度&&优化】
O(n)
题目链接→HDU 5835 Danganronpa
 Source Code
Source Code
/*Sherlock and Watson and Adler*/
#pragma comment(linker, "/STACK:1024000000,1024000000")
#include
#include
#include
#include
#include
#include
#include
#include  Problem 1008 Special Tetrahedron
Problem 1008 Special Tetrahedron
Accept: 0 Submit: 0
Time Limit: 4000/2000 MS (Java/Others) Memory Limit : 65536/65536 K (Java/Others)
 Problem Description
Problem Description
Given n points which are in three-dimensional space(without repetition).
Please find out how many distinct Special Tetrahedron among them. A tetrahedron is called Special Tetrahedron if it has two following characters.
1. At least four edges have the same length.
2. If it has exactly four edges of the same length, the other two edges are not adjacent.
 Input
Input
Intput contains multiple test cases.
The first line is an integer T,1≤T≤20, the number of test cases.
Each case begins with an integer n(n≤200), indicating the number of the points.
The next n lines contains three integers xi,yi,zi, (−2000≤xi,yi,zi≤2000), representing the coordinates of the ith point.
 Output
Output
For each test case,output a line which contains"Case #x: y",x represents the xth test(starting from one),y is the number of Special Tetrahedron.
 Sample Input
Sample Input
4
0 0 0
0 1 1
1 0 1
1 1 0
9
0 0 0
0 0 2
1 1 1
-1 -1 1
1 -1 1
-1 1 1
1 1 0
1 0 1
0 1 1
 Sample Output
Sample Output
Case #2: 6
 Problem Idea
Problem Idea
解题思路:
【题意】
在三维空间中给出n个点,问你有多少个特殊四面体
特殊四面体定义如下:
1.至少四条边相等;
2.如果恰好只有四条边相等,那么不相等的两条边不相邻
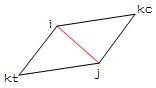
如图
当AB=AC=BD=CD≠(AD,BC),此时,AD与BC异面(不相邻),满足特殊四面体定义第2条
【类型】
计算几何
【分析】
n^4暴力,但实际上复杂度达不到n^4【虽然我觉得还是可以卡掉的,可能是出题人懒得出这种数据了】
暴力枚举两个点,然后再枚举离这两点距离相同的点,如下图
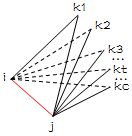
再枚举四个点,判断其构成的四面体是否四条边相等(即![]() ),但是不共面(比如点A,B,C,D,共面可以通过3点(A,B,C)所构成的平面的平面法向量与其中一个向量(A->D)是否垂直来判断)
),但是不共面(比如点A,B,C,D,共面可以通过3点(A,B,C)所构成的平面的平面法向量与其中一个向量(A->D)是否垂直来判断)
再判断这个是不是正四面体,如果是正四边形的话,暴力枚举过程会使得该四面体被重复计算6次(四面体4个顶点任取两个,C(4,2)=6)
否则该四面体被重复计算两次(A与D,B与C两种取法)
【时间复杂度&&优化】
O(n^4)
题目链接→HDU 5839 Special Tetrahedron
 Source Code
Source Code
/*Sherlock and Watson and Adler*/
#pragma comment(linker, "/STACK:1024000000,1024000000")
#include
#include
#include
#include
#include
#include
#include
#include  Problem 1011 Lweb and String
Problem 1011 Lweb and String
Accept: 0 Submit: 0
Time Limit: 2000/1000 MS (Java/Others) Memory Limit : 65536/65536 K (Java/Others)
 Problem Description
Problem Description
Lweb has a string S.
Oneday, he decided to transform this string to a new sequence.
You need help him determine this transformation to get a sequence which has the longest LIS(Strictly Increasing).
You need transform every letter in this string to a new number.
A is the set of letters of S, B is the set of natural numbers.
Every injection f:A→B can be treat as an legal transformation.
For example, a String “aabc”, A={a,b,c}, and you can transform it to “1 1 2 3”, and the LIS of the new sequence is 3.
Now help Lweb, find the longest LIS which you can obtain from S.
LIS: Longest Increasing Subsequence. (https://en.wikipedia.org/wiki/Longest_increasing_subsequence)
 Input
Input
The first line of the input contains the only integer T,(1≤T≤20).
Then T lines follow, the i-th line contains a string S only containing the lowercase letters, the length of S will not exceed 10^5.
 Output
Output
For each test case, output a single line "Case #x: y", where x is the case number, starting from 1. And y is the answer.
 Sample Input
Sample Input
aabcc
acdeaa
 Sample Output
Sample Output
Case #2: 4
 Problem Idea
Problem Idea
解题思路:
【题意】
一个只包含小写字母的字符串S,给每种字母填上相同的数,问得到的数列的最长递增(严格递增)子序列的长度为多少
【类型】
水题
【分析】
因为题目已经规定严格递增
这就使得题目的难度降到了最低
因为相同字母值相同,所以一种字母无论多少个,对LIS的长度贡献只能为1
所以此题就成了求有多少种不同的字母,好吧,暴力扫一遍字符串就可以解决了
【时间复杂度&&优化】
O(n)
题目链接→HDU 5842 Lweb and String
 Source Code
Source Code
/*Sherlock and Watson and Adler*/
#pragma comment(linker, "/STACK:1024000000,1024000000")
#include
#include
#include
#include
#include
#include
#include
#include 
