HDU1874最短路径（dijkstra,Bellman-Ford,Floyd-Warshall算法不同版本合集）

Problem Description

某省自从实行了很多年的畅通工程计划后，终于修建了很多路。不过路多了也不好，每次要从一个城镇到另一个城镇时，都有许多种道路方案可以选择，而某些方案要比另一些方案行走的距离要短很多。这让行人很困扰。

现在，已知起点和终点，请你计算出要从起点到终点，最短需要行走多少距离。

Input

本题目包含多组数据，请处理到文件结束。
每组数据第一行包含两个正整数N和M(0 接下来是M行道路信息。每一行有三个整数A,B,X(0<=A,B 再接下一行有两个整数S,T(0<=S,T

Output

对于每组数据，请在一行里输出最短需要行走的距离。如果不存在从S到T的路线，就输出-1.

Sample Input

3 3

0 1 1

0 2 3

1 2 1

0 2

3 1

0 1 1

1 2

Sample Output

2

-1

题目链接：http://acm.hdu.edu.cn/showproblem.php?pid=1874

先用Bellman-Ford算法做一遍。

简单说一下什么是Bellman-Ford算法，因为图中最长的边只能是V-1的长度（不考虑带负圈的图），从顶点s到顶点t，不会经过同一个顶点2次。那么就进行V-1次循环，每次循环都遍历所有的边，更新边的端点的距离（距顶点s的距离）。

解释一些变量的含义：

edge:存放边的结构体，顶点from到顶点to的权值cost。

G[]:存放边的数组。

注意一点：Bellman-Ford里边数是按照有向边的数目遍历，这题是无向图，所以边数乘以2，得到一个{from,to,cost}的边，额外再加一个{to,from,cost}这样的边。使用邻接表时，无向图都要考虑这点，后面的Dijkstra邻接表版也是要考虑的，无向图的一条边等于2条边。

#include
#include
#include
#include
using namespace std;
#define N 205
#define M 2005
#define inf 0x3f3f3f3f
struct edge{
    int from,to,cost;
}G[M];
int dis[N];
void Bellman_Ford(int start,int n,int m)
{
    int update=0;
    memset(dis,0x3f,sizeof(dis));
    dis[start]=0;
    for(int i=0;idis[G[j].from]+G[j].cost)
            {
                dis[G[j].to]=dis[G[j].from]+G[j].cost;
            }
        }
    }
}
int main()
{
    int n,m,start,end;
    while(~scanf("%d%d",&n,&m)){
        for(int i=0;i<2*m;)
        {
            cin>>G[i].from>>G[i].to>>G[i].cost;
            G[i+1].from=G[i].to;
            G[i+1].to=G[i].from;
            G[i+1].cost=G[i].cost;
            i+=2;
        }
        cin>>start>>end;
        Bellman_Ford(start,n,m);
        printf("%d\n",dis[end]==inf?-1:dis[end]);
    }
    return 0;
}

 

普通版Dijkstra算法（邻接矩阵） 

解释一下变量的含义：

roads[i][j]:邻接矩阵，表示顶点i和顶点j的距离（顶点编号，这题是从0开始）。

dis[i]:起始点start到顶点i的最短距离

vis[i]:标记数组，vis[i]=1,表示顶点i被访问过了，已经算过起始点start到顶点i的最短路了。

 

注意：if(cost

#include
#include
#include//strlen memset头文件
#include//max函数头文件
#include//ceil()函数
using namespace std;
#define N 205
#define inf 0x3f3f3f3f
int roads[N][N],dis[N],vis[N];
void Dijkstra(int n,int start)
{
    int Min,pos;
    memset(vis,0,sizeof(vis));
    for(int i=0;i>from>>to>>cost;
            if(cost>start>>end;
        Dijkstra(n,start);
        printf("%d\n",dis[end]==inf?-1:dis[end]);
    }
    return 0;
}

还有一个模板，这两个模板我都很喜欢，也记录下来：

#include
#include
#include//strlen memset头文件
#include//max函数头文件
#include//ceil()函数
using namespace std;
#define N 205
#define inf 0x3f3f3f3f
int roads[N][N],dis[N],vis[N];
void Dijkstra(int n,int start)
{
    int Min,pos;
    memset(vis,0,sizeof(vis));
    for(int i=0;idis[pos]+roads[pos][j])
            {
                dis[j]=dis[pos]+roads[pos][j];
            }
        }
    }
}
int main()
{
    int n,m,from,to,cost,start,end;
    while(~scanf("%d%d",&n,&m)){
        memset(roads,63,sizeof(roads));
        for(int i=0;i>from>>to>>cost;
            if(cost>start>>end;
        Dijkstra(n,start);
        printf("%d\n",dis[end]==inf?-1:dis[end]);
    }
    return 0;
}

还是dijkstra算法，使用邻接矩阵的复杂度是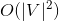不过这次用的是邻接表。使用邻接表的表话，更新最短距离只需要访问每条边即可，因此这部分的复杂度是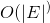。但是每次都要枚举所有的顶点来查找下一个使用的顶点，因此最终复杂度还是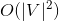，所以需要合适的数据结构来优化。

需要优化的是数值的插入和取出，使用堆可以实现。每个顶点当前的最短距离用堆维护，在更新最短距离时，把对应元素往根的方向移动，这样每次从堆中取出的最小值就是下次要使用的顶点。这样堆中元素共有V，每次取是E次，这样整个算法的复杂度就是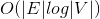，这个还是优化了不少的。

那个continue操作如下如：

先从节点1出发，dis[2]=1,dis[3]=3

然后从节点2出发，dis[3]=2了，下次遍历节点3时，第一次记录的信息没用了，就跳过了（第一次dis[3]=3） 

解释一些变量的含义：

edge:记录边的结构体，有向图中to代表弧头对应的顶点，无向图就是无所谓了，cost就是边的权值了。

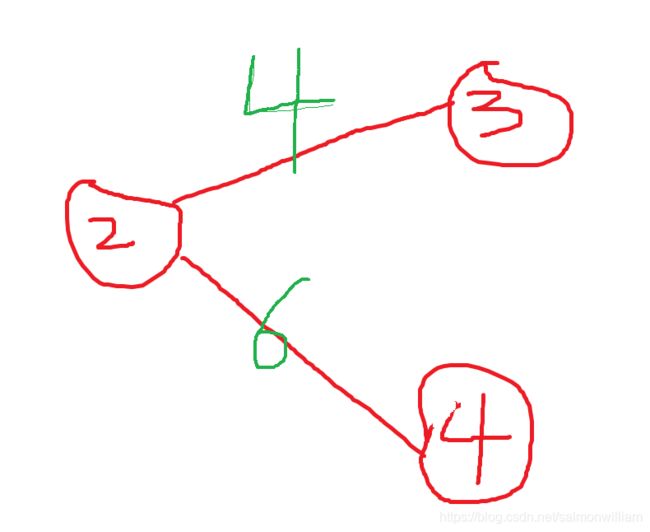
G[N]:是个vector的数组,G的每个元素，比如G[2]对应的就是一个edge类型的vector。画个图吧，比如G[2]=[{3,4},{4,6}],就是这么个意思。

注意：

 edge e={to,cost};
 G[from].push_back(e);
 e={from,cost};
 G[to].push_back(e);

 这个一定要有，因为是无向图，所以是双向的。

#include
#include
#include
#include//strlen memset头文件
#include//max函数头文件
#include//ceil()函数
#include
using namespace std;
#define inf 0x3f3f3f3f
#define N 205
struct edge{
    int to,cost;
};
typedef pair P;
// vector G[N];
int dis[N];
void Dijkstra(vector G[],int n,int start)
{
    priority_queue,greater
 > que;
    for(int i=0;idis[v]+e.cost)
            {
                dis[e.to]=dis[v]+e.cost;
                que.push(P(dis[e.to],e.to));
            }
        }
    }
}

int main()
{
	int n,m,from,to,cost,start,end;
    while(~scanf("%d%d",&n,&m))
    {
        vector G[N];
        for(int i=0;i>from>>to>>cost;
            edge e={to,cost};
            G[from].push_back(e);
            e={from,cost};
            G[to].push_back(e);
        }
        cin>>start>>end;
        Dijkstra(G,n,start);
        printf("%d\n",dis[end]==inf?-1:dis[end]);
    }
	return 0;
}

还有一种算法，虽然复杂度较高O(n3)，但它值得拥有一个名字，在这题是可以AC的。

Floyd_Warshall算法

思路：其实就是个数学的排列组合问题，顶点i到顶点j的最短路经过的节点，无非就是顶点编号从0到n-1这n个节点取不取的问题，所以计算roads[i][j]的最短路时，我就把每个节点都检查一遍，要不要在我的最短路径中出现。

该算法和Bellman-Ford算法一样，可以处理边是负数的情况。而判断图中是否有负圈，只需检查是否存在d[i][i]是负数就可以了。

k的顺序从0-n-1和从n-1到0进行遍历都是可以的。

#include
#include
#include//strlen memset头文件
#include//max函数头文件
#include//ceil()函数
using namespace std;
#define N 205
#define inf 0x3f3f3f3f
int roads[N][N],dis[N],vis[N];

void Floyd_Warshall(int n)
{
    for(int k=0;kroads[i][k]+roads[k][j])
                {
                    roads[i][j]=roads[i][k]+roads[k][j];
                }
            }
        }
    }
}

int main()
{
    int n,m,from,to,cost,start,end;
    while(~scanf("%d%d",&n,&m)){
        memset(roads,63,sizeof(roads));
        for(int i=0;i>from>>to>>cost;
            if(cost>start>>end;
        Floyd_Warshall(n);
        printf("%d\n",roads[start][end]!=inf?roads[start][end]:-1);
    }
    return 0;
}

 

关于Dijkstra为什么不能计算负边，看图

因为前提是:节点v被访问过，即意味着已经找到了从源点到这个点v的最短路径，但若存在负权边，与这个前提矛盾。上图中，d[B]=2,就意味着2就是最短距离，之后不会再更新了，所以结果就不对了。

但是Bellman-Ford算法和Floyd-Warshall算法可以处理负边，而且也可以判断是否存在负圈。