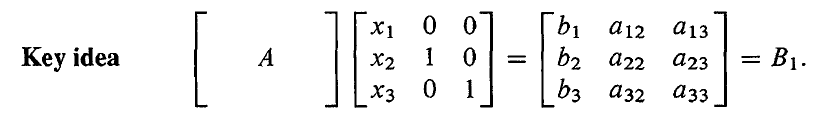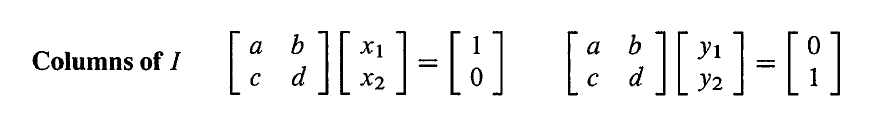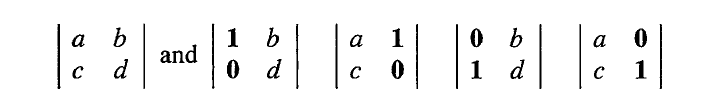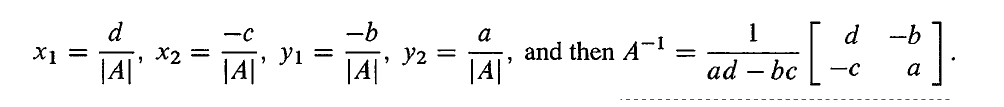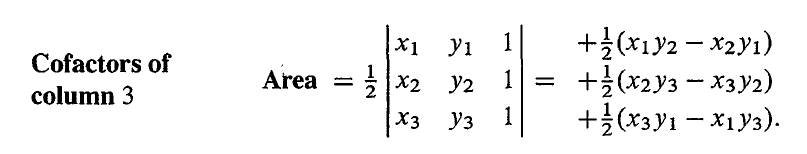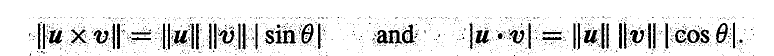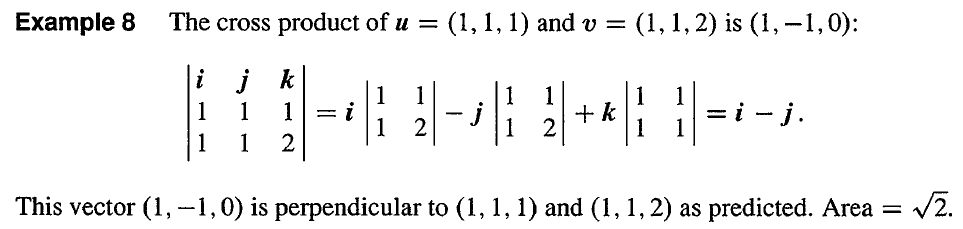线性代数之——克拉默法则、逆矩阵和体积
1. 克拉默法则
这部分我们通过代数方法来求解 A x = b Ax=b Ax=b。
用 x x x 替换单位矩阵的第一列,然后再乘以 A A A,我们得到一个第一列为 b b b 的矩阵,而其余列则是从矩阵 A A A 中对应列直接拷贝过来的。
利用行列式的乘法法则,我们有
∣ A ∣ ( x 1 ) = ∣ B 1 ∣ |A|(x_1)=|B_1| ∣A∣(x1)=∣B1∣
如果我们想要求 x 2 x_2 x2,那么将 x x x 放在单位矩阵的第二列即可。
∣ A ∣ ( x 2 ) = ∣ B 2 ∣ |A|(x_2)=|B_2| ∣A∣(x2)=∣B2∣
同理,如果 d e t A ̸ = 0 det A \not = 0 detA̸=0,我们可以通过行列式来对 A x = b Ax=b Ax=b 进行求解。
x 1 = d e t B 1 d e t A x 2 = d e t B 2 d e t A ⋯ x n = d e t B n d e t A x_1 = \frac{det \space B_1}{det \space A} \quad x_2 = \frac{det \space B_2}{det \space A} \quad \cdots \quad x_n = \frac{det \space B_n}{det \space A} x1=det Adet B1x2=det Adet B2⋯xn=det Adet Bn
其中 B j B_j Bj 就是将矩阵 A A A 的第 j j j 列替换为向量 b b b。
2. 逆矩阵
对于 n = 2 n=2 n=2,我们通过求解 A A − 1 = I AA^{-1}=I AA−1=I 来找到 A − 1 A^{-1} A−1 的每一列。
为了解出 x x x,我们需要五个行列式。
后面的四个行列式分别为 d , − c , − b , a d,-c,-b,a d,−c,−b,a,它们分别是矩阵的代数余子式 C 11 , C 12 , C 21 , C 22 C_{11},C_{12},C_{21},C_{22} C11,C12,C21,C22。
对任意大小的矩阵都满足,当右边是单位矩阵的一列时,克拉默法则中矩阵 B j B_j Bj 的行列式是一个代数余子式。
第一个行列式 ∣ B 1 ∣ |B_1| ∣B1∣ 是代数余子式 C 11 C_{11} C11,第二个行列式 ∣ B 2 ∣ |B_2| ∣B2∣ 是代数余子式 C 12 C_{12} C12,但是它位于逆矩阵的第一列,也就是 (2,1) 的位置。因此有
我们可以进行一个简单的验证,两边同时乘以 A A A。
左边第一行乘以第一列可得
a 11 C 11 + a 12 C 12 + a 13 C 13 = d e t A a_{11}C_{11}+a_{12}C_{12}+a_{13}C_{13} = det \space A a11C11+a12C12+a13C13=det A
第一行乘以第二列可得
a 11 C 21 + a 12 C 22 + a 13 C 23 = 0 a_{11}C_{21}+a_{12}C_{22}+a_{13}C_{23} = 0 a11C21+a12C22+a13C23=0
这可以看作是我们将矩阵 A A A 的第一行复制到第二行得到另外一个矩阵 A ∗ A^* A∗,矩阵 A ∗ A^* A∗ 有两行元素相同,其行列式为零。另外,我们注意到矩阵 A A A 和 A ∗ A^* A∗ 的代数余子式 C 21 , C 22 , C 23 C_{21},C_{22},C_{23} C21,C22,C23 是相同的,因此上式就是矩阵 A ∗ A^* A∗ 的行列式,其值为零。
3. 体积
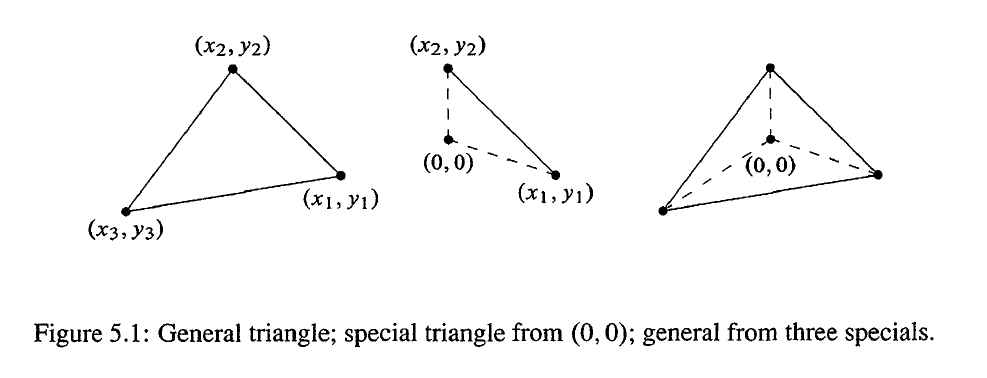
任何人都知道一个长方形的面积——底乘以高,而一个三角形的面积为底乘以高的一半。但是,如果我们只知道三角形三个顶点的坐标为 ( x 1 , y 1 ) , ( x 2 , y 2 ) , ( x 3 , y 3 ) (x_1, y_1),(x_2, y_2),(x_3, y_3) (x1,y1),(x2,y2),(x3,y3),这时候面积为多少呢?
三角形的面积就是 3 × 3 3×3 3×3 行列式的一半,如果其中一个坐标为原点的话,那么行列式就只有 2 × 2 2×2 2×2 了。
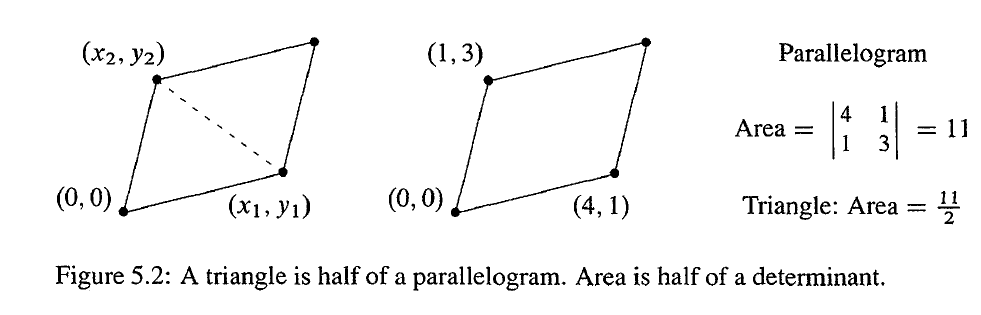
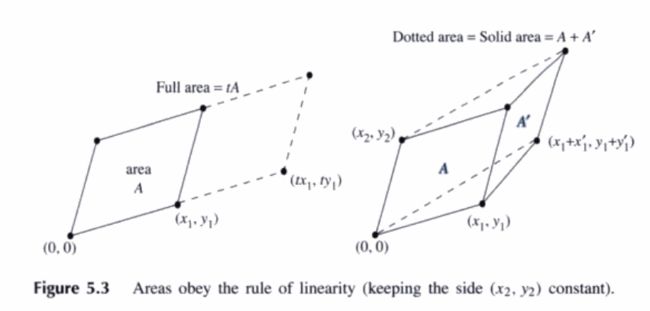
由于平行四边形的面积是三角形面积的两倍,因此从原点开始的平行四边形是一个 2 × 2 2×2 2×2 的行列式。
如果我们能证明平行四边形的面积和行列式具有一样的性质,那么面积就等于行列式。
- 当 A = I A = I A=I 时,平行四边形就变成了单位正方形,面积为 d e t I = 1 det I = 1 detI=1。
- 当两行进行交换的时候,行列式改变符号,但平行四边形还是原来的平行四边形,其面积的绝对值没有改变。
- 当某一行乘以 t t t 后,面积就变为原来的 t t t 倍。当其中一行不变,而另一行加上 ( x 1 ′ , y 1 ′ ) (x_1', y_1') (x1′,y1′) 后,新的平行四边形的面积就为两个平行四边形面积的和。
注意右边的图形是一个平面图形,两个三角形的面积是一样的。我画了一个草图,可能会更直观一点。
S ⋄ O C E B = S ⋄ O A D B + S ⋄ A C E D 因 为 S △ B E D = S △ O C A S_{\diamond OCEB} = S_{\diamond OADB}+S_{\diamond ACED} \quad 因为 \quad S_{\triangle BED}=S_{\triangle OCA} S⋄OCEB=S⋄OADB+S⋄ACED因为S△BED=S△OCA
这个证明虽然不走寻常路,但是它可以很容易扩展到 n n n 维中去,它们都满足行列式的三个基本性质。在三维中,体积等于行列式的绝对值。
4. 叉积
两个向量的叉积定义为:
叉积得到一个新的向量,这个向量垂直于 u u u 和 v v v,而且有 v × u = − u × v v×u = -u×v v×u=−u×v。
-
性质 1: v × u v×u v×u 交换了第二行和第三行,因此有 v × u = − u × v v×u = -u×v v×u=−u×v。
-
性质 2: v × u v×u v×u 垂直于 u u u 和 v v v。
行列式的三行变成了 u u u 、 u u u 和 v v v,因此其值为零。
- 性质 3: 向量和自己的叉积是 0。当 u u u 和 v v v 平行的时候,它们的叉积也为 0。点积涉及余弦,叉积涉及正弦。
**以 u u u 和 v v v 为边的平行四边形的面积等于它们叉积的模,**其实也就是底乘以高。
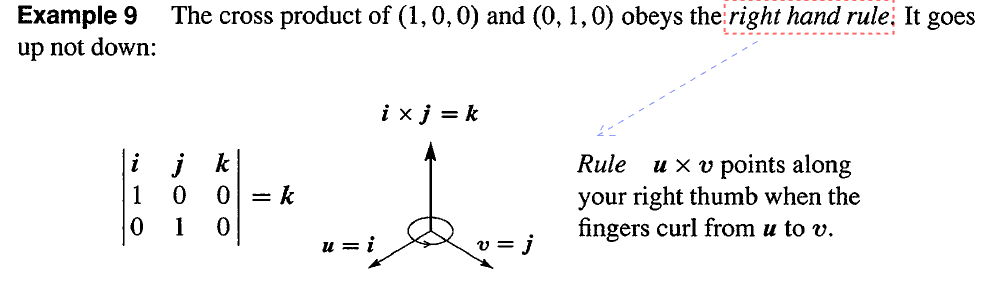
叉积遵守右手定则,叉积后向量的方向为右手大拇指指向的方向。
( u × v ) ⋅ w (u×v)\cdot w (u×v)⋅w 是一个数字,代表边为 u u u 、 v v v 和 w w w 的立方体的体积。
如果这个积为零,说明 u u u 、 v v v 和 w w w 位于一个平面内,体积为零,矩阵是不可逆的,行列式为零。
5. 习题
如果 A A A 是奇异矩阵,那么有
A C T = ( d e t A ) I → A C T = 0 AC^T=(det A)I \to AC^T = 0 ACT=(detA)I→ACT=0
因此, C T C^T CT 的每一列都位于矩阵 A A A 的零空间,我们可以通过求解矩阵的代数余子式来求解 A x = 0 Ax=0 Ax=0。
获取更多精彩,请关注「seniusen」!
![]()