回归分析是一种常见的统计方法,用于确定不同变量间的相互关系。在Excel中可以通过数据分析菜单中的回归功能快速完成。本篇文章将介绍在python中使用机器学习库sklearn建立简单回归模型的过程。
准备工作
首先是开始前的准备工作,在创建回归模型的过程中我们需要使用以下几个库文件,他们分别为sklearn库,numpy库,pandas库和matplotlib库。sklearn库用于计算线性回归模型中的关键参数,并对模型进行检验。numpy和pandas库用于数据导入,创建数据表和一些基础的计算工作。matplotlib库用于绘制散点图。
|
1
2
3
4
5
6
7
8
9
10
|
#导入机器学习linear_model库
from
sklearn
import
linear_model
#导入交叉验证库
from
sklearn
import
cross_validation
#导入数值计算库
import
numpy as np
#导入科学计算库
import
pandas as pd
#导入图表库
import
matplotlib.pyplot as plt
|
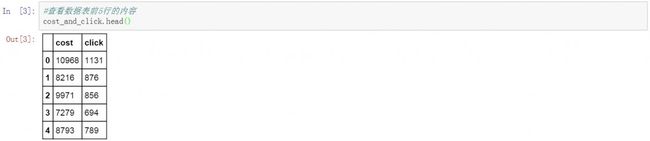
读取并查看数据表
准备工作完成后,开始读取数据,这里我们使用了一组每日广告成本和点击量的数据。将这组数据读取到python中并取名为cost_and_click。通过head函数查看数据表中前5行的内容。以下是数据读取和查看的代码和结果。
|
1
2
|
#读取数据并创建数据表,名称为cost_and_click
cost_and_click
=
pd.DataFrame(pd.read_excel(
'cost_and_click.xlsx'
))
|
|
1
2
|
#查看数据表前5行的内容
cost_and_click.head()
|
设置模型的自变量和因变量
在cost_and_click数据表中,我们将广告成本cost设置为自变量X,将广告点击量click设置为因变量Y。希望通过回归模型发现广告成本对于广告点击量的影响,以及两者间的关系。下面我们将X设置为cost,Y设置为click。并通过shape函数查看了两个变量的行数,共25行,这是我们完整数据表的行数。
|
1
2
3
4
5
6
|
#将广告成本设为自变量X
X
=
np.array(cost_and_click[[
'cost'
]])
#将点击量设为因变量Y
Y
=
np.array(cost_and_click[
'click'
])
#查看自变量和因变量的行数
X.shape,Y.shape
|

绘制散点图
在设置好自变量X和因变量Y后,为了更清楚的看到两者间的关系,我们先使用散点图进行观察,下面是散点图的绘制过程,其中X轴为广告成本数据,Y轴为广告点击量数据。
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
|
#设置图表字体为华文细黑,字号15
plt.rc(
'font'
, family
=
'STXihei'
, size
=
15
)
#绘制散点图,广告成本X,点击量Y,设置颜色,标记点样式和透明度等参数
plt.scatter(X,Y,
60
,color
=
'blue'
,marker
=
'o'
,linewidth
=
3
,alpha
=
0.8
)
#添加x轴标题
plt.xlabel(
'成本'
)
#添加y轴标题
plt.ylabel(
'点击量'
)
#添加图表标题
plt.title(
'广告成本与点击量分析'
)
#设置背景网格线颜色,样式,尺寸和透明度
plt.grid(color
=
'#95a5a6'
,linestyle
=
'--'
, linewidth
=
1
,axis
=
'both'
,alpha
=
0.4
)
#显示图表
plt.show()
|
从散点图中可以看出广告点击量随着广告成本的增加而提升。两者究竟有多强的联系,以及具体的关系如何,我们需要从回归模型中找到答案。
将数据分割为训练集和测试集
原始数据中我们共记录到25天的广告成本和点击量数据。将这25条数据分为两部分,一部分作为训练集创建回归模型,另一部分作为测试集对回归模型的结果进行检验。下面是具体的数据分组代码,使用随机方式从25条记录中抽取40%作为测试集,另外60%作为训练集数据。
|
1
2
|
#将原始数据通过随机方式分割为训练集和测试集,其中测试集占比为40%
X_train, X_test, y_train, y_test
=
cross_validation.train_test_split(X, Y, test_size
=
0.4
, random_state
=
0
)
|
使用shape函数对训练集的数据行数进行查看,共有15行。这15行数据将被用于建立回归模型。
|
1
2
|
#查看训练集数据的行数
X_train.shape,y_train.shape
|

代入线性回归模型
将训练集数据代入到线性回归模型中,以计算关键的参数值。下面是具体的代码和结果。
|
1
2
3
|
#将训练集代入到线性回归模型中
clf
=
linear_model.LinearRegression()
clf.fit (X_train,y_train)
|

计算模型的关键参数
回归模型依据自变量的数量可以分为一元回归模型和多元回归模型,这里我们只有一个自变量X,因此是一元回归模型。其中斜率b1和截距b0是我们要求的关键参数值。
首先计算出回归模型中的斜率值,以下是具体的代码和结果。
|
1
2
|
#线性回归模型的斜率
clf.coef_
|
![]()
其次计算出回归模型的截距,以下是具体的代码和结果。
|
1
2
|
#线性回归模型的截距
clf.intercept_
|
![]()
除此之外,对于回归模型来说还需要计算判定系数,也就是R平方,用以说明自变量对因变量变化的解释度。以下是具体的代码和计算结果。
|
1
2
|
#判定系数R Square
clf.score(X_train,y_train)
|
![]()
有了前面的斜率和截距后,就可以描绘出广告成本与广告点击量之间的关系了,并且可以通过这种关系来对广告点击量的结果进行预测,下面我们在回归模型中将广告成本设置为20000元,经过计算获得预测的广告点击量为1993次。这个预测结果准确吗?我们还需要对回归模型进行评估。
|
1
2
|
#输入自变量预测因变量
clf.predict(
20000
)
|

使用测试集评估模型
评估回归模型的方法就是使用测试集数据,将测试集中的自变量代入到回归模型中,将结果与测试集的因变量进行对比,评估模型的准确性。下面我们将测试集中的自变量代入回归模型,并列出了所有的计算结果。
|
1
2
|
#将测试集的自变量代入到模型预测因变量
list
(clf.predict(X_test))
|
同时我们也列出了测试集中因变量。通过对比可以看到两组数据间的差异,例如第一组数据回归模型的计算结果796,测试集中的因变量736。以及第三组数据908和991。有些数据回归模型的结果大于测试集的数据,而另一些则可能小于测试集的数据。
|
1
2
|
#显示测试集的因变量
list
(y_test)
|
为了衡量回归模型的计算结果与测试集中因变量的数据差异,我们使用误差平方和对两者的差异进行评估。以下是误差平方和的计算公式。为了防止两组数据间差异的正负相互抵消,取平方和。
这里需要说明的是误差平方和指标并不能说明回归模型的结果与测试集数据间的差异大小,它只能用来进行模型间准确率的对比。以下是计算误差平方和的代码和结果。
|
1
2
|
#计算误差平方和
((y_test
-
clf.predict(X_test))
*
*
2
).
sum
()
|



