浴谷 P1020 导弹拦截 解法合集（线性DP、树状数组、二分）

题目描述

某国为了防御敌国的导弹袭击，发展出一种导弹拦截系统。但是这种导弹拦截系统有一个缺陷：虽然它的第一发炮弹能够到达任意的高度，但是以后每一发炮弹都不能高于前一发的高度。某天，雷达捕捉到敌国的导弹来袭。由于该系统还在试用阶段，所以只有一套系统，因此有可能不能拦截所有的导弹。

输入导弹依次飞来的高度（雷达给出的高度数据是≤50000的正整数），计算这套系统最多能拦截多少导弹，如果要拦截所有导弹最少要配备多少套这种导弹拦截系统。

输入输出格式

输入格式：

1行，若干个整数（个数≤100000）

输出格式：

2行，每行一个整数，第一个数字表示这套系统最多能拦截多少导弹，第二个数字表示如果要拦截所有导弹最少要配备多少套这种导弹拦截系统。

 

输入输出样例

输入样例#1：

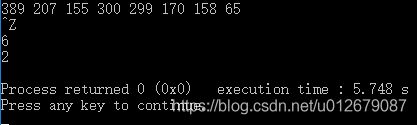
389 207 155 300 299 170 158 65

输出样例#1：

6
2

 

题目分析：

很明显，这题目分两问，第一问就是求一个序列的最长不上升子序列。

第二问求序列的最长上升子序列，就是说一个序列的最长不上升子序列的个数=最长上升序列的长度。

Dilworth定理理论证明省略，简单证明参考这里。

截图如下：

 

思路分析：

求最长子序列长度有一个最常用的方法就是线性动态规划：

  从前往后遍历全部数据，然后找以这个数据结尾的最长子序列的长度。最长上升子序列代码如下

 for(i=1;i<=n;i++)
    {
        f[i]=1;//最少情况为包含自己，长度为1
        for(j=1;j

 

当然有的写法是从后往前找以该数据开头的最长序列，写法如下

for(i=n;i>0;i--)
    {
        f[i]=1;
        for(j=i+1;j<=n;j++)
            if(a[j]<=a[i])
                f[i]=max(f[j]+1,f[i]);
        ans=max(ans,f[i]);
    }

其实都一个意思，如下

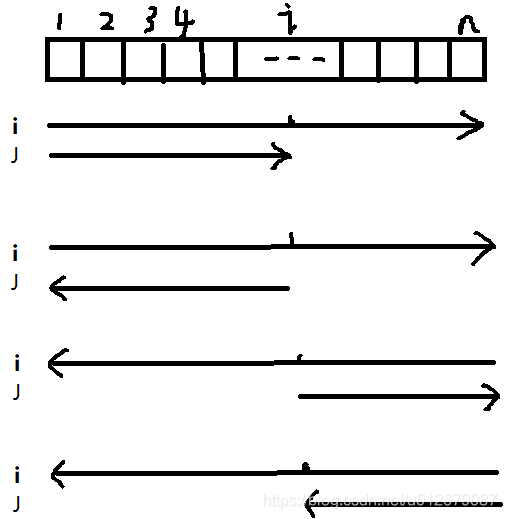
可以这么理解：无是从前开始找以该位置结束的子序列，还是从后开始找该位置开头的子序列，DP数组都是从端点开始。

代码如下：

#include
using namespace std;
#define MAXX 100010
int a[MAXX],f[MAXX];
int main()
{
    int i=0,j;
    int ans=0;
    while(scanf("%d",&a[++i])!=EOF);
    int n=i-1;
    for(i=n;i>0;i--)
    {
        f[i]=1;
        for(j=i+1;j<=n;j++)
            if(a[j]<=a[i])
                f[i]=max(f[j]+1,f[i]);
        ans=max(ans,f[i]);
    }
    cout<

测试数据时遇到点小问题就是无限输入，解决如下： ctrl + z ，然后回车

 

很明显，以上算法的时间复杂度是O(n^2)，而数据的个数有10^5个，肯定会超时，需要把时间降到nlogn。

 

二分查找优化：

加入一个数组，用来存储最长子序列，该数组的长度也就是最后的答案了。

在存储最长子序列的过程中，当遇到比该数组（序列）最后一个数大的时候，需要更新数组（序列），在该数组中找出刚好比这个数大的那个数的后一个位置，然后替换。

那么二分的思想在哪里呢？就是这个查找过程。

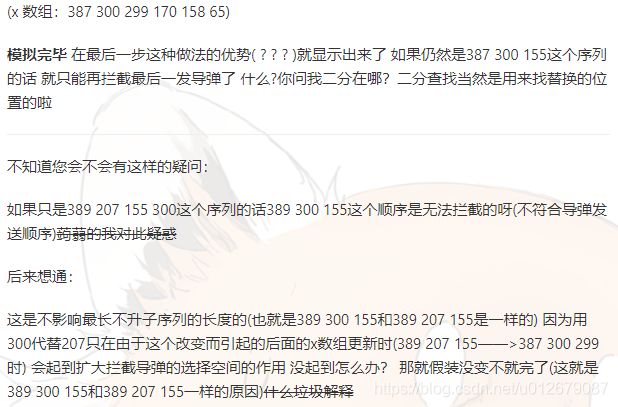
具体过程的模拟参考这里

截图如下：

代码：

#include
using namespace std;
#define MAXX 100010
int a[MAXX];
int f[MAXX];  //存最长子序列
int main()
{
    int i=0;
    int len=0;
    while(scanf("%d",&a[++i])!=EOF);
    int n=i-1;
    f[++len]=a[1];
    for(i=2;i<=n;i++)
    {
        if(a[i]<=f[len]) f[++len]=a[i];
        else//更新f，二分查找找出该更新的位置
        {
            int l=1,r=len;
            while(l>1;
                if(f[mid]>=a[i]) l=mid+1;//我就记住了这么一种，左右区间都能取到，用l=mid+1
                else r = mid;
            }
            f[l]=a[i];
        }
    }
    cout<f[len]) f[++len]=a[i];
        else//更新f，二分查找找出该更新的位置
        {
            int l=1,r=len;
            while(l>1;
                if(f[mid]>=a[i]) r=mid;
                else l = mid+1;
            }
            f[l]=a[i];
        }
    }
    cout<

---

以下才是好玩的！！！

 

树状数组优化：

回想一下，我们用O(n^2)朴素算法实现的时候为什么超时了？？不就是第二重循环还需要遍历数组，那能不能不遍历或者加快遍历速度呢？  树状数组：当我不存在呀！

树状数组最基本的用法是用来维护一个数组前n项的和，也就是说需要查一个数组的前m项和的时候，可以快速查找得到。

该题可以说很适用了，我用一个树状数组维护前m个数的最长子序列数，查找就很快了。

当然还有一个东西叫线段数，树状数组能干的他基本都能干，还干得更好，就是代码长了点。

树状数组入门参考这里

 

代码如下：

#include
using namespace std;
#define MAXX 100010
int a[MAXX];
int f[MAXX];  //树状数组

int lowbit(int x)
{
    return -x&x;
}

void update(int x,int c)
{
    for(int i=x;i<=MAXX;i+=lowbit(i)) f[i]=max(f[i],c);
}

int query(int x)
{
    int ret=0;
    //for(int i=1;i<=x;i+=lowbit(i)) ret=max(ret,f[i]);//这行是不行的，会查漏
    for(int i=x;i>=1;i-=lowbit(i)) ret=max(ret,f[i]);

    //for(int i=x;i=1;i--)//以i开头的最长子序列
    {
        int q=query(a[i])+1;
        update(a[i],q);
        ans = max(q,ans);
    }
    cout<

用树状数组得时候注意一点，就是循环的时候以该数开头还是结尾会有点区别，可以在树状数查询的时候分向前向后两种查询方式，也可以以i开头还是结尾的时候分开。（该代码为后者，查询时统一向前查询）

还不理解的可以手动模拟一下测试数据的运行过程。

然后这个题也没啥好说的了，有人直接用STL函数：lower_bound(),和upper_bound()，原谅我对STL不熟。

 

写博客好耗时间，不能再细写了。就这么多吧