Leetcode 105 & 106. Construct Binary Tree from Preorder and Inorder & Inorder and Postorder

Construct Binary Tree from Preorder and Inorder

Given preorder and inorder traversal of a tree, construct the binary tree.

Note:
You may assume that duplicates do not exist in the tree.

For example, given

preorder = [3,9,20,15,7]
inorder = [9,3,15,20,7]
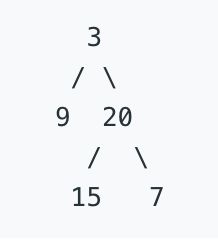
Return the following binary tree:

hash
Use a dictionary to store the number in inorder and its index. Find position of the root in inorder in O(1).
slow version

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, x):
#         self.val = x
#         self.left = None
#         self.right = None

class Solution:
    def buildTree(self, preorder, inorder):
        """
        :type preorder: List[int]
        :type inorder: List[int]
        :rtype: TreeNode
        """
        
        def builder(start,end):
            if end-start<0:
                return None 
            tmp=preorder.pop(0)
            index=0
            for i in range(start,end+1):#slow part
                if inorder[i]==tmp:
                    index=i
            root=TreeNode(tmp)
            root.left=builder(start,index-1)
            root.right=builder(index+1,end)
            return root
        return builder(0,len(inorder)-1)

fast version

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, x):
#         self.val = x
#         self.left = None
#         self.right = None

class Solution:
    def buildTree(self, preorder, inorder):
        """
        :type preorder: List[int]
        :type inorder: List[int]
        :rtype: TreeNode
        """
        
        def builder(start,end):
            if end-start<0:
                return None 
            tmp=preorder.pop(0)
            index=inorderdict[tmp]
            root=TreeNode(tmp)
            root.left=builder(start,index-1)
            root.right=builder(index+1,end)
            return root
        inorderdict={}
        for i in range(len(inorder)):
            inorderdict[inorder[i]]=i
        return builder(0,len(inorder)-1)

Construct Binary Tree from Inorder and Postorder

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, x):
#         self.val = x
#         self.left = None
#         self.right = None

class Solution:
    def buildTree(self, inorder, postorder):
        """
        :type inorder: List[int]
        :type postorder: List[int]
        :rtype: TreeNode
        """
        def builder(istart,iend,pstart,pend):
            if iend-istart<0 or pend-pstart<0:
                return None
            tmp=postorder[pend]
            iindex=inorderdict[tmp]
            root=TreeNode(tmp)
            root.left=builder(istart,iindex-1,pstart,pstart+iindex-1-istart)
            root.right=builder(iindex+1,iend,pstart+iindex-istart,pstart-istart+iend-1)
            return root
        inorderdict={}
        for i in range(len(inorder)):
            inorderdict[inorder[i]]=i
        return builder(0,len(inorder)-1,0,len(postorder)-1)