336. 回文对
ID: 336
TITLE: 回文对
TAG: Java,Python
方法一:暴力法
暴力法去解决这个问题是个很好的开始。对于这个问题是非常简单的。我们遍历所有可能的字符串组合结果并检查它们是否是回文
算法:
我们可以使用嵌套循环来实现这一点,每个循环遍历数组中的每个索引。我们检查每一对是否形成回文。这个步骤有很多方法。在这里我推荐最简单的方法:判断组合成的字符串正向和反转后的字符串是否相等。
需要注意的一个重要的边界情况是 i = j。i 和 j 必须是不一样的。识别这个边界情况是很重要的,因为我们在优化算法时也需要小心。
def palindromePairs(self, words: List[str]) -> List[List[int]]:
pairs = []
for i, word_1 in enumerate(words):
for j, word_2 in enumerate(words):
if i == j:
continue
combined_word = word_1 + word_2
if combined_word == combined_word[::-1]:
pairs.append([i, j])
return pairs
class Solution {
public List<List<Integer>> palindromePairs(String[] words) {
List<List<Integer>> pairs = new ArrayList<>();
for (int i = 0; i < words.length; i++) {
for (int j = 0; j < words.length; j++) {
if (i == j) continue;
String combined = words[i].concat(words[j]);
String reversed = new StringBuilder(combined).reverse().toString();
if (combined.equals(reversed)) {
pairs.add(Arrays.asList(i, j));
}
}
}
return pairs;
}
}
复杂度分析
n n n 指的是单词的数量, k k k 指的是最长单词的长度。
- 时间复杂度: O ( n 2 ⋅ k ) O(n^2 \cdot k) O(n2⋅k)。总共有 n 2 n^2 n2 个单词对。然后组合单词,反转,判断是否相等需要 2 k 2k 2k 的时间。所以总共的时间复杂度是 O ( n 2 ⋅ k ) O(n^2 \cdot k) O(n2⋅k)。
- 辅助空间复杂度: O ( n 2 + k ) O(n^2 + k) O(n2+k),辅助空间我们不考虑输入的大小。
- 我们从输出的大小开始考虑。在最坏的情况下,会有 n ⋅ ( n − 1 ) n \cdot (n - 1) n⋅(n−1) 对整数在输出列表。因为 n n n 个单词都可以与其他任何 n − 1 n-1 n−1 个单词配对。每对将向输入列表中添加 2 个整数,总计 2 ⋅ n ⋅ ( n − 1 ) = 2 ⋅ n 2 − 2 ⋅ n 2 \cdot n \cdot (n - 1) = 2 \cdot n ^ 2 - 2 \cdot n 2⋅n⋅(n−1)=2⋅n2−2⋅n。去掉常量和不重要的项,我们的输出大小为 O ( n 2 ) O(n^2) O(n2)。
- 现在来考虑我们使用多少口评鉴来找到所有的组合对?每一次循环,我们组合两个单词和创建一个组合单词的逆向副本。需要 4 ⋅ k 4 \cdot k 4⋅k,也就是 O ( k ) O(k) O(k)。这里不需要乘以 n 2 n^2 n2,因为我们并没有对该临时变量进行保留。
- 总共为 O ( n 2 + k ) O(n^2 + k) O(n2+k),这似乎 k k k 可以省略掉。并非如此,因为如果单词很长,但是单词列表很短,那么 k k k 很可能比 n 2 n^2 n2 要大。
- 也可以将其优化为 O ( n 2 ) O(n^2) O(n2)。通过使用原地算法来确定两个给定单词是否构成回文,将 k k k 变成 1 1 1。因此能够省略。
- 空间复杂度: O ( n ⋅ k + n 2 ) O(n \cdot k + n ^ 2) O(n⋅k+n2)。这里我们考虑输入的大小,有 n n n 个单词,最大的长度为 k k k。这需要 O ( n ⋅ k ) O(n \cdot k) O(n⋅k) 的大小。像上面一样,我们不能够确定 $k > n $ 或 k < n k < n k<n。因此,我们不知道 O ( n 2 + k ) O(n ^ 2 + k) O(n2+k) 和 O ( n ⋅ k ) O(n \cdot k) O(n⋅k) 哪一个更大。
方法二:散列
每一对都进行检查开销太大,有没有一种方法能够避免检查绝对不会形成回文的情况呢?为了回答这个问题,我们需要探索形成回文的特性。
如果你不习惯用这种类型的探索和推理可能会有点挑战性,所以我们会用一些例子来解决它,然后将尝试证明我们的发现。之后,再研究如何在代码中高效的实现它。
我们有什么方法用两个词组成回文?
最简单的方法就是取两个彼此相反的单词组合在一起。在这种情况下,我们得到两个回文,因为可以调换顺序。
我们知道,总是两个单词能够形成彼此相反的回文,且单词是不同的。问题陈述中很清楚,单词列表中没有重复的单词。
现在让我们思考所有可以与单词 1 "CAT" 单词配对形成回文的单词。我们假设单词 2 的所有可能性都是 8 个字母长。虽然这个假设过于具体,但是记住我们知识将其最为识别可能案例的起点。我们稍后会做一个更全面的证明。

根据回文的逻辑,我们知道倒数第二和第三个字母必须是 "A" 和 "T"。

接下来我们使用数字强调字母必须相同,因为要满足回文的特性。


最后一个字母可以是任何情况。

我们的是实验表明如果单词 2 是一个长度为 5 的回文连接着单词 1 的逆转单词。则组合单词 1 和单词 2 可以形成一个回文。

另一个情况是,如果单词 1 是单词 2 的逆转单词连接 长度为 5 的回文,则合并单词 1 和单词 2 也将是一个回文。

别忘了,空字符串也是一个有效的词。这是一个重要的边界情况,我们想想如何形成一个回文呢?
空字符串只会与非空字符串组合。如果这个非空字符串是一个回文,则我们将得到一个有效的回文。反之则不会。所有任何单词本身是回文则会与空字符串组合形成回文。
根据你的实现,可能不需要将情况视作特殊情况,因为它实际上是情况 2 和情况 3 的子情况。只是反转的长度为-0。不过一定要在此情况测试你的实现。
我们怎么样才能证明我们已经确定了所有的情况?
通过实验,我们发现了一些情况。对于这类问题让自己相信我们已经考虑了所有情况是非常重要的。一个方法是考虑每对单词的相对长度。每对单词中的相对长度有两种情况。
- 两个单词是同样的长度。
- 两个单词是不同的长度。
然后我们需要展示这两种情况如何完全映射到我们已经发现的回文对情况。我们将通过考虑组合词(在第一个词后面附加第二个词)的中间位置来实现这一点。
第一个可能性是组合词的中心是这两个词之间。

若形成回文对,则字母应该在中间形成中心对称,下图用数字说明两个字母必须相同。
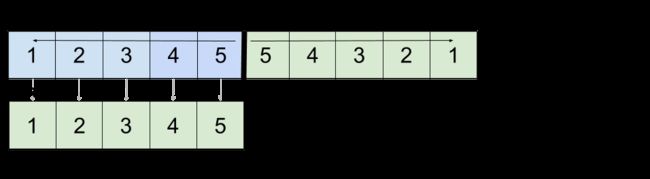
因此,当长度相同的两个词形成回文,那一定是单词 1 与单词 2 彼此相反。这相当于情况 1。
第二个可能性是一个词短于另一个词。我们先假设单词 1 是较短的。
像之前一个样,因为单词 1 较短,则组合词的中心将在单词 2 中。

我们知道回文必须在中心点形成中心对称,因此在单词 2 的末尾必须是单词 1 的相反单词。

现在剩下单词 1 和末尾单词 1 相反词之间的中间区域。由于要使得整个组合词是回文,则中间的区域也必须是个回文。
使用同样的思路,很容易就可以表明,当单词 2 是较短的情况下,相当于情况 3。
因此,我们已经证明了在探索过程中发现的 3 个回文情况涵盖了两个单词形成回文对的情况。
我们如何将该思路写进代码里?
把这些思路放进代码中最简单的方法是遍历单词列表并对每个单词执行以下操作。
如果这初步的解释令人困惑,不用紧张。有进一步的例子在下面进行解释。
- 检查单词中是否存在相反的词,如果有,这对应于情况 1。
- 检查每个单词的后缀是否为回文。如果是回文,则反转剩余的前缀并检查它是否在列表中。如果是,则这对应于情况 2。
- 检查每个单词的前缀是否为回文。如果是回文,则反转剩余的后缀并检查是否在列表中。如果是,则这对应于情况 3。
例如,我们有单词 "banana"。首先检查 "ananab" 是否存在在列表中。
然后确认 "banana" 的所有回文后缀。对于每一个情况,我们取剩余的前缀反转并检查列表中是否有该词。
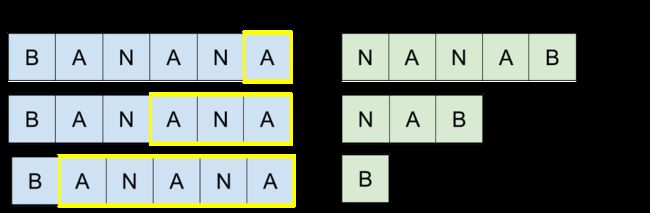
对 "banana" 所有的回文前缀做相同的操作,这里只有一种情况。

这里最具挑战的想法是,我们将当前单词视为情况 2 中的单词 2。我们这样做的原因是,若将其视为单词 1 意味着我们必须猜测单词 2 的所有可能前缀,这将非常低效。
为了保证实现的有效性,我们将所有的单词放到以单词为键,原始索引为值的哈希表中(因为输出必须是单词的原始索引)。
算法:
如果一个单词的前缀形成一个回文,则将其后缀称为有效后缀。函数 allvalidsuffix 查找所有这样的后缀。例如单词 "exempt" 的有效后缀是 "xempt"(移除 "e") 和 "mpt"(移除 "exe")。
如果一个单词的后缀形成一个回文,则将其前缀称为有效前缀。函数 allValidPrefixes 以与 allvalidsuffix 类似的方式查找所有这样的前缀。在这里,可以将函数的很多代码组合在一起,但是在反复讨论这个问题后,决定不使用这种做法,因为虽然减少了代码的长度和重复。但是理解它的认知负荷更高。在你自己的单吗中,合并它是可以的。
情况 1 的例子是通过反转当前词并查找。需要注意的一个边界情况是,如果单词本身就是一个回文,那么我们并不想添加包含同一个单词的对。这种情况只出现在情况 1,因为情况 1 就是处理单词长度相同的情况。
通过调用 allvalidsuffix,然后反转找到的每个后缀并在哈希表中查找它们。
通过调用 allValidPrefixes,然后反转找到的每个前缀并在哈希表中查找它们。
通过认识到情况 1 实际上只是情况 2 和情况 3 的一个特例,可以进一步简化(这里不做)。这是因为空字符串是任何单词的回文前缀和后缀。
def palindromePairs(self, words):
def all_valid_prefixes(word):
valid_prefixes = []
for i in range(len(word)):
if word[i:] == word[i:][::-1]:
valid_prefixes.append(word[:i])
return valid_prefixes
def all_valid_suffixes(word):
valid_suffixes = []
for i in range(len(word)):
if word[:i+1] == word[:i+1][::-1]:
valid_suffixes.append(word[i + 1:])
return valid_suffixes
word_lookup = {word: i for i, word in enumerate(words)}
solutions = []
for word_index, word in enumerate(words):
reversed_word = word[::-1]
# Build solutions of case #1. This word will be word 1.
if reversed_word in word_lookup and word_index != word_lookup[reversed_word]:
solutions.append([word_index, word_lookup[reversed_word]])
# Build solutions of case #2. This word will be word 2.
for suffix in all_valid_suffixes(word):
reversed_suffix = suffix[::-1]
if reversed_suffix in word_lookup:
solutions.append([word_lookup[reversed_suffix], word_index])
# Build solutions of case #3. This word will be word 1.
for prefix in all_valid_prefixes(word):
reversed_prefix = prefix[::-1]
if reversed_prefix in word_lookup:
solutions.append([word_index, word_lookup[reversed_prefix]])
return solutions
class Solution {
private List<String> allValidPrefixes(String word) {
List<String> validPrefixes = new ArrayList<>();
for (int i = 0; i < word.length(); i++) {
if (isPalindromeBetween(word, i, word.length() - 1)) {
validPrefixes.add(word.substring(0, i));
}
}
return validPrefixes;
}
private List<String> allValidSuffixes(String word) {
List<String> validSuffixes = new ArrayList<>();
for (int i = 0; i < word.length(); i++) {
if (isPalindromeBetween(word, 0, i)) {
validSuffixes.add(word.substring(i + 1, word.length()));
}
}
return validSuffixes;
}
// Is the prefix ending at i a palindrome?
private boolean isPalindromeBetween(String word, int front, int back) {
while (front < back) {
if (word.charAt(front) != word.charAt(back)) return false;
front++;
back--;
}
return true;
}
public List<List<Integer>> palindromePairs(String[] words) {
// Build a word -> original index mapping for efficient lookup.
Map<String, Integer> wordSet = new HashMap<>();
for (int i = 0; i < words.length; i++) {
wordSet.put(words[i], i);
}
// Make a list to put all the palindrome pairs we find in.
List<List<Integer>> solution = new ArrayList<>();
for (String word : wordSet.keySet()) {
int currentWordIndex = wordSet.get(word);
String reversedWord = new StringBuilder(word).reverse().toString();
// Build solutions of case #1. This word will be word 1.
if (wordSet.containsKey(reversedWord)
&& wordSet.get(reversedWord) != currentWordIndex) {
solution.add(Arrays.asList(currentWordIndex, wordSet.get(reversedWord)));
}
// Build solutions of case #2. This word will be word 2.
for (String suffix : allValidSuffixes(word)) {
String reversedSuffix = new StringBuilder(suffix).reverse().toString();
if (wordSet.containsKey(reversedSuffix)) {
solution.add(Arrays.asList(wordSet.get(reversedSuffix), currentWordIndex));
}
}
// Build solutions of case #3. This word will be word 1.
for (String prefix : allValidPrefixes(word)) {
String reversedPrefix = new StringBuilder(prefix).reverse().toString();
if (wordSet.containsKey(reversedPrefix)) {
solution.add(Arrays.asList(currentWordIndex, wordSet.get(reversedPrefix)));
}
}
}
return solution;
}
}
复杂度分析
n n n 指的是单词的数量, k k k 指的是最长单词的长度。
- 时间复杂度: O ( k 2 ⋅ n ) O(k^2 \cdot n) O(k2⋅n)。
- 建立哈希表需要 O ( n ⋅ k ) O(n \cdot k) O(n⋅k) 的时间。每个单词需要 O ( k ) O(k) O(k) 的时间插入并且有 n n n 个单词。
- 然后,对于 n n n 个单词,每个单词我们将搜索三个不同的情况。首先是这个词本身的相反词。这需要 O ( k ) O(k) O(k) 的时间。第二个情况是回文跟另一个词的相反词。第三种情况的另一个词的相反词后跟回文。这两个情况的花费是一样的,所以我们就看前面的情况。我们需要找到给定单词的所有回文前缀。查找单词的所有回文前缀可以在 O ( k 2 ) O(k^2) O(k2) 的时间内完成。因为有 k k k 个可能的前缀,检查每个前缀需要 O ( k ) O(k) O(k) 的时间,所以对于每个单词,我们都要进行 k 2 + k 2 + k k^2 + k^2 + k k2+k2+k 处理,由于有 n n n 个单词,所以结果是 O ( k 2 ⋅ n ) O(k^2 \cdot n) O(k2⋅n)。
- 值得注意的是,前面的方法成本为 O ( n 2 ⋅ k ) O(n^2 \cdot k) O(n2⋅k),因此,这种方法并不是在任何情况下更好。只有当 n > k n > k n>k 的情况下更好,在测试用例中测试解决方案中也确实如此。
- 空间复杂度: O ( ( k + n ) 2 ) O((k + n)^2) O((k+n)2)。
- 像以前一样,我们有几个部分需要考虑,然而这一次,无论我们是否在计算中包含输入,空间复杂度都是相同的。因为该算法会创建一个与输入大小相同的哈希表。
- 在输入中,有 n n n 个单词,每个单词最长的长度为 k k k。这里就需要 O ( n ⋅ k ) O(n \cdot k) O(n⋅k)。然后,我们将使用 n n n 个大小为 k k k 的键去构造一个哈希表。哈希表的大小与原始输入相同,因此也是 O ( n ⋅ k ) O(n \cdot k) O(n⋅k)。
- 对于每个单词,我们将列出需要在哈希表中查找的所有可能成对的单词。在最坏的情况下,将有 k k k 个单词查找,长度最大为 k k k。这意味着每一次循环,我我们最多使用 k 2 k^2 k2 的空间作为查找列表。这可以通过一次只创建一个单词来优化到 O ( k ) O(k) O(k)。不过,在实际操作中,由于字符串的处理方式,这不太可能产生太大的影响。所以,我们会说我们使用了额外的 O ( k 2 ) O(k^2) O(k2) 内存。
- 确定输出的大小与其他方法相同。在最坏的情况下,输出列表中将有 n ⋅ ( n − 1 ) n \cdot (n - 1) n⋅(n−1) 对整数,因为每个单词都可以与任何其他 n − 1 n-1 n−1 个单词配对。每对将向输出列表中添加两个整数,总计 2 ⋅ n ⋅ ( n − 1 ) = 2 ⋅ n 2 − 2 ⋅ n 2 \cdot n \cdot (n - 1) = 2 \cdot n ^ 2 - 2 \cdot n 2⋅n⋅(n−1)=2⋅n2−2⋅n。去掉常量和不重要的项,我们的输出列表大小为 O ( n 2 ) O(n^2) O(n2)。
- 把这些结合到一起,我们得到 2 ⋅ n ⋅ k + k 2 + n 2 = ( k + n ) 2 2 \cdot n \cdot k + k ^ 2 + n ^ 2 = (k + n)^2 2⋅n⋅k+k2+n2=(k+n)2, which is O ( ( k + n ) 2 ) O((k + n)^2) O((k+n)2)。



