二分图的匈牙利算法（用于解决最大匹配问题）

二分图：如果图中点可以被分为两组，并且使得所有边都跨越组的边界，则就是一个二分图（不含有【含有奇数条边的环】的图）
匹配：在图论中，一个匹配是一个边的集合，其中任意两条边都没有公共顶点。
{最大匹配：所含匹配边数最多的匹配 完美匹配：所有的顶点都是匹配点}
增广路：从一个未匹配点出发，走交替路，如果途径另一个未匹配点（出发的点不算），则这条交替路称为增广路（agumenting path）。例如，图 5 中的一条增广路如图 6 所示（图中的匹配点均用红色标出）：


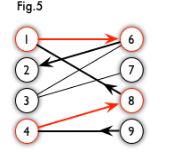
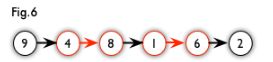
匈牙利算法
（复杂度很高n^3）：基本思想：通过寻找增广路，把增广路中的匹配边和非匹配边的身份交换，这样就会多出一条匹配边，直到找不到增广路为止。
以杭电2063 过山车举个栗子
AC代码如下

#include 
using namespace std;

const int maxn = 510;
int line[maxn][maxn];//建立一个邻接矩阵
int used[maxn];//这个女生有没有被匹配到
int nxt[maxn];//如果女生匹配到了那么男生是谁
int k,n,m,u,v;
//匈牙利算法的核心语句
bool findd(int x)
{
    for(int i = 1;i <= m;i++)
    {
        if(line[x][i] != 0 && used[i] == 0)//前面条件是证明这个男生和这个女生是互相喜欢的+后面这个女生名花无主
        {
            used[i] = 1;
            if(nxt[i] == 0 || (findd(nxt[i]) != 0))//如果这个妹子没有匹配到人或者可以找到另外一个喜欢的男生
            {
                nxt[i] = x;
                //为当前男生寻找到妹子
                return true;
            }
        }
    }
    return false;
}
int match()
{
    int sum = 0;
    for(int i = 1;i <= n;i++)
    {
        memset(used,0,sizeof(used));//每一轮都要对used清空
        if(findd(i)) sum++;
    }
    return sum;
}

int main()
{
    int u,v;
    ios::sync_with_stdio(false);//用来关闭cin和cout与cstdio的同步，能加快cin和cout的输入，在极端情况下接近scanf和printf，大部分情况下还是没有scanf和printf效率高
    while(cin>>k && k)
    {
        cin>>n>>m;
        memset(nxt,0,sizeof(nxt));
        memset(line,0,sizeof(line));
        while(k--)
        {
            cin>>u>>v;
            line[u][v] = 1;
        }
        cout<

上面这道题就是大概理解一下匈牙利的过程，下面再补一道题题解。
杭电 2236 无题二
emmm，刚上来第一眼觉得是搜索，hhh，见到的题太少了，题应该是二分图，矩阵，左边行右边列，寻找完美匹配。（我觉得比较难）

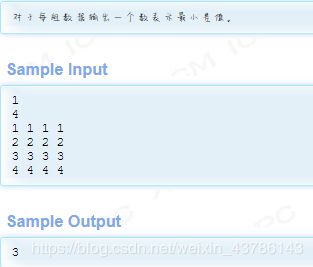
思路：行列只能一个，想到二分图，然后二分区间长度，枚举下限，就能求出哪些边是能用的，然后建图跑二分图，如果最大匹配等于n就是符合的
跑一遍代码，基本就明白了（自我嫌弃.jpg）

#include
using namespace std;
#define mms(x) memset(x, 0, sizeof x)
const int MAX = 105;
int nex[MAX], line[MAX][MAX];
int n, maxn, minn, ans, mid, p;
bool used[MAX];
bool dfs(int x)
{
    for(int i = 1; i <= n; i++)
        if(!used[i] && line[x][i] >= p && line[x][i] <= p + mid)
        {
            used[i] = 1;
            if(!nex[i] || dfs(nex[i]))
            {
                nex[i] = x;
                return true;
            }
        }
    return false;
}
bool match()
{
    mms(nex);
    for(int i = 1; i <= n; i++)
    {
        mms(used);
        if(!dfs(i))
            return false;
    }
    return true;
}
void Bsearch()
{
    int r = maxn - minn, l = 0, flag;
    while(l <= r)
    {
        flag = 0;
        mid = (l + r) >> 1;
        for(p = minn; p + mid <= maxn; p++)
            if(match())
            {
                flag = 1;
                break;
            }
        if(flag)
        {
            ans = mid;
            r = mid - 1;
        }
        else
            l = mid + 1;
    }
}
int main()
{
    int N;
    cin >> N;
    while(N--)
    {
        minn = MAX;
        maxn = -MAX;
        cin >> n;
        for(int i = 1; i <= n; i++)
            for(int j = 1; j <= n; j++)
            {
                cin >> line[i][j];
                maxn = max(maxn, line[i][j]);
                minn = min(minn, line[i][j]);
            }
        ans = MAX;
        Bsearch();
        cout << ans << endl;
    }
    return 0;
}

emmm，这篇文章是为了kuangbin B - Prime Independence 二写的，没想到……卡匈牙利算法……嘤嘤嘤……
只能先偷来别人的ac代码，还没弄懂……我自闭了……

#include
#define ll long long
using namespace std;
const int maxn = 50000;
 
int t, n, n1, n2;
 
vector g[maxn + 10];
int mx[maxn +10], my[maxn + 10];
queue que;
int dx[maxn + 10], dy[maxn + 10], num[maxn + 10], id[10*maxn + 10], pos[10*maxn + 10];
bool vis[maxn + 10];
 
 
 
bool Find(int u) {
    for(int i = 0; i < g[u].size(); i++){
        if(!vis[g[u][i]] && dy[g[u][i]] == dx[u] + 1){
            vis[g[u][i]] = true;
            if(!my[g[u][i]] || Find(my[g[u][i]])) {
                mx[u] = g[u][i];
                my[g[u][i]] = u;
                return true;
            }
        }
    }
    return false;
}
 
int Hmatch()
{
    memset(mx, 0, sizeof(mx));
    memset(my, 0, sizeof(my));
    int ans = 0;
    while(true) {
        bool flag = false;
        while(!que.empty()) que.pop();
        memset(dx, 0, sizeof(dx));
        memset(dy, 0, sizeof(dy));
        for(int i = 1; i <= n1; i++)
            if(!mx[i]) que.push(i);
        while(!que.empty()) {
            int u = que.front();
            que.pop();
            for(int i = 0; i < g[u].size(); i++)
                if(!dy[g[u][i]]) {
                    dy[g[u][i]] = dx[u] + 1;
                    if(my[g[u][i]]) {
                        dx[my[g[u][i]]] = dy[g[u][i]] + 1;
                        que.push(my[g[u][i]]);
                    } else flag = true;
                }
        }
        if(!flag) break;
        memset(vis, 0, sizeof(vis));
        for(int i = 1; i <= n1; i++)
         if(!mx[i]&&Find(i)) ans++;
    }
    return ans;
}
 
void init()
{
    n1 = 0, n2 = 0;
    cin>>n;
    memset(num, 0, sizeof(num));
    memset(id, 0, sizeof(id));
    memset(pos, 0, sizeof(pos));
    for(int i  = 1; i <= n; i++) scanf("%d", &num[i]);
    sort(num+1, num+n+1);
    for(int i  = 1; i <= n; i++) pos[num[i]] = i;
}
 
 
int main()
{
    int cas = 0;
    scanf("%d",&t);
    while(t--)
    {
        init();
        for(int i = 1; i <= n; i++) {
            int factor[10000];
            int cnt=0,sum=0, k = num[i];
            for(int j = 2; k>1 && j <= sqrt(k); j++)
            if(k%j==0) {
                        factor[cnt++] = j;
                        while(k%j==0) {
                             k/=j;
                             sum++;
                         }
            }
            if(k>1) {    //k有可能是质数
                     factor[cnt++]=k;
                     sum++;
           }
           if(sum % 2 == 0) id[num[i]] = (++n1);
           else id[num[i]] = (++n2);
           for(int j = 0; j < cnt; j++)
           {
                int c = num[i]/factor[j];
                if(id[c]) {
                    if(sum&1) g[id[c]].push_back(id[num[i]]);
                    else g[id[num[i]]].push_back(id[c]);
                }
           }
        }
        printf("Case %d: %d\n", ++cas, n - Hmatch());
        for(int i = 1; i <= n1; i++)
            g[i].clear();
    }
    return 0;
}