动态规划之最大子数组和详解

问题

数组子数组的最大和
如arr= [6,-1,3,-4,-6,9,2,-2,5]的最大连续子序列和为14。即为：9,2,-2,5

详解

简单情况

先只考虑，和不会为负数的情况(这样的话起点可以固定下来，最大和的子数组一定是从头开始累计，因为累计的和不会有负数)，例如arr = [6, -1, 3, -4, 9, 2, -2, 5]
代码如下

arr = [6, -1, 3, -4, 9, 2, -2, -5]
n=len(arr)
thisSum=arr[0]      # 记录数组当前累计和
thisSums=[]         # 记录从头开始各项为终点对应的和
for i in range(1, n):
    thisSum += arr[i]
    thisSums.append(thisSum)
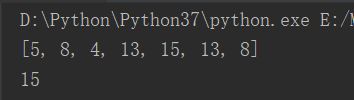
print(thisSums)             # 实际上是6-1=5，6-1+3=8，6-1+3-4=4....
print(max(thisSums))        # 子数组最大的和

运行可得到结果，也就是这个数组的子数组最大和为15。

如果还不明白为什么起点一定从头开始，不妨假设一个子数组T和最大但不从头开始，那么根据和不会为负数，把缺失掉的前面补上应该比子数组T。这就矛盾了，所以一定从头开始。

复杂情况

复杂情况就是起点会在变化，因为累计的过程中，和可能出现负数。一旦出现负数，我们可以丢弃掉这一段，更新起点重新累计。
代码如下

arr = [6, -1, 3, -4, -6, 9, 2, -2, -5]
n=len(arr)
thisSum=arr[0]      # 记录数组当前累计和
thisSums=[]         # 记录各项为终点对应的和
for i in range(1, n):
    if thisSum < 0:         # 增加一个判断，用于更新起点
        thisSum = arr[i]
    else:
        thisSum += arr[i]
    thisSums.append(thisSum)
print(thisSums)             # 实际上是6-1=5，6-1+3=8，6-1+3-4=4， 6-1+3-4-6=-2<0，前面这段丢掉，更新起点从9累计，9+2=11...
print(max(thisSums))        # 子数组最大的和

结果如下

一点优化

上面都是求出了和之后，再求最大值。其实可以在求和的过程中，引入一个变量记录出现的最大值，就不必之后再多遍历一次了。

arr = [6, -1, 3, -4, -6, 9, 2, -2, -5]
n=len(arr)
thisMax = arr[0]
thisSum=arr[0]      # 记录数组当前累计和
for i in range(1, n):
    if thisSum < 0:         # 增加一个判断，用于更新起点
        thisSum = arr[i]
    else:
        thisSum += arr[i]
    # thisSum=max(thisSum+arr[i], arr[i])  # 等价的简化写法
    if thisSum > thisMax:   # 增加一个变量记录出现的最大值
        thisMax = thisSum
    # thisMax = max(thisSum, thisMax)	# 等价的简化写法
print(thisMax)        # 子数组最大的和