【Python】对大数质因数分解的算法问题

发现问题

  我是一个初学者，在编写一个分解质因数的代码时，学习到了 Miller-Rabin素数测试算法 和 Pollard-Rho算法 这两个算法。试着编写了一段代码（下称C1），运行后效果还不错，但感觉好像哪里不对或者还可以优化，于是在网上搜索。最后在百度百科上看到了一段代码（下称C2），同样使用了上述两个算法。
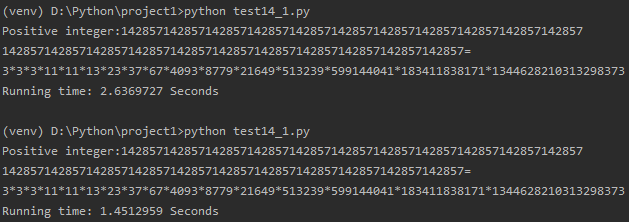
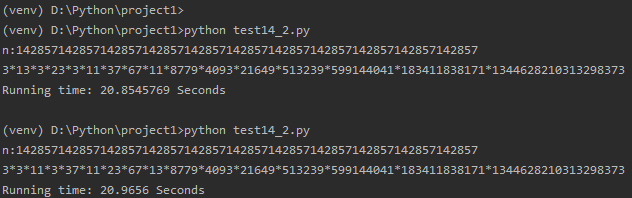
  运行C2后发现，大多数情况下，运行速度差不多。但发现一个数字a，C2的运行时间比C1慢很多。难道我写的算法更优？

数字a为11段1/7的循环节：142857142857142857142857142857142857142857142857142857142857142857

尝试分析

  之后的尝试中，又发现1个数字b，会使得C1陷入死循环。分步解析后得出结论是，卡在了 find(n) 函数上。然后发现最可笑的是输入4无法得出因子2。那应该是我的算法错了吧？
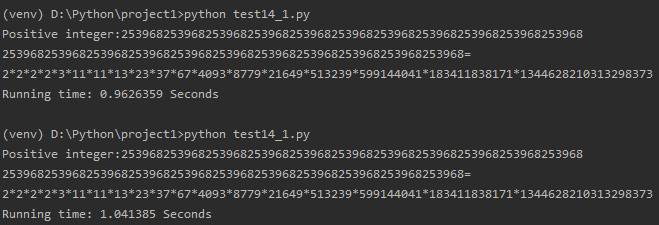
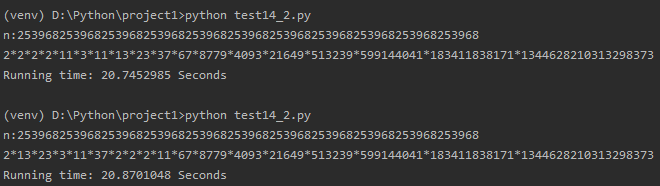
  再去理解了一遍 Pollard-Rho算法 ，发现是因为我定义的 find(n) 函数中使用随机函数 f(x)=x^2+a 无法解出因子2，既然如此，加上一个判定即可解决。

数字b为11段（1/7的循环节+111111）：253968253968253968253968253968253968253968253968253968253968253968

最后

  修复后尝试了一些大数，发现C1确实比C2要快。但我还是不敢确定C1的算法是否正确，还望有人可以指正。
  最后尝试一下数字c，算了好久还以为又死循环了，最后C1都运行了2次了C2还没出结果，无奈ctrl+c。看来对于这种大因子的合数分解，这个算法似乎并不好用。

数字c为费马数2^128+1：340282366920938463463374607431768211457

我的代码（C1）

import math
import random
import time
start = time.perf_counter()


# 判断输入是否为素数
def prime(n):
    if n in {2, 3, 5, 7, 11}:
        return True
    if n % 2 == 0 or n % 3 == 0 or n % 5 == 0 or n % 7 == 0 or n % 11 == 0:
        return False
    t = 0
    u = n - 1
    while u % 2 == 0:
        t += 1
        u //= 2
    a = random.randint(2, n - 1)
    r = pow(a, u, n)
    if r != 1:
        while t > 1 and r != n - 1:
            r = (r * r) % n
            t -= 1
        if r != n - 1:
            return False
    return True


# 寻找输入的一个因数
def find(n, a):
    def f(x):
        return (x * x + a) % n
    
    # 补上因子为2的判定
    if n % 2 == 0:
        return 2
    
    x1 = random.randint(0, n)
    x2 = x1
    while True:
        x1 = f(x1)
        x2 = f(f(x2))
        p = math.gcd(abs(x2-x1), n)
        if p > 1:
            return p
        if x1 == x2:
            return n


num = int(input('Positive integer:'))
print(f'{num}=')

prime_list = []

while num != 1:
    if prime(num):
        prime_list.append(num)
        break
    else:
        c = find(num, random.randint(0, num-1))
        if prime(c):
            prime_list.append(c)
            num //= c

prime_list.sort()
print('*'.join(map(str, prime_list)))

end = time.process_time()
print(f'Running time: {end - start} Seconds')

百科代码（C2）

摘自百度百科分解质因数，我加入了统计运行时间和输出显示。

import random
import time
start = time.perf_counter()


def gcd(a, b):
    if a == 0:
        return b
    if a < 0:
        return gcd(-a, b)
    while b > 0:
        c = a % b
        a, b = b, c
    return a


def mod_mul(a, b, n):
    result = 0
    while b > 0:
        if (b & 1) > 0:
            result = (result + a) % n
        a = (a + a) % n
        b = (b >> 1)
    return result


def mod_exp(a, b, n):
    result = 1
    while b > 0:
        if (b & 1) > 0:
            result = mod_mul(result, a, n)
        a = mod_mul(a, a, n)
        b = (b >> 1)
    return result


def MillerRabinPrimeCheck(n):
    if n in {2, 3, 5, 7, 11}:
        return True
    elif n == 1 or n % 2 == 0 or n % 3 == 0 or n % 5 == 0 or n % 7 == 0 or n % 11 == 0:
        return False
    k, u = 0, n - 1
    while not (u & 1) > 0:
        k += 1
        u = (u >> 1)
    random.seed(0)
    s = 5
    for i in range(s):
        x = random.randint(2, n - 1)
        if x % n == 0:
            continue
        x = mod_exp(x, u, n)
        pre = x
        for j in range(k):
            x = mod_mul(x, x, n)
            if x == 1 and pre != 1 and pre != n - 1:
                return False
            pre = x
        if x != 1:
            return False
        return True


def Pollard_rho(x, c):
    (i, k) = (1, 2)
    x0 = random.randint(0, x)
    y = x0
    while 1:
        i += 1
        x0 = (mod_mul(x0, x0, x) + c) % x
        d = gcd(y - x0, x)
        if d != 1 and d != x:
            return d
        if y == x0:
            return x
        if i == k:
            y = x0
            k += k


def PrimeFactorsListGenerator(n):
    result = []
    if n <= 1:
        return None
    if MillerRabinPrimeCheck(n):
        return [n]
    p = n
    while p >= n:
        p = Pollard_rho(p, random.randint(1, n - 1))
    result.extend(PrimeFactorsListGenerator(p))
    result.extend(PrimeFactorsListGenerator(n // p))
    return result


lis = PrimeFactorsListGenerator(int(input('n:')))
print('*'.join(map(str, lis)))

end = time.process_time()
print(f'Running time: {end - start} Seconds')