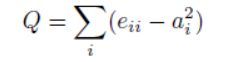静态社区发现——Fast algorithm for detecting community structure in networks

//2019.08.07笔记整理

一、作者 

M.E.J.Newman(再补充)

二、Introduction

1、现在很多网络都呈现社区结构：一些组里面的顶点联系紧密，组与组之间的联系稀疏

2、目前有很多的检测算法，但是这些算法都有很高的计算要求

3、在此前的工作研究：

• Girvan and Newman 提出了一种基于“迭代去除高连接得分的边”的一种计算方法，这种方法对识别“社区”很敏感，被广泛应用在各个网络中。但是该算法计算要求高，最多限制在几千个节点上

（相关论文：

[5] M. Girvan and M. E. J. Newman, Community structure in social and biological networks. Proc. Natl. Acad. Sci.
USA 99, 7821–7826 (2002).
[6] M. E. J. Newman and M. Girvan, Finding and evaluating community structure in networks. Preprint
cond-mat/0308217 (2003).
[7] D.Wilkinson and B. A. Huberman, Finding communities of related genes. Preprint cond-mat/0210147 (2002).
[8] P. Holme, M. Huss, and H. Jeong, Subnetwork hierarchies of biochemical pathways. Bioinformatics 19, 532–
538 (2003).
[9] R. Guimer`a, L. Danon, A. D´ıaz-Guilera, F. Giralt, and A. Arenas, Self-similar community structure in organisa-
tions. Preprint cond-mat/0211498 (2002).
[10] J. R. Tyler, D. M. Wilkinson, and B. A. Huberman, Email as spectroscopy: Automated discovery
of community structure within organizations. Preprintcond-mat/0303264 (2003）.

[11] P. Gleiser and L. Danon, Community structure in jazz.
Preprint cond-mat/0307434 (2003).）

4、基于以上的工作，提出了一种新的检测算法，方法区别于Girvan and Newman(GN)的，但可以得到相似的结果，时间复杂度大大降低（最坏：O(m+n)n，O(N^2)稀疏图；GN的方法O(M^2)N,O(N^2)稀疏图）；同时可以应用到百万级的结点或者更多。

三、算法介绍

1、算法是基于“modularity”的思想

*Modularity是Newman在2003年的论文（“Finding and evaluating community structure in networks” ）中首次提出的，是用来度量自己的社区检测算法的好坏。

*定义1：Consider a particular division of a network into k communities. Let us define a k×k symmetric matrix e whose element  is the fraction of all edges in the network that link vertices in community i to vertices in community j

（博客上说是连接社团i和社团j的边的数目占总边数的比例，同样的eii指的就是社团i的内部的边占总边数的比例）

*模度定义为Q

,其中         i,j都都表示社团

*如果都没有社区的边，那么Q值将为0；然后Q越大（实际中，一般大于0.3认为是存在紧密的社区结构），表示存在很重要的社区结构。

（具体参考：[6] M. E. J. Newman and M. Girvan, Finding and evaluating community structure in networks. Preprint
cond-mat/0308217 (2003).）

2、新思想：基于上面的理论，如果Q越大，代表着一个好的社区划分，那可以简单的优化Q,在所有可能的划分中寻找最优的一个呢？

———》这种思想可以避免迭代删除边并直接切入追逐

———》但是真实的对Q优化又会花费很高

（假设有n个点，g个组，那么划分的方式的数目就是Stirling number的第二种）

*Stirling number（斯特林数）：在组合数学中，可以指两类数；第一类斯特林数表示，将n个不同元素构成m个圆排列(从n个不同元素中不重复的取出m个元素在一个圆周上，叫做n个不同元素的圆排列)的数目，又根据其正负性分为无符号第一类Su(n,m)和带符号第一类Ss（n,m）

*圆排列：区别于排列组合，他没有首尾之分，排成 一个圆圈，那么对于n个人，排成一个圈的话，那对其来说计算公式将是（n-1）!,因为其位置无所谓，那么如果从n中取出m个元素做圆排列，则有

*在此基础上，能划分出的不同的社区的划分种类是