Pascal 定理的严格证明问题
如图，圆锥曲线是一圆，圆内接六边形ABCDEF的边AB、DE的延长线交于点G，边BC、EF的延长线交于点H，边CD、FA的延长线交于点K。
延长AB、CD、EF，分别交直线CD、EF、AB于M、N、L三点，构成△LMN。
直线BC截LM、MN、NL于B、C、H三点，则
…①
直线DE截LM、MN、NL于G、D、E三点，则
…②
直线AF截LM、MN、NL于A、K、F三点，则
…③
连BE，则LA·LB=LF·LE，∴
…④。
同理有： …⑤，
…⑥。
将①②③④⑤⑥相乘，得
。
∵点H、G、K在△LMN的边LN、LM、MN的延长线上，∴H、G、K三点共线。【证明完】
【评论】
1.证明所用圆锥曲线是园；
2.6点ABCDDF在园上的排列方式是依次的顺时针排列；
3.6点ABCDDF在园上的排列的疏密是不同的，其目的是为了看到所有3个对边交点。
4.证明方法是数值演算，一种由Papus在公元前3个世纪就开始使用的方法，非射影几何的方法；
5.只讲一种排列，没有更多的交待，完全看不到Pascal的广泛适用性。
【注】维基上的证明会被不断重新编辑，以上为2014年1月17日见到的证明，现在可能已不同。
2。苏步青先生的证明：
【评论】
1. 这是射影几何的一种典型证明；
2. 所选图形是椭圆；
3. 点的排列次序是135264，即图1中第36个六角形；
4. 提到了椭圆是对应线束决定的曲线；
5. 未作更多交待，也看不到Pascal的广泛适用性。这样的证明方法在射影几何中比较普遍。
3.人教的证明
人教的证明是在 edu6.teacher.com.cn 网上看到的，其证明方法较少见，如下：
定理 圆内接六边形的三对对边的交点共线
【证明】 设是圆，是圆的内接六边形。是六边形三对对边的交点。
由§2.2节球极平面射影性质2（见下面的【附】）知，可取中心射影把圆所在的平面映射到某一平面上，使得变成上的一个圆，直线在此射影下是平面上影消线。
此时有 ，
从而
于是
观察
于是
即直线与相交于无穷远点
所以六边形的三对对边的交点落在上的无穷远直线上
故共线。
【附】球极平面的性质及其预备知识：
§2.2 平面到平面上的中心射影
一、中心射影的定义
1．直线到直线的中心射影：
2．平面到平面的中心投影：
二、无穷远元素
三、透视对应与中心透视
如图1，在引进无穷远元素之后，通过中心射影，把上影消点投影到上无穷远点，把上的无穷远点投影到上影消点。于是中心射影建立了直线之间的一一对应，称这个中心射影为透视对应。
同理，中心射影把平面上的影消线投影到上无穷远直线，同时把上的无穷远直线投影到上影消线。于是中心射影建立了平面到平面间的一一对应，称为平面与之间的中心透视。
中心射影如何改变线段的长度
定理1 设是平面上的四个点，其中任何三点不共线，是平面上的任何三点不共线的四个点，则存在从到的中心（或平行）射影，它把四边形变成与四边形相似的四边形
证明：如图所示
在平面上做与四边形相似的四边形，使得
在空间中移动，使与交于直线
连接，则直线共面
故与的交点就是所求中心射影的射影中心
（如果与平行，则所求中心射影为平行射影）
定理2 设是平面上任意一个多边形，是它的边上或边的延长线上的点，则下面的乘积在中心射影下保持不变。
证明：设与分别是点和在以为中心的中心射影下的像，则由（1）式有
将这些等式两端对应乘积得
四、球极中心射影
（中心射影也可以用来解决包含圆的有关初等几何问题）
设是一球面，是球面上的一点，从球面到它在点处的切平面上的球极平面射影，就是中心在点（点的对径点）的从到的中心射影。
在球极平面射影下，上的任一点（）的像是直线与平面的交点，而点在平面上没有像。
球极平面射影的性质
性质1 球极平面射影把球面上的每一个圆变成平面上的一个圆或一条直线，反之，上的圆或直线的原像是上的圆
性质2 设是平面上的一个圆，是上的不与圆相交的直线，则存在从平面到某个平面的中心射影。它把变成上的圆，并且把直线变成上的无穷远直线。
证明：如图9所示，经过圆在空间做一个球面，并过作一个与球面某点相切的平面。设是平行于平面并与球面相切于点的平面。则与是对径点。
则以为中心的从平面到平面的中心射影，将圆映为平面上圆。将直线映成无穷远直线。
性质3 设是平面上的一个圆，是圆内部的一点，则存在从平面到某一个平面上的中心射影，它把变成平面上的圆。并且把点变成圆的中心。
【评论】
1. 所用圆锥曲线为园；
2. pascal线与园不交；
3. 用到2维的平面投影知识, 而Pascal 定理是2个射影对应一维基本形对应元素生成的图形；
这个要求射影几何知识不少，但证明中又大量利用度量性质。
4. 再要用到复杂的球极平面投影概念，而其关键的性质2（有下划线那一句）的结论明显有误：
除了特例：圆所在平面垂直于球的直径OA，否则， 圆映射到平面上不可能再是一个圆，而是一个椭圆，甚至一段线。
4.利用Desargues逆定理的证法：
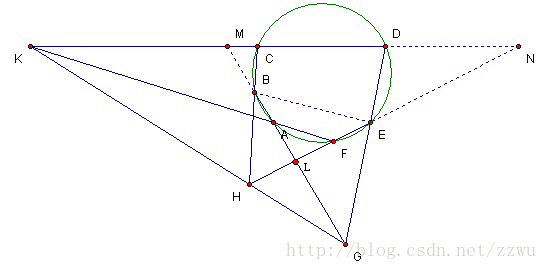
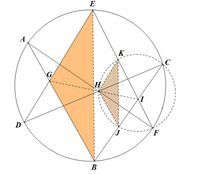
仅对内接于圆的6边形ABCDEF作证明(见下图)。内接于其余2次曲线可由Dedlane定理影射得到。
设G为对边AB与DE交点,H为对边BC与FG交点,I为对边CD与GH交点。作△CHF外接圆交EF于K、BC于J。
∵∠DEF=∠DCF（同圆周角），同样∠DCF=∠HKF，∴∠DEF=∠HKF，故GE∥HK（同位边）
同理可得：HJ∥BG，BE∥KJ
∴△GEB与△HKJ对应边都交于无穷远点；也即这两个三角形3对应边的交点都在无穷远直线上。由此，
根据Desargue定理的逆定理，知△GEB与△HKJ这2三角形对应顶点的连线在一直线上，
即GH、EK、BJ交于一点，此点为I。
∴G、H、I共线，命题得证。
评论：
1.要利用Desargues定理和Dedlan定理，不够直接；
2.未能说明和hexagon的顶点排列形式无关。
5.LEHMER的证明（详细见《射影几何入门》连载4）
2b：用5点不同排列来生成二阶点列，方法都一样；
3.由此，如果ABCDE五点生成了2阶点列为G，在此2阶点列上改变ABCDE五点的位置A'B'C'D'E'，再生成另一 二阶点列为G'，则它就是G;
4.如果在2阶点列G上，除5个生成2阶点列G的点ABCDE之外，另有1点F，则证明ABCDEF一定满足某个关系，这就是PASCAL定理陈述的内容。
4a.根据2a可知，Pascal定理对任意二阶点列都成立，
4b.根据2b可知，对不同排列的6点来生成二阶点列定理都成立。