设计(26) 《PASCAL定理》软件设计
设计(26) 《PASCAL定理》软件设计
![]() 。
。
交互形式的验证不再举例。下面介绍Pascal定理的自动批量验证。
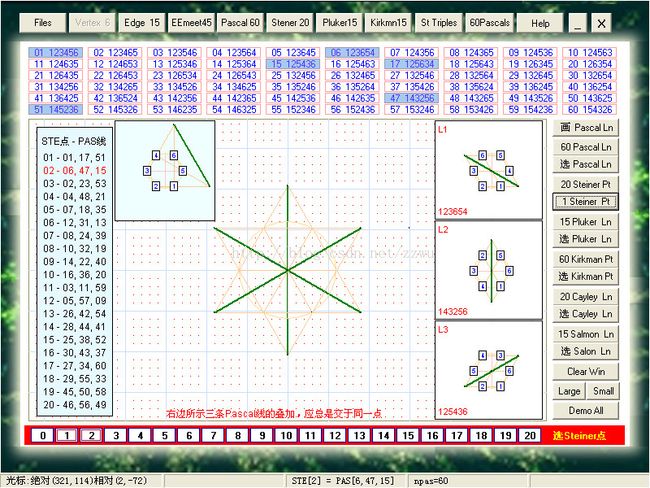
13.8a.以上是译者为考察上述点线关系开发的软件。这里介绍 Steiner定理及其验证。 Steiner定理说:60条 Pascal线分20组、每三条交于一 Steiner点。 底下一行的20个按钮代表要找的Steiner点。点击其中任意按钮在左表中就会查到三个二位数编码, 根据这三个编码可从顶部表中找出三个六边形, 然后在右边三图分别画出这些六边形及对应的Pascal线, 最后在中间的大图中将三个六边形和三条线叠加在一起, 并证明三线交于一点, 此即Steiner点。60条 Pascal线如何划分20组请看下一页的说明, 定理证明请看 http://www.cut-the-knot.org/Curriculum/Geometry/PascalLines.shtml#Explanation
帕斯卡定理
。
及其对400多个特例的验证
0. 这是VOPT软件封面, 但出现仅仅一瞬间即自动消去
0b 上图就是点击屏幕上的
C:六边形菜单后弹出的一个下拉菜单。
1. 以上是概述, 介绍Pascal定理和本软件(Pascal定理验证软件)的功能。定理的证明请参考Lehmer书第4章第60-70节, 或点击菜单定理|射影几何综合法证明,
2. 以上介绍PASCAL定理所涉及的各种圆锥曲线,包括退化的与不退化的圆锥曲线在内共五种。五种曲线上均已选好6点,将用作六边形的顶点。.
【注】 在圆锥曲线上选点可以任意,不影响定理的有效性,我在后面也能让读者自选顶点,但自选顶点通常都使图形质量变差(不对称)。
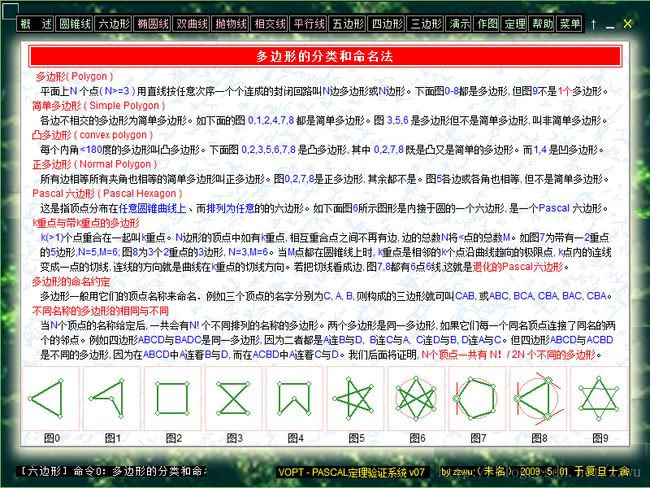
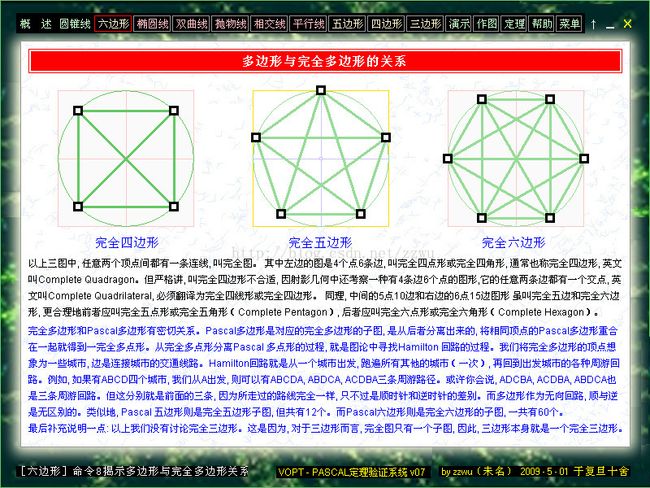
3-0. 以上画面由点击6边形下拉菜单第1项得到,介绍多边形的一般概念,以及与PASCAL定理相关的六边形或多边形的一些例子,如图6图7图8。
【注】为了方便,下面把图7图8类似图形也称六点或六边形,即把k-重点算作k个点,把k-重切线看成k条边。
【注】为了方便,下面把图7图8类似图形也称六点或六边形,即把k-重点算作k个点,把k-重切线看成k条边。
.
3-1. 以上详细介绍神秘的PASCAL六边形或多边形以及它们的命名法(编码法),如123456,123465,135246,等等
3-2. 以上是由6个数字1...6形成的720种排列(字典顺序),每一种排列首尾相接就可形成一个PASCAL六边形,但其中大量是等价的

3-3. 以上是60种不等价的PASCAL六边形,它们都由1,2,3,4,5,6相同的六点组成,但排序不同:从123456直到154326
。
这里值得注意,这60个六边形并非由上720个排列中的最前面的60个排列所形成,必须通过1-1检测才能得到它们,例如,720个排列中第36个为134652,第18个排列为125643,它们只是顺时针与逆时针之间的差别,作为回路实际是等价的,故二者之中只能选择一个。
知道了PASCAL六边形的实际意义后,你也可以这样来产生60个PASCAL六边形:从第1点开始,分别连到其余5点,这有5种选择,以它们为第一边;接下去从剩下的4个点中选择一点,构成第2边,这又有4种可能的选择,....,这样下去,当选择了5条边后就把所有点选完,最后把最后点与第一点连起来构成封闭回路,就成了hexagon了,所以一共有5*4*3*2*1=60种不同选择,即有60个不同的hexagon。
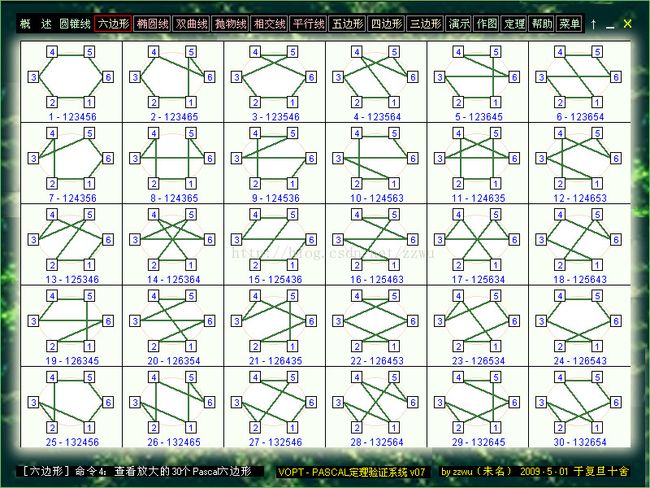
3-4a. 以上是把上面60个图的前30个进行放大显示。
【注意】任意多边形通常是以它们顶点的名称来命名,如以A,B,C三点为顶点的三边形就叫ABC三边形(或ABC三角形)。但点的读出必须依次进行,至于哪一个为首,以及顺时针还是逆时针,都可随便。这种约定使每个N边多边形有2N种叫法。例如三边形ABC有2x3=6种读法,你可叫它ABC,也可叫它CAB, BCA, ...等;上面图中的每个6边形有2x6=12种叫法,如第一个图:123456,可以叫123456,但也可叫234561, 345612, 456123, 561234, 612345,或将6点逆时针地读出来,即称作543216, 432165, 321654, 216543, 165432。这12个顺序的叫法都有权代表图1-123456这个六边形。具有相同顶点的多边形所谓不同,就是它们的顶点的排列次序不同,如图2-123465与图1-123456不同,这二者的差别不是顺逆次序不同或起始点不同。
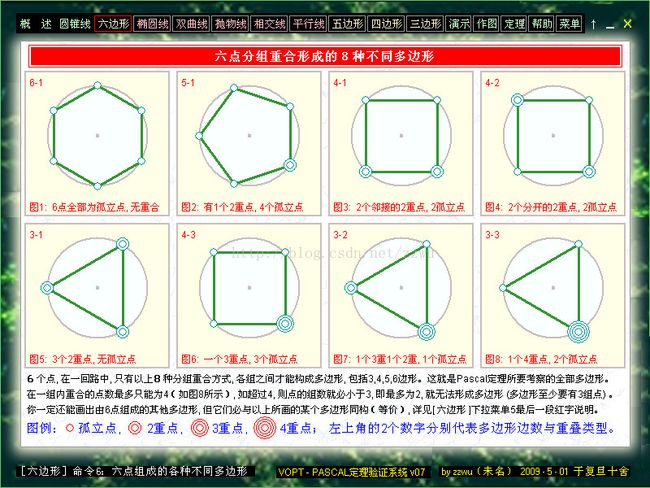
3-6.以上是PASCAL六边形六个点的分布的8个不等价类的图形表示
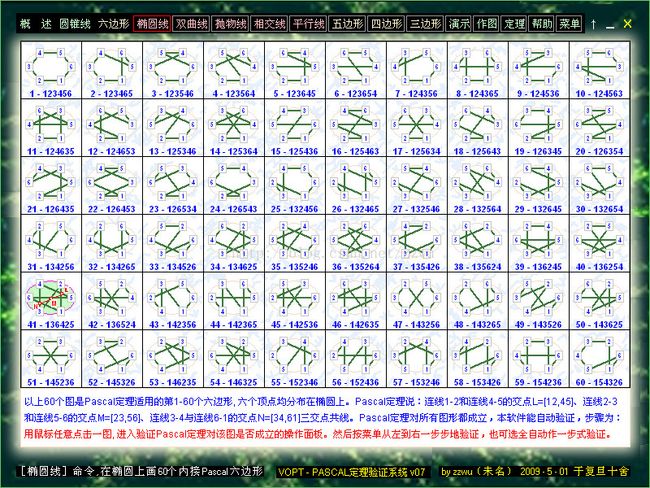
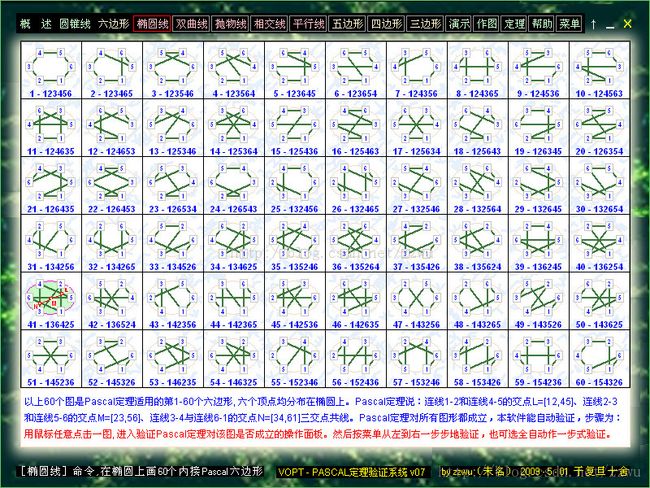
4.以上是内接在椭圆的60个PASCAL六边形,点击其中任意一个,就可进入统一的验证程序(如后面图VP1所示),对该图进行PASCAL定理的验证。
5.以上是内接在双曲线的60个PASCAL六边形.点击其中任意一个,就可进入统一的验证程序,对它进行PASCAL定理的验证
7.以上是6点分布在2条相交直线上的60个PASCAL六边形。点击其中任意一个,就可进入统一的验证程序,对它进行PASCAL定理的验证
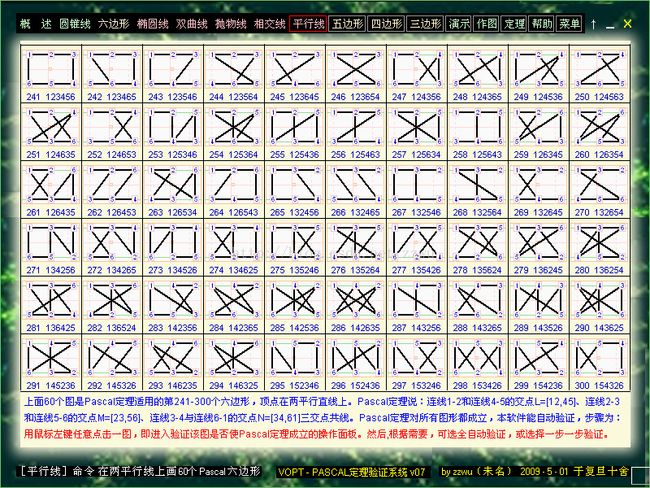
8.以上是6点分布在2条平行直线上的60个PASCAL六边形。点击其中任意一个,就可进入统一的验证程序,对它进行PASCAL定理的验证
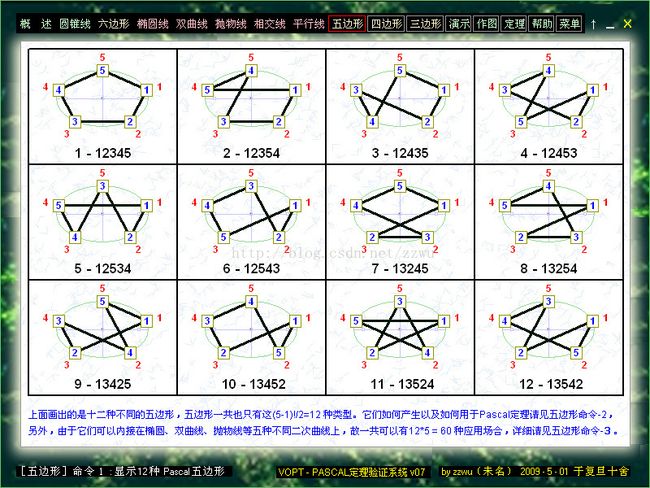
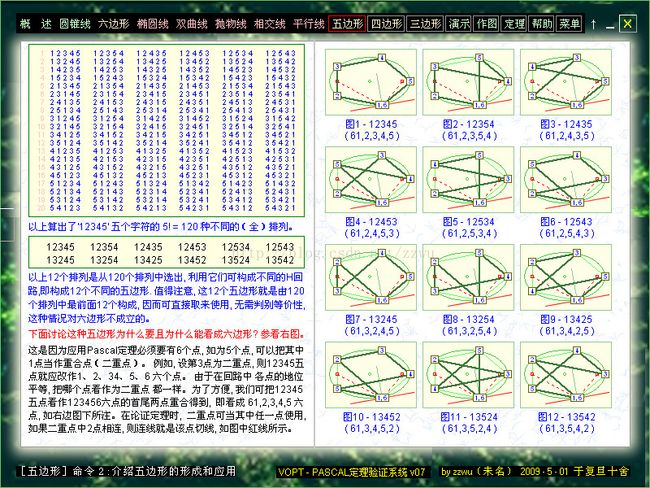
9-2.以上介绍五边形的生成,对五边形应用PASCAL定理需要把其中一点看成2重点,总共凑成6点。2重点中的两个点相连,就是该点的切线
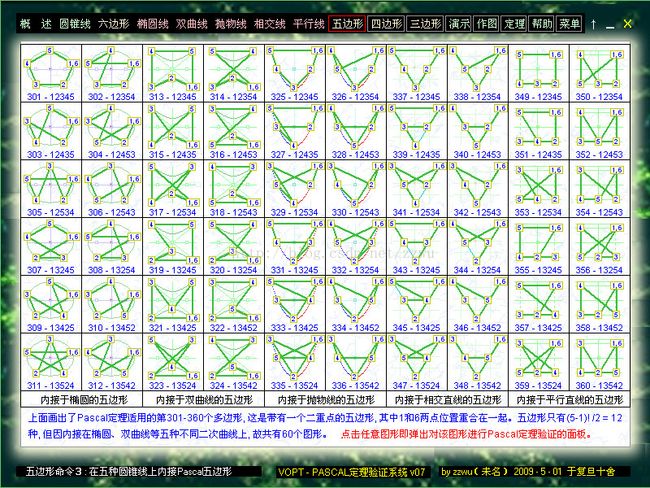
9-3.以上介绍12种五边形内接在5种圆锥曲线形成的60种PASCAL六边形。点击其中任意一个,就可对它进行PASCAL定理的验证
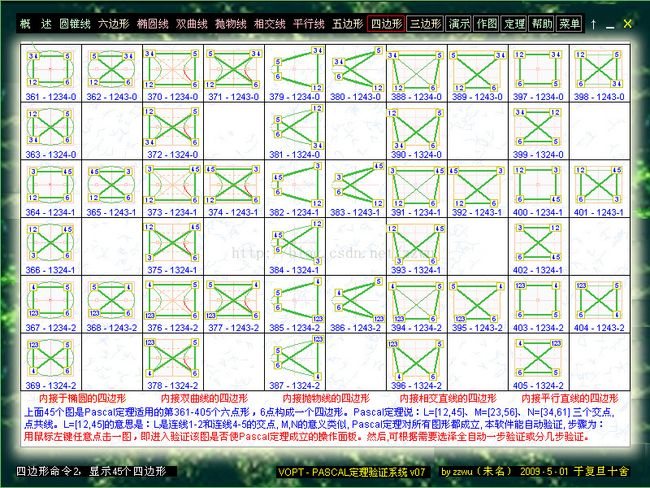
10-1.以上说明不同四边形只有3种,但加入不同的重点后可形成9种PASCAL六边形,再应用于5种圆锥曲线,共有45种不同特例。
.
11. 最后考察三边形,三边形只有1种,但6点重合方式有3种,并可应用于5种曲线类型,所以共有15种Pascal定理适用的多边形,不再细说。
PASCAL六边形的总结:
PASCAL六边形的总结:
这样,我们将各种多边形加起来一共已有了420个(但三边形15个仅画内接于椭圆和抛物线上的6个,所以画出的实际为411个),它们可以带或不带重点,若
将k-重点看成k个点
,
切线看做边
,它们都变成六边形:退化和不退化的Pascal六边形。要证明Pascal定理成立,就必须证明它对所有420个6边形都成立,因420是个有限数字,我们可以对其进行1-1验证。
下面就转来考察如何对上面所列的400多种多边形(包括六边、五边、四边、三边)统一进行PASCAL定理的验证。
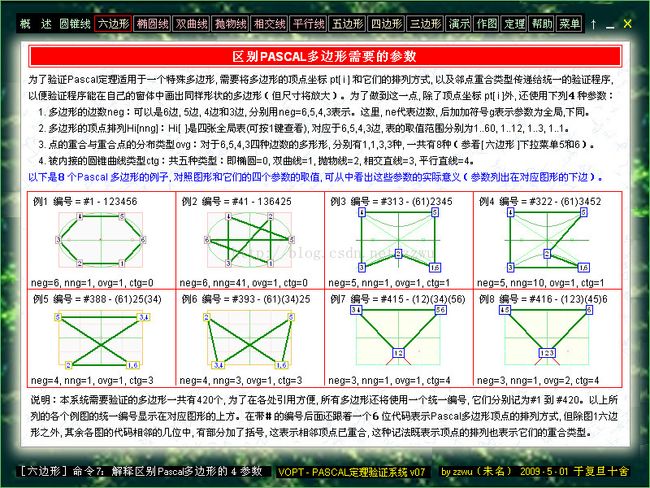
VP1. 以上为PASCAL定理统一验证程序的画面。它能对上面所列的任意多边形进行验证,
验证过程可以按菜单从左到右次序一步一步地步进式进行,也可以全自动地一步完成。
【注】 本窗体(Form2)是点选前面图4~11中某多边形后自动弹出的,无法独立调用。
。
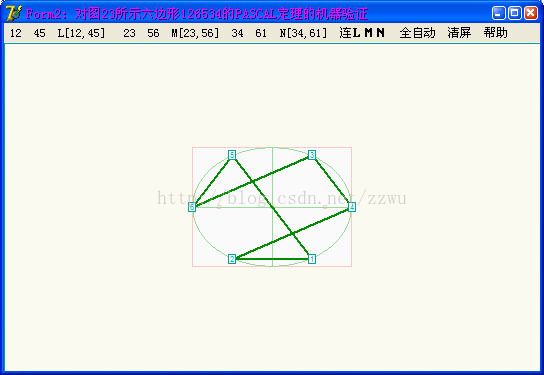
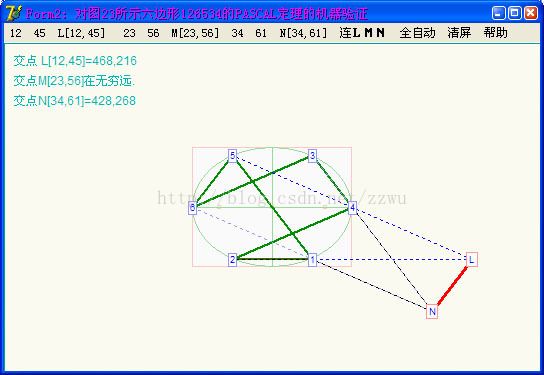
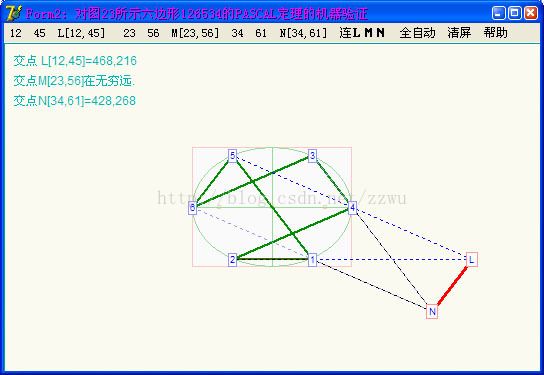
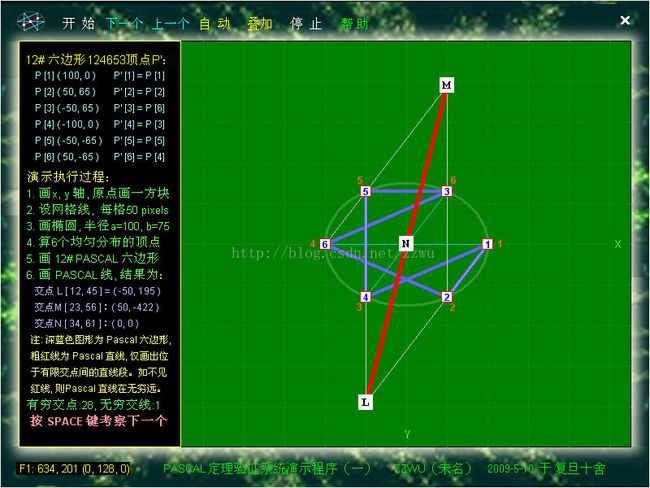
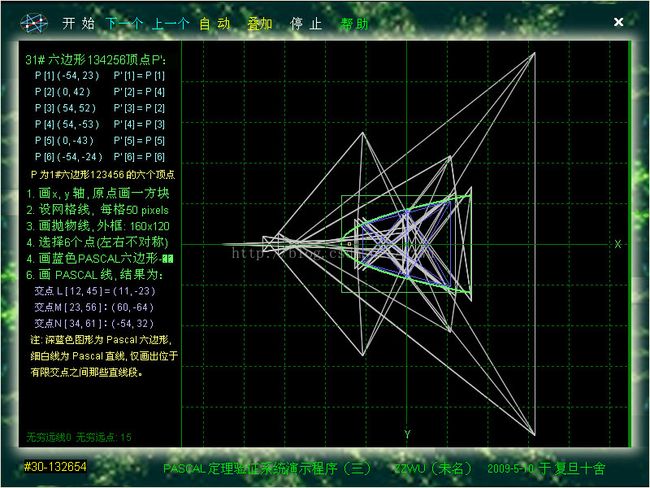
VP2. 以上是对上图(即图4第13六边形)作PACAL定理验证的
结果,3组对边交点L,M,N在一直线上。其中点M为23与56两个平行边之交点在无穷远,实际无法画出来,因这两边与LN也平行,即此无穷远点也LN的交点,如左上角说明。
【注】只要交点M在LN延长线上,在无穷远是允许的,因为这是射影空间的定理。而且还应注意,在无穷远的交点可以是1个也可以是2个或3个。也就是说,有限点不是3个,而只有2个、1个或0个的情况都允许出现。
。
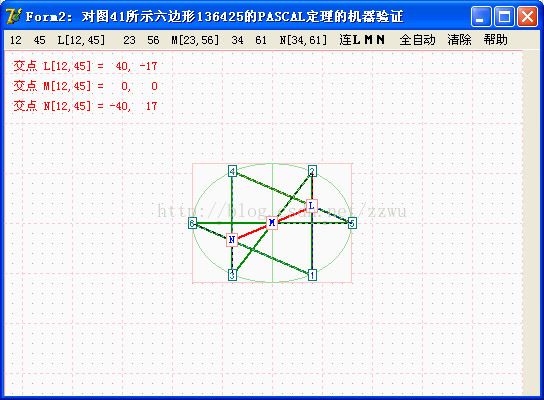
VP3. 以上为对图4中编号为136425的六边形的验证结果,显示3组对边交点L,M,N也在一直线上
。
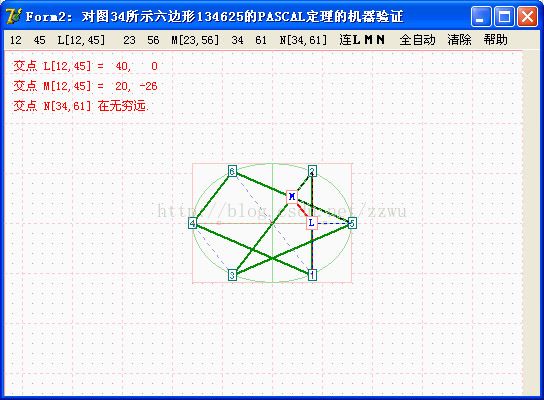
VP4. 以上对图4编号为134625的六边形作PASCAL定理验证,L,M,N在一直线上,但N为ML方向的无穷远点
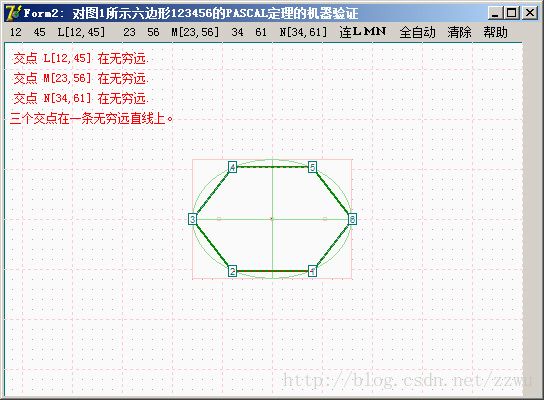
VP5.以上为对图4中编号为123456的六边形的PASCAL定理验证,L,M,N在一直线上,但三点都在无穷远
。
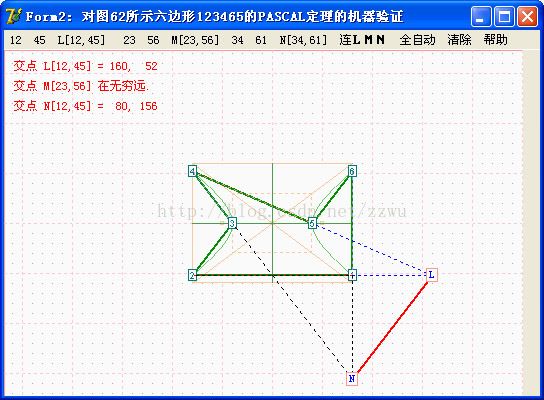
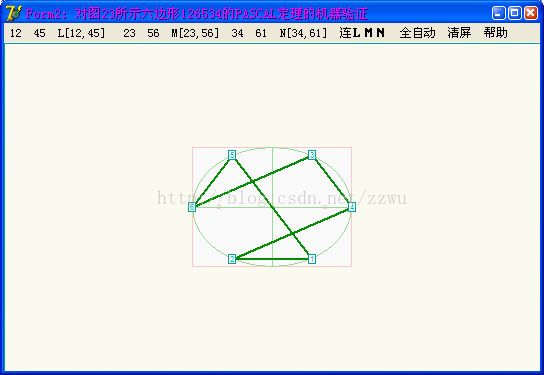
VP6. 以上是对图5中双曲线上123564六边形作PASCAL定理验证,L,M,N在一直线上
。
VP7. 以上是对双曲线上123465六边形的PASCAL定理验证。L,M,N在一直线上,
其中M(23-56交点)是LN方向的无穷远点,无法画出来
。。
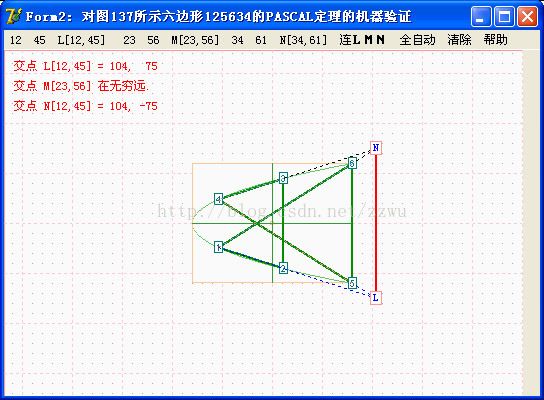
VP8. 以上是对抛物上125634六边形的PASCAL定理验证。L,M,N在一直线上,
M(23-56交点)是LN方向的无穷远点
M(23-56交点)是LN方向的无穷远点
。
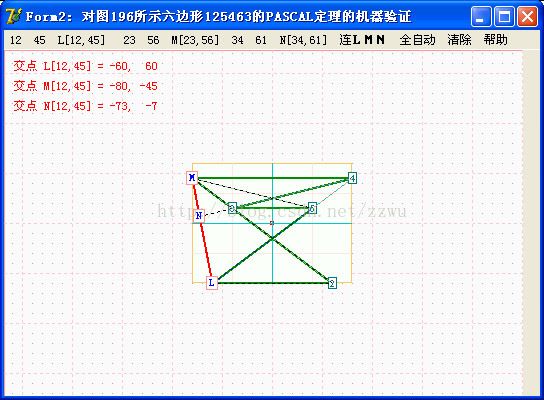
VP9. 以上是对相交直线上125463六边形的PASCAL定理验证。L,M,N在一直线上
。
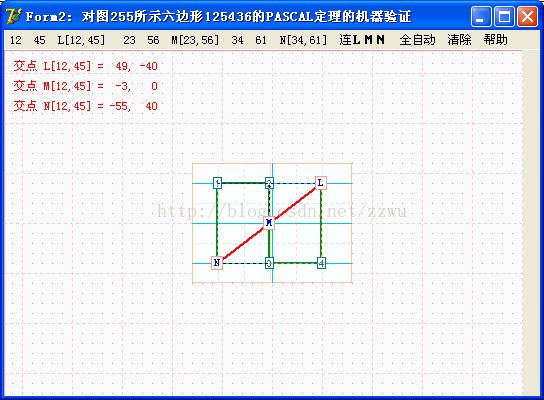
VP10. 以上是对平行线上125436六点构成的六边形的PASCAL定理的验证。L,M,N在一直线上
。.
VP11a. 以上对图9.3中五边形12534作Pascal定理分步验证.已求出L,M,N(N在屏幕外)但未连线。
因其中1点和6点重合在一起构成一个2-重点,故1点与6点的连线是该2-重点的切线。
。。
因其中1点和6点重合在一起构成一个2-重点,故1点与6点的连线是该2-重点的切线。
VP11b. 以上对上图的五边形12534作Pascal定理全自动验证.求出对边交点L,M,N后并又作了连线
其中
12与45的交点L在(-1282,2941),虽然不是无穷远点,但离开屏幕已经很远很远。
最后我们再来看一个图:
VP12.
以上是对
图4的第一个图形、
编号为
123456
的六边形作PASCAL定理的全自动
验证,图形的三组对边分别相互平行,即L,M,N三点均在无穷远!但三组边的三个无穷远点所在的共同直线就是无穷远直线。但三个不同方向的无穷远点怎么会在一条直线上呢?
这有点像地平线,地球上只有一条地平线,同样,
射影平面上只有一条无穷远直线,
这一点可能难于理解,这牵涉到射影几何在欧几里得几何中的的模型问题。这里不详细说明了。
交互形式的验证不再举例。下面介绍Pascal定理的自动批量验证。
12-4.0. 以上是
Pascal 定理自动演示程序-1(封面)。类似程序共有3个,分别对内接于椭圆、双曲线、抛物线的60个六边形进行自动1-1验证
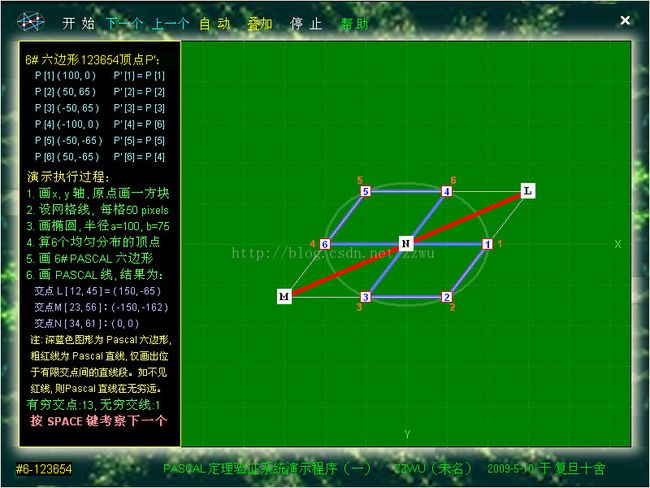
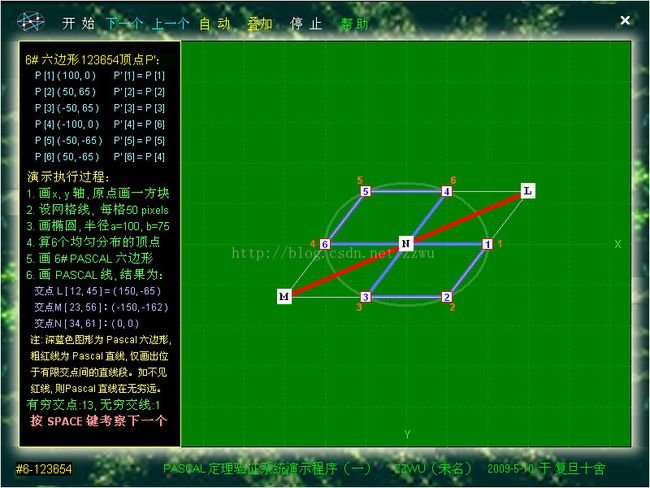
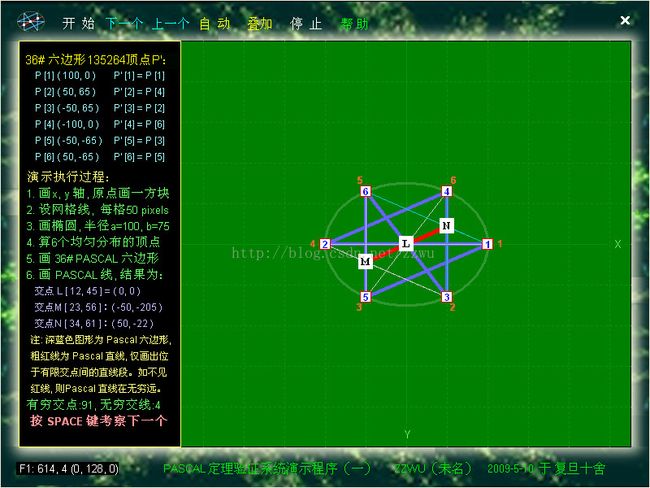
12-4.1.以上是进入Pascal定理自动演示程序(一)后所见的一个画面,红线为PASCAL线
12-4.2.以上是进入Pascal定理自动演示程序(一)所见的另一个画面
,红线为PASCAL线
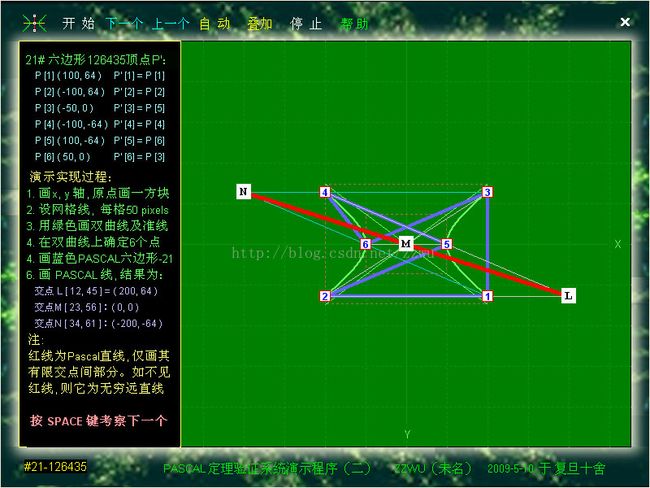
12-4.3. 以上是进入Pascal定理自动演示程序(一)所见的又一个画面,类似地一共有60个画面
12-4.4. 以上是用 Pascal 定理自动演示程序(一)将内接于椭圆的所有60个六边形的Pascal 线叠加在一起显示,这就是一迷魂阵。
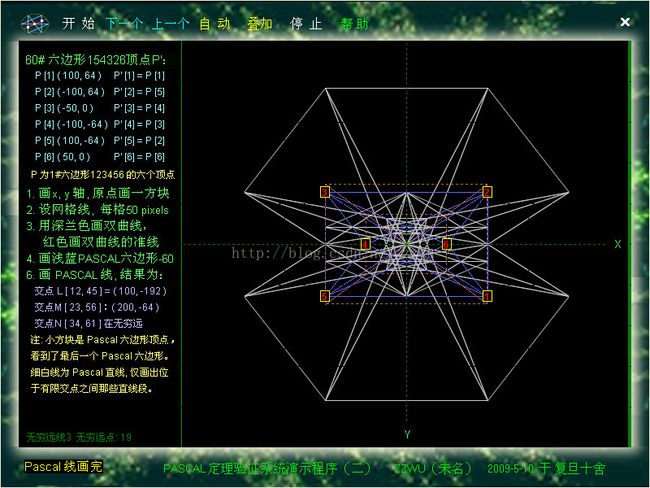
12-5.1. 以上是进入Pascal定理自动演示程序(二)所见的一个画面,类似地可对60个内接于双曲线的六边形进行自动验证
12-5.2. 以上是用 Pascal 定理自动演示程序(二)将双曲线上的六边形的60条Pascal 线叠加在一起显示构成迷魂阵。
12-6.1. 以上是用 Pascal 定理自动演示程序(三)将抛物线上60个六边形的Pascal 线叠加在一起显示构成迷魂阵。
以下进一步讨论和60条PASCAL线有关的点、线和定理。
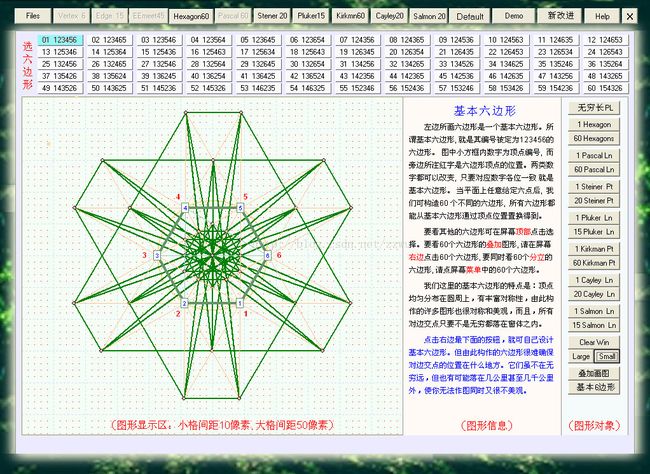
13-7. 另一独立程序。上图是点击右边60 Pascal Ln按钮所得。它也画出了内接于园内基本六边形的60条Pascal线。此图叫PascalHexagrammum Mysticum (Pascal六角迷魂图),可从内接于任意圆锥线的任意6点生成。与此图相关有很多重要概念,包括:Steiner点, Pluker线, Kirkman点, Cayley线, Salmon点。这些点与线的关系可参看下图
(以上图形若因外框限制被缩小,不清晰,请用鼠标点击以上图形,可以放大为1:1的原始尺寸来清晰显示)
.
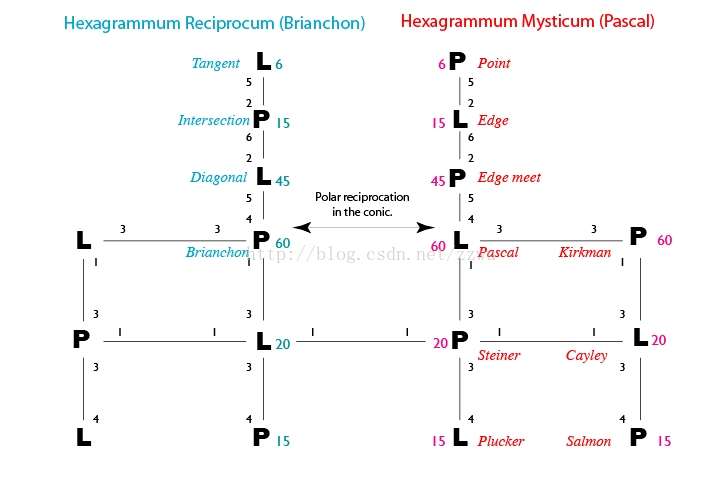
本图右半边,从上到下,由6点出发,依次引出15条边(旁边和下面所注红黑数字6,5,2代表:6个点,每点和其余5点相连,6*5=30边,但要2点形成1边,边数被重复计算,所以6*5后要除2,得到15,才是边的数目。其余意义相同), 45个对边交点(edge meet), 60条Pascal线, 然后分支出20个Steiner点 和 15条Pluker线, 或者. 60个Kirkman点, 20条Cayley线, 15个Salmon点
。图的左半边的线和点 是右半边的点或线的对偶. 例如左边60个Brianchon点是右边60条Pascal线的对偶。要弄清这些点线的概念和相互关系不容易,还有许多定理要了解。可参看网站 http://www.paideiaschool.org/teacherpages/steve_sigur/resources/pascal2/index.html
下面来考察Steiner定理和15个Steiner点,从60条Pascal线到15个Steiner点,中间要经过15个edge和45个edgemeet两步。
下面来考察Steiner定理和15个Steiner点,从60条Pascal线到15个Steiner点,中间要经过15个edge和45个edgemeet两步。

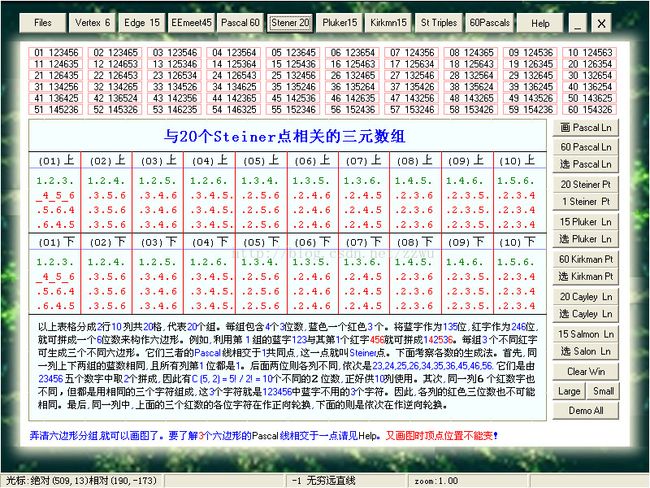
13.8a.以上是译者为考察上述点线关系开发的软件。这里介绍 Steiner定理及其验证。 Steiner定理说:60条 Pascal线分20组、每三条交于一 Steiner点。 底下一行的20个按钮代表要找的Steiner点。点击其中任意按钮在左表中就会查到三个二位数编码, 根据这三个编码可从顶部表中找出三个六边形, 然后在右边三图分别画出这些六边形及对应的Pascal线, 最后在中间的大图中将三个六边形和三条线叠加在一起, 并证明三线交于一点, 此即Steiner点。60条 Pascal线如何划分20组请看下一页的说明, 定理证明请看 http://www.cut-the-knot.org/Curriculum/Geometry/PascalLines.shtml#Explanation
13.8b.以上是
Steiner定理用到的20个三数组的划分方法(详细步骤说明),每一组对应于三条
Pascal线并相交于一个
Steiner点
.
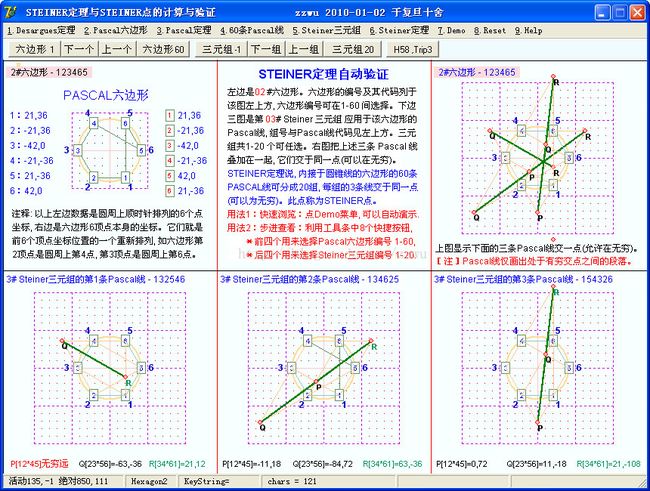
13c. 一个专用于
Steiner定理验证的简单软件。用法及图形的意义见图上部中间一栏的说明。
其余点线不再讨论。下面转来讨论二次曲线作图问题,包括利用或不利用Pascal定理在内。
其余点线不再讨论。下面转来讨论二次曲线作图问题,包括利用或不利用Pascal定理在内。
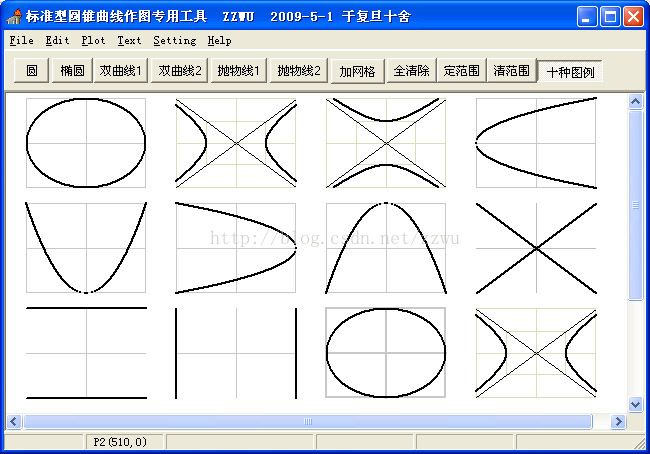
13-0. 以上是圆锥曲线作图法的分类,以及一些具体的作图问题例子,下面将具体介绍两个。
.
13-9.以上是用左上、右下2点交互制作标准型圆锥曲线的程序。其中2条直线(平行或交叉)是代表退化的圆锥曲线
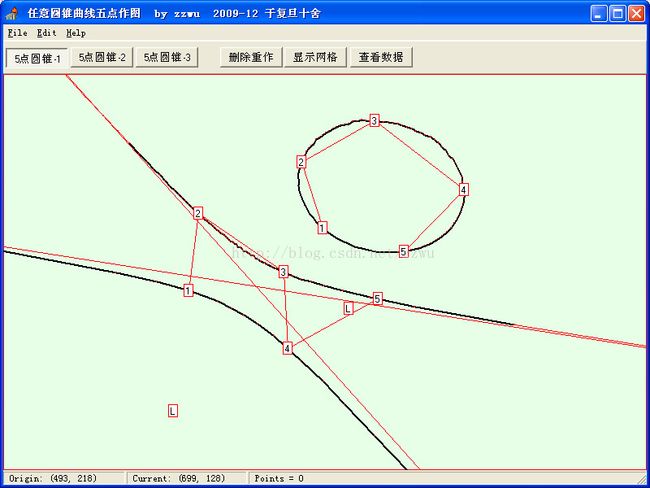
13-10.PASCAL定理重要应用就是作图。以上是接应用PASCAL定理任选五点直接制作的两种圆锥曲线(见Lehmer书上74节)。这些曲线不够光滑,需要改进,一种改进法就是间接作图,即根据5点坐标用Gauss消元法求出圆锥曲线方程,然后就可以像前面画标准圆锥曲线那样,
逐点画出非常精细的曲线。
上图中除了曲线上的 1-5 五点之外,还有两个标有字母 L 的点,它们分别在所作椭圆和双曲线曲线之下,是作图需要的辅助点,详细不再进一步解释。
下面我们转入Pascal定理证明的讨论。
14-2. PASCAL定理证明方法很多,除了书上的射影几何证明方法外,还可以用初等几何法或解析法证明。
初等几何证明法网上可以搜到很多,但证明过程都很繁琐,我们这里不再介绍。上面图中给出的是解析法证明,可以看出,过程很简单,但理解也不容易。另外只是就圆来证明的,一般二次曲线的证明还应利用圆和二次曲线可以射影对应的事实。
【注1】本证明参照网页
http://www.cut-the-knot.org/Curriculum/Geometry/PascalLines.shtml#Explanation翻译得到,,符号有所变动,4个插图为译者所加。
【注2】射影几何证明方法Lehmer 的书上就是,我们这里不再重复,但其实也应补充说明一点:任意二次曲线上对任意Pascal六边形的Pascal定理的证明也可以射影对应,这样才会使读者看了以后感到踏实。后一证明可以参考Cremona的书。
【注2】射影几何证明方法Lehmer 的书上就是,我们这里不再重复,但其实也应补充说明一点:任意二次曲线上对任意Pascal六边形的Pascal定理的证明也可以射影对应,这样才会使读者看了以后感到踏实。后一证明可以参考Cremona的书。
|
返回主页
|
.