在TensorFlow中使用模型剪枝将机器学习模型变得更小

学习如何通过剪枝来使你的模型变得更小

剪枝是一种模型优化技术，这种技术可以消除权重张量中不必要的值。这将会得到更小的模型，并且模型精度非常接近标准模型。

在本文中，我们将通过一个例子来观察剪枝技术对最终模型大小和预测误差的影响。

导入常见问题

我们的第一步导入一些工具、包:

• Os和Zipfile可以帮助我们评估模型的大小。

• tensorflow_model_optimization用来修剪模型。

• load_model用于加载保存的模型。

• 当然还有tensorflow和keras。

最后，初始化TensorBoard，这样就可以将模型可视化:

import os
import zipfile
import tensorflow as tf
import tensorflow_model_optimization as tfmot
from tensorflow.keras.models import load_model
from tensorflow import keras
%load_ext tensorboard

数据集生成

在这个实验中，我们将使用scikit-learn生成一个回归数据集。之后，我们将数据集分解为训练集和测试集:

from sklearn.datasets import make_friedman1
X, y = make_friedman1(n_samples=10000, n_features=10, random_state=0)

from sklearn.model_selection import train_test_split

X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.33, random_state=42)

没有应用剪枝技术的模型

我们将创建一个简单的神经网络来预测目标变量y，然后检查均值平方误差。在此之后，我们将把它与修剪过的整个模型进行比较，然后只与修剪过的Dense层进行比较。

接下来，在30个训练轮次之后，一旦模型停止改进，我们就使用回调来停止训练它。

early_stop = keras.callbacks.EarlyStopping(monitor=’val_loss’, patience=30)

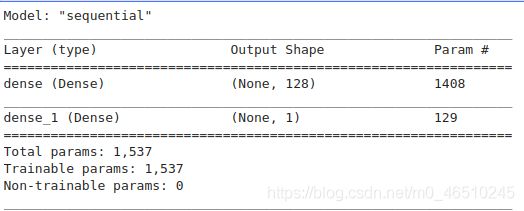
我们打印出模型概述，以便与运用剪枝技术的模型概述进行比较。

model = setup_model()

model.summary()

让我们编译模型并训练它。

tf.keras.utils.plot_model(
 model,
 to_file=”model.png”,
 show_shapes=True,
 show_layer_names=True,
 rankdir=”TB”,
 expand_nested=True,
 dpi=96,
)

现在检查一下均方误差。我们可以继续到下一节，看看当我们修剪整个模型时，这个误差是如何变化的。

from sklearn.metrics import mean_squared_error

predictions = model.predict(X_test)

print(‘Without Pruning MSE %.4f’ %
mean_squared_error(y_test,predictions.reshape(3300,)))

Without Pruning MSE 0.0201

当把模型部署到资源受限的边缘设备（如手机）时，剪枝等优化模型技术尤其重要。

采用等稀疏修剪对整个模型进行剪枝

我们将上面的MSE与修剪整个模型得到的MSE进行比较。第一步是定义剪枝参数。权重剪枝是基于数量级的。这意味着在训练过程中一些权重被转换为零。模型变得稀疏，这样就更容易压缩。由于可以跳过零，稀疏模型还可以加快推理速度。

预期的参数是剪枝计划、块大小和块池类型。

• 在本例中，我们设置了50%的稀疏度，这意味着50%的权重将归零。

• block_size —— 矩阵权重张量中块稀疏模式的维度(高度，权值)。

• block_pooling_type —— 用于对块中的权重进行池化的函数。必须是AVG或MAX。

​

from tensorflow_model_optimization.sparsity.keras import ConstantSparsity
pruning_params = {
    'pruning_schedule': ConstantSparsity(0.5, 0),
    'block_size': (1, 1),
    'block_pooling_type': 'AVG'
}

现在，我们可以应用我们的剪枝参数来修剪整个模型。

from tensorflow_model_optimization.sparsity.keras import prune_low_magnitude
model_to_prune = prune_low_magnitude(
	keras.Sequential([
    tf.keras.layers.Dense(128, activation='relu', input_shape=(X_train.shape[1],)),
    tf.keras.layers.Dense(1, activation='relu')
]), **pruning_params)

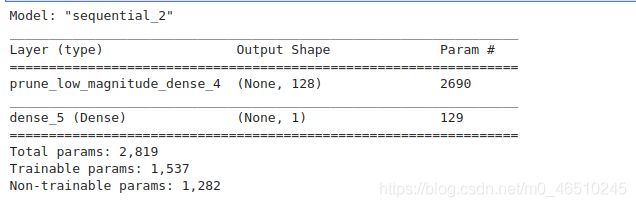
我们检查模型概述。将其与未剪枝模型的模型进行比较。从下图中我们可以看到整个模型已经被剪枝 —— 我们将很快看到剪枝一个稠密层后模型概述的区别。

model_to_prune.summary()

在TF中，我们必须先编译模型，然后才能将其用于训练集和测试集。

model_to_prune.compile(optimizer=’adam’,
 loss=tf.keras.losses.mean_squared_error,
 metrics=[‘mae’, ‘mse’])

由于我们正在使用剪枝技术，所以除了早期停止回调函数之外，我们还必须定义两个剪枝回调函数。我们定义一个记录模型的文件夹，然后创建一个带有回调函数的列表。

tfmot.sparsity.keras.UpdatePruningStep()

使用优化器步骤更新剪枝包装器。如果未能指定剪枝包装器，将会导致错误。

tfmot.sparsity.keras.PruningSummaries()

将剪枝概述添加到Tensorboard。

log_dir = ‘.models’
callbacks = [
 tfmot.sparsity.keras.UpdatePruningStep(),
 # Log sparsity and other metrics in Tensorboard.
 tfmot.sparsity.keras.PruningSummaries(log_dir=log_dir),
 keras.callbacks.EarlyStopping(monitor=’val_loss’, patience=10)
]

有了这些，我们现在就可以将模型与训练集相匹配了。

model_to_prune.fit(X_train,y_train,epochs=100,validation_split=0.2,callbacks=callbacks,verbose=0)

在检查这个模型的均方误差时，我们注意到它比未剪枝模型的均方误差略高。

prune_predictions = model_to_prune.predict(X_test)

print(‘Whole Model Pruned MSE %.4f’ %
 
mean_squared_error(y_test,prune_predictions.reshape(3300,)))

Whole Model Pruned MSE  0.1830

用多项式剪枝计划对稠密层进行剪枝

现在让我们实现相同的模型，但这一次，我们将只剪枝稠密层。请注意在剪枝计划中使用多项式衰退函数。

from tensorflow_model_optimization.sparsity.keras import PolynomialDecay
layer_pruning_params = {
    'pruning_schedule': PolynomialDecay(initial_sparsity=0.2,
    	final_sparsity=0.8, begin_step=1000, end_step=2000),
    'block_size': (2, 3),
    'block_pooling_type': 'MAX'
}

model_layer_prunning = keras.Sequential([
	prune_low_magnitude(tf.keras.layers.Dense(128, activation='relu',input_shape=(X_train.shape[1],)),
						**layer_pruning_params),
						   	 	tf.keras.layers.Dense(1, activation='relu')
    ])

从概述中我们可以看到只有第一个稠密层将被剪枝。

model_layer_prunning.summary()

然后我们编译并拟合模型。

model_layer_prunning.compile(optimizer=’adam’,
 loss=tf.keras.losses.mean_squared_error,
 metrics=[‘mae’, ‘mse’])
model_layer_prunning.fit(X_train,y_train,epochs=300,validation_split=0.1,callbacks=callbacks,verbose=0)

现在，让我们检查均方误差。

layer_prune_predictions = model_layer_prunning.predict(X_test)

print(‘Layer Prunned MSE %.4f’ % 
mean_squared_error(y_test,layer_prune_predictions.reshape(3300,)))

Layer Prunned MSE 0.1388

由于我们使用了不同的剪枝参数，所以我们无法将这里获得的MSE与之前的MSE进行比较。如果您想比较它们，那么请确保剪枝参数是相同的。在测试时，对于这个特定情况，layer_pruning_params给出的错误比pruning_params要低。比较从不同的剪枝参数获得的MSE是有用的，这样你就可以选择一个不会使模型性能变差的MSE。

比较模型大小

现在让我们比较一下有剪枝和没有剪枝模型的大小。我们从训练和保存模型权重开始，以便以后使用。

def train_save_weights():
    model = setup_model()
    model.compile(optimizer='adam',
      loss=tf.keras.losses.mean_squared_error,
      metrics=['mae', 'mse'])
    model.fit(X_train,y_train,epochs=300,validation_split=0.2,callbacks=callbacks,verbose=0)
    model.save_weights('.models/friedman_model_weights.h5')
  
train_save_weights()

我们将建立我们的基础模型，并加载保存的权重。然后我们对整个模型进行剪枝。我们编译、拟合模型，并在Tensorboard上将结果可视化。

base_model = setup_model()
base_model.load_weights('.models/friedman_model_weights.h5') # optional but recommended for model accuracy
model_for_pruning = tfmot.sparsity.keras.prune_low_magnitude(base_model)

model_for_pruning.compile(
    loss=tf.keras.losses.mean_squared_error,
    optimizer='adam',
    metrics=['mae', 'mse']
)

model_for_pruning.fit(
    X_train,
    y_train,
    callbacks=callbacks,
    epochs=300,
    validation_split = 0.2,
    verbose=0
)

%tensorboard --logdir={log_dir}

以下是TensorBoard的剪枝概述的快照。

在TensorBoard上也可以看到其它剪枝模型概述

现在让我们定义一个计算模型大小函数

def get_gzipped_model_size(model,mode_name,zip_name):
    # Returns size of gzipped model, in bytes.
    
    model.save(mode_name, include_optimizer=False)
    
    with zipfile.ZipFile(zip_name, 'w', compression=zipfile.ZIP_DEFLATED) as f:
    f.write(mode_name)
    
    return os.path.getsize(zip_name)

现在我们定义导出模型，然后计算大小。

对于剪枝过的模型，tfmot.sparsity.keras.strip_pruning()用来恢复带有稀疏权重的原始模型。请注意剥离模型和未剥离模型在尺寸上的差异。

model_for_export = tfmot.sparsity.keras.strip_pruning(model_for_pruning)


print("Size of gzipped pruned model without stripping: %.2f bytes" % (get_gzipped_model_size(model_for_pruning,'.models/model_for_pruning.h5','.models/model_for_pruning.zip')))

print("Size of gzipped pruned model with stripping: %.2f bytes" % (get_gzipped_model_size(model_for_export,'.models/model_for_export.h5','.models/model_for_export.zip')))


Size of gzipped pruned model without stripping: 6101.00 bytes
Size of gzipped pruned model with stripping: 5140.00 bytes

对这两个模型进行预测，我们发现它们具有相同的均方误差。

model_for_prunning_predictions = model_for_pruning.predict(X_test)
print('Model for Prunning Error %.4f' % mean_squared_error(y_test,model_for_prunning_predictions.reshape(3300,)))
model_for_export_predictions = model_for_export.predict(X_test)
print('Model for Export Error  %.4f' %  mean_squared_error(y_test,model_for_export_predictions.reshape(3300,)))


Model for Prunning Error 0.0264
Model for Export Error  0.0264

最终想法

您可以继续测试不同的剪枝计划如何影响模型的大小。显然这里的观察结果不具有普遍性。也可以尝试不同的剪枝参数，并了解它们如何影响您的模型大小、预测误差/精度，这将取决于您要解决的问题。

为了进一步优化模型，您可以将其量化。如果您想了解更多，请查看下面的回购和参考资料。

作者：Derrick Mwiti
deephub翻译组：钱三一