图——最小生成树，贪心算法，Prim算法，Kruskal算法

之前我们讲解了加权无向图，但是我们怎样才能找到路径最短的边呢？这就需要最小生成树的知识了。

1.1.1 定义：图的生成树是它的一个含有其所有顶点的无环连通子图，一个加权无向图的最小生成树是它的权值（树中所有边的权值之和）最小的生成树·

1.1.2 树的性质：
1.用一条边连接任意两个顶点都会产生一个环
2.删除树中任意一条边，会得到两棵独立的树。

1.1.3 切分定理
①切分：将图中的所有顶点划分为两个非空且没有交集的集合。
②横切边：连接属于不同集合的顶点的边叫做横切边。
③切分定理：在一幅加权图中，给定任意的切分，横切边中权重最小的边一定属于最小生成树。

注意：权重最小的边不一定是唯一属于最小生成树的，其他边可能在下次切分时，会是权重最小的边。

1.2 贪心算法
贪心算法是计算图的最小生成树的基础算法，它的基本原理就是切分定理。**使用切分定理找到最小生成树的一条边，不断的重复直到找到最小生成树的所有边。**如果图有V个顶点，那么需要找到V-1条边，就可以表示该图的最小生成树。如图所示：


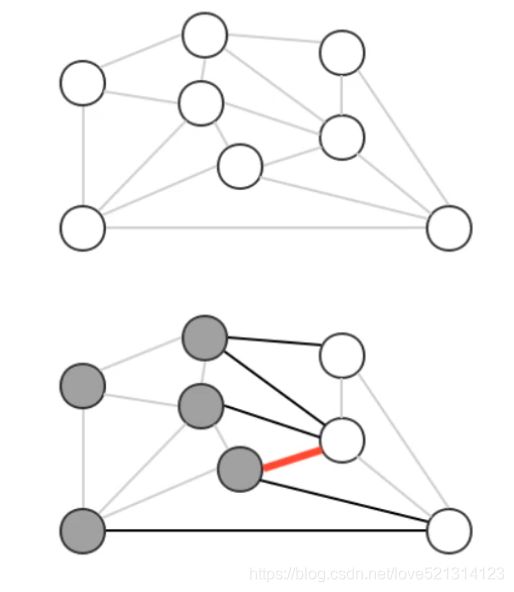
接下来讲的所有算法都是以贪心算法作为基础，所不同的只是保存切分和判定权重最小横切边的方式。

1.3 Prim算法
切分规则：把在最小生成树中的顶点看做一个集合，把不在最小生成树中的其他顶点看成另外一个集合。初始情况下，最小生成树只有一个顶点，然后将权重最小的边以及边所连接的顶点添加到树中，直到添加完所有元素。

构造方法

 //索引代表顶点，值表示当前顶点和最小生成树之间的最短边
    private Edge[] edgeTo;
    //索引代表顶点，值表示当前顶点和最小生成树之间的最短边的权重
    private double[] distTo;
    //索引代表顶点，如果当前顶点已经在树中，则值为true，否则为false
    private boolean[] marked;
    //存放树中顶点与非树中顶点之间的有效横切边
    private IndexMinPriorityQueue<Double> pq;
    //根据一副加权无向图，创建最小生成树计算对象
    public primMST(EdgeWeightedGraph G){
        //初始化成员变量
        this.edgeTo=new Edge[G.getV()];
        this.distTo=new double[G.getV()];
        for (int i = 0; i < distTo.length; i++) {
            distTo[i]=Double.POSITIVE_INFINITY;  //double类型的最大值
        }
        this.marked=new boolean[G.getV()];
        pq=new IndexMinPriorityQueue<Double>(G.getV());
        //默认让0进入最小生成树，但没有和其他顶点相连，所以让distTo对应位置处存储0.0即可
        distTo[0]=0.0;
        pq.insert(0,0.0);
        //遍历索引最小优先队列，拿到最小的边，并添加进最小生成树中
        while(!pq.isEmpty()) {
            visit(G, pq.delMin());
        }
    }

将顶点v添加到最小生成树中，并且更新数据

private void visit(EdgeWeightedGraph G,int v){
        //把顶点v添加到最小生成树中
        marked[v]=true;
        //更新数据
        for (Edge e : G.adj(v)) {
            //获取e边的另外一个顶点
            int w = e.other(v);
            //判断另外一个顶点是否在树中，如果不在，更新数据，如果在，不做任何处理
            if (marked[w]){
                continue;
            }
            else{
                //判断e的权重是否小于从w到树的最小权重
                if (e.getWeight()<distTo[w]){
                    edgeTo[w]=e;
                    distTo[w]=e.getWeight();
                    if (pq.contains(w)){
                        pq.changeItem(w,e.getWeight());
                    }
                    else{
                        pq.insert(w,e.getWeight());
                    }
                }
            }
        }
    }

获取最小生成树的所有边

 public Queue<Edge> edges(){
        //创建队列对象
        Queue<Edge> edges = new Queue<>();
        //遍历edgeTo数组，如果不为null，添加到队列中
        for (int i = 0; i < edgeTo.length; i++) {
            if (edgeTo[i]!=null){
                edges.enqueue(edgeTo[i]);
            }
        }
        return edges;
    }

Prim完整算法

public class primMST {
    //索引代表顶点，值表示当前顶点和最小生成树之间的最短边
    private Edge[] edgeTo;
    //索引代表顶点，值表示当前顶点和最小生成树之间的最短边的权重
    private double[] distTo;
    //索引代表顶点，如果当前顶点已经在树中，则值为true，否则为false
    private boolean[] marked;
    //存放树中顶点与非树中顶点之间的有效横切边
    private IndexMinPriorityQueue<Double> pq;
    //根据一副加权无向图，创建最小生成树计算对象
    public primMST(EdgeWeightedGraph G){
        //初始化成员变量
        this.edgeTo=new Edge[G.getV()];
        this.distTo=new double[G.getV()];
        for (int i = 0; i < distTo.length; i++) {
            distTo[i]=Double.POSITIVE_INFINITY;  //double类型的最大值
        }
        this.marked=new boolean[G.getV()];
        pq=new IndexMinPriorityQueue<Double>(G.getV());
        //默认让0进入最小生成树，但没有和其他顶点相连，所以让distTo对应位置处存储0.0即可
        distTo[0]=0.0;
        pq.insert(0,0.0);
        //遍历索引最小优先队列，拿到最小的边，并添加进最小生成树中
        while(!pq.isEmpty()) {
            visit(G, pq.delMin());
        }
    }
    //将顶点v添加到最小生成树中，并且更新数据
    private void visit(EdgeWeightedGraph G,int v){
        //把顶点v添加到最小生成树中
        marked[v]=true;
        //更新数据
        for (Edge e : G.adj(v)) {
            //获取e边的另外一个顶点
            int w = e.other(v);
            //判断另外一个顶点是否在树中，如果不在，更新数据，如果在，不做任何处理
            if (marked[w]){
                continue;
            }
            else{
                //判断e的权重是否小于从w到树的最小权重
                if (e.getWeight()<distTo[w]){
                    edgeTo[w]=e;
                    distTo[w]=e.getWeight();
                    if (pq.contains(w)){
                        pq.changeItem(w,e.getWeight());
                    }
                    else{
                        pq.insert(w,e.getWeight());
                    }
                }
            }
        }
    }
    //获取最小生成树的所有边
    public Queue<Edge> edges(){
        //创建队列对象
        Queue<Edge> edges = new Queue<>();
        //遍历edgeTo数组，如果不为null，添加到队列中
        for (int i = 0; i < edgeTo.length; i++) {
            if (edgeTo[i]!=null){
                edges.enqueue(edgeTo[i]);
            }
        }
        return edges;
    }
}

1.4 Kruskal算法
kruskal和prim算法的区别：prim算法每次都只为最小生成树添加一条边，而kruskal算法每次都会将两棵树合并为一棵树，直到只剩一棵树为止。

Kruskal算法的实现原理：使用一个MinPriorityQueuepq（最小优先队列）存储图中所有的边，每次使用pq.delMin()取出权重最小的边，并得到该边关联的两个顶点v和w，通过uf.connect(v,w)判断v和w是否已经连通，如果连通，则证明这两个顶点在同一棵树中，那么就不能再把这条边添加到最小生成树中，（因为在一棵树的任意两个顶点上添加一条边，都会形成环，而最小生成树不能有环的存在），如果不连通，则通过uf.connect(v,w)把顶点v所在的树和顶点w所在的树合并成一棵树，并把这条边加入到mst队列（保存最小生成树的所有边）中，这样如果把所有的边处理完，最终mst中存储的就是最小生树的所有边。

Kruskal算法完整代码

public class KruskalMST {
        //保存最小生成树的所有边
        private Queue<Edge> mst;
        //索引代表顶点，使用uf.connect(v,w)可以判断顶点v和顶点w是否在同一颗树中，使用uf.union(v,w)可以把顶点v所在的树和顶点w所在的树
        private UF_Tree_Weighted uf;
        //存储图中所有的边，使用最小优先队列，对边按照权重进行排序
        private MinPriorityQueue<Edge> pq;
        //根据一副加权无向图，创建最小生成树计算对象
        public KruskalMST(EdgeWeightedGraph G){
            //初始化成员变量
            this.mst=new Queue<Edge>();
            this.uf=new UF_Tree_Weighted(G.getV());
            this.pq=new MinPriorityQueue<>(G.getE()+1);
            //把图中所有的边存储到pq中
            for (Edge e : G.edge()) {
                pq.insert(e);
            }
            //遍历pq队列，找到最小权重的边进行处理
            while (!pq.isEmpty()&& mst.size()<G.getV()-1){
                //找到权重最小的边
                Edge e = pq.delMin();
                //找到两个顶点
                int v = e.either();
                int w = e.other(v);
                //判断他们是否在同一棵树中
                if (uf.connected(v,w)){
                    continue;
                }
                uf.nuion(v,w);
                //让e进入mst队列中
                mst.enqueue(e);
            }
        }
        //获取最小生成树的所有边
        public Queue<Edge> edges(){
              return mst;
        }
}

b站详细讲解网址：http://yun.itheima.com/course/639.html