初探多因子选股:多因子筛选与因子正交化
多因子筛选与因子正交化
引言
在多因子研究框架中,如果已经检验出多个有效的因子,而在实际因子选股的过程中,各个有效的因子可能会相互影响,而高度相关的两个有效因子,即使都有不错的获取alpha的能力,但其来源可能相同。
如下图为一系列的资金流向因子和成交额的相关散点图矩阵
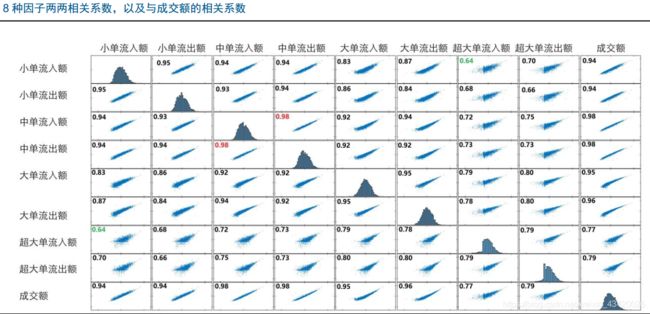
图中资金流向因子与成交额因子都有高度的相关性,存在大量的共同信息是的无法研究各资金流向因子之间的差异。这时就需要正交化方法,将所有资金流向因子与成交额因子正交,正交后的因子可以反映提出成交额后各因子的剩余信息。
何为正交?
考虑一个简单的一元回归模型:
y = b x + ε y=bx+\varepsilon y=bx+ε
假设没有截距项,则其OLS解为:
b = ⟨ x , y ⟩ ⟨ x , x ⟩ b=\frac{\langle x,y\rangle}{\langle x,x\rangle} b=⟨x,x⟩⟨x,y⟩
其中 ⟨ x , y ⟩ \langle x,y\rangle ⟨x,y⟩表示内积,即 ⟨ x , y ⟩ = ∑ x i y i \langle x,y\rangle=\sum x_iy_i ⟨x,y⟩=∑xiyi
将其推广至多因子回归模型:
Y = X b + ε Y=Xb+\varepsilon Y=Xb+ε
假设共有 N N N个股票, K K K个因子
其中 Y Y Y为 N × 1 N\times1 N×1的向量,在多因子模型中表示下一期的收益率,
X X X为 N × K N\times K N×K的当期因子暴露矩阵
b b b为 K × 1 K\times1 K×1的向量,表示因子收益率向量
若在多因子模型中,所有因子都两两正交,即 ⟨ x i , x j ⟩ = 0 , i ≠ j \langle x_i,x_j\rangle=0,i\not =j ⟨xi,xj⟩=0,i=j,则向量 b b b中每一个系数 b i b_i bi恰好等于
b = ⟨ x i , y ⟩ ⟨ x i , x i ⟩ b=\frac{\langle x_i,y\rangle}{\langle x_i,x_i\rangle} b=⟨xi,xi⟩⟨xi,y⟩
证明可以通过OLS的矩阵求解式,这里不多做阐述。从表达式上可以看出,其他因子的因子载荷对因子 i i i的收益率估计不会有任何影响。
从几何看回归中的正交
计算 X X X和 ε \varepsilon ε的内积, b b b用矩阵解析式替换
X T ε = X T ( y − X b ) = X T ( y − X ( X T X ) − 1 X T y ) = X T y − ( X T X ) ( X T X ) − 1 X T y = X T y − X T y = 0 \begin{aligned} X^T\varepsilon &=X^T(y-Xb)\\ &=X^T(y-X(X^TX)^{-1}X^Ty)\\ &=X^Ty-(X^TX)(X^TX)^{-1}X^Ty\\ &=X^Ty-X^Ty\\ &=0 \end{aligned} XTε=XT(y−Xb)=XT(y−X(XTX)−1XTy)=XTy−(XTX)(XTX)−1XTy=XTy−XTy=0
上式说明,在多元回归中,OLS残差项与解释变量正交。
从几何上看(为简单起见先考虑一元回归: y = b x + ε y=bx+\varepsilon y=bx+ε):
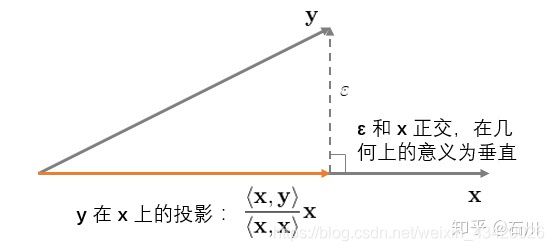
该图可看出回归的本质是将 y y y投影值 X X X上且距离最短(残差平方和最小),这也是OLS的几何意义。
拓展到二元回归: y = b 1 x 1 + b 2 x 2 + ε y=b_1x_1+b_2x_2+\varepsilon y=b1x1+b2x2+ε
假设 x 1 x1 x1与 x 2 x2 x2正交,则:
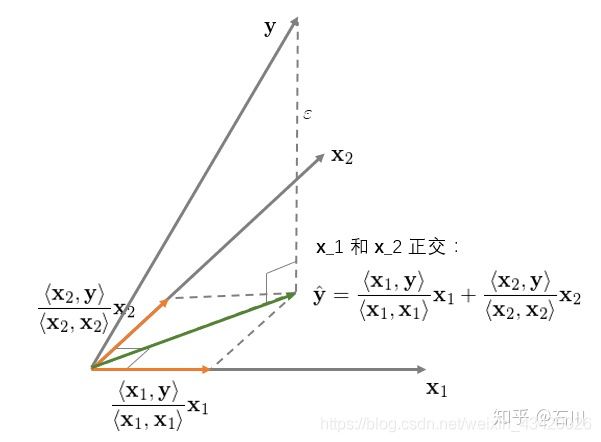
可以,分别将 y y y独立地投影至 x 1 x1 x1与 x 2 x2 x2,生成两条橘黄色向量,由于 x 1 x1 x1与 x 2 x2 x2正交(垂直),故绿色向量是橘黄色向量之和,也是 y y y在平面 x 1 O x 2 x1Ox2 x1Ox2的投影。说明当解释变量互相正交时,不同解释变量的参数估计不会互相影响。
如何对因子正交化
实现因子的正交化,就是要找到一个向量 X o r t h X_{orth} Xorth,与一组给定的基向量 X b a s e X_{base} Xbase正交,即:
X b a s e T X o r t h = 0 X_{base}^TX_{orth}=0 XbaseTXorth=0
回归取残差
上文提到OLS回归后的残差,与解释变量成正比,于是可以通过这种方法将因子正交化,对已知因子回归,通常是Fama因子或barra风格因子。残差即为正交化之后的因子。
Y = X b a s e β + X o r t h O b j e c t i v e f u n c t i o n : a r g m i n X o r t h T X o r t h S . T . X b a s e T X o r t h = 0 β = ( X b a s e T X b a s e ) − 1 X b a s e T Y \begin{aligned} &Y=X_{base}\beta+X_{orth}\\ &Objective \ function: argmin\ X_{orth}^TX_{orth} \\ &S.T.X_{base}^TX_{orth}=0\\ &\beta=(X_{base}^TX_{base})^{-1}X_{base}^TY \end{aligned} Y=Xbaseβ+XorthObjective function:argmin XorthTXorthS.T.XbaseTXorth=0β=(XbaseTXbase)−1XbaseTY
计算 X o r t h X_{orth} Xorth与 Y Y Y的相关系数
c o r r ( Y , X o r t h ) = Y T X o r t h X o r t h T X o r t h = Y T ( Y − X b a s e β ) X o r t h T X o r t h = Y T ( Y − X b a s e ( X b a s e T X b a s e ) − 1 X b a s e T Y ) X o r t h T X o r t h = Y T ( I − X b a s e ( X b a s e T X b a s e ) − 1 X b a s e T ) Y X o r t h T X o r t h = Y T Y X o r t h T X o r t h \begin{aligned} corr(Y,X_{orth})&=\frac{Y^TX_{orth}}{\sqrt{X_{orth}^TX_{orth}}}\\ &=\frac{Y^T(Y-X_{base}\beta)}{\sqrt{X_{orth}^TX_{orth}}}\\ &=\frac{Y^T(Y-X_{base}(X_{base}^TX_{base})^{-1}X_{base}^TY)}{\sqrt{X_{orth}^TX_{orth}}}\\ &=\frac{Y^T(I-X_{base}(X_{base}^TX_{base})^{-1}X_{base}^T)Y}{\sqrt{X_{orth}^TX_{orth}}}\\ &=\frac{Y^TY}{\sqrt{X_{orth}^TX_{orth}}}\\ \end{aligned} corr(Y,Xorth)=XorthTXorthYTXorth=XorthTXorthYT(Y−Xbaseβ)=XorthTXorthYT(Y−Xbase(XbaseTXbase)−1XbaseTY)=XorthTXorthYT(I−Xbase(XbaseTXbase)−1XbaseT)Y=XorthTXorthYTY
故相关系数与残差平方和的平方根成反比,因此回归取残差是满足正交条件下获得因子与原因子相关系数最大的解
Löwdin 对称正交
瑞典物理学家 Löwdin 教授于 1950 年提出对称正交化方法来计算分子轨道。对称正交化的本质是找到一组各列两两相互正交的正交基:
X o r t h T X o r t h = I X_{orth}^TX_{orth}=I XorthTXorth=I
其目标函数为,满足限制条件下,新因子与原有因子的距离(Frobenius范数), X 0 X_0 X0为所有因子构成的因子矩阵
O b j e c t i v e f u n c t i o n : a r g m i n ∥ X o r t h − X 0 ∥ F S . T . X o r t h T X o r t h = I \begin{aligned} &Objective \ function: argmin\ \Vert X_{orth}-X_0\Vert_F \\ &S.T.X_{orth}^TX_{orth}=I\\ \end{aligned} Objective function:argmin ∥Xorth−X0∥FS.T.XorthTXorth=I
可证明其解为将原矩阵做奇异值分解,并将所有奇异值设为1:
X 0 ⟺ s v d U S V T X o r t h = U V T \begin{aligned} &X_0\overset{svd}{\iff} USV^T\\ &X_{orth}=UV^T\\ \end{aligned} X0⟺svdUSVTXorth=UVT
对称正交是将所有因子一起旋转成一组正交基, 但正交后的因子并不与原因子正交:
X o r t h T X 0 = V U T U S V T = V S V T ≠ I X_{orth}^TX_0=VU^TUSV^T=VSV^T\not =I XorthTX0=VUTUSVT=VSVT=I
由于新因子不与原因子正交,而是与旋转后的原因子正交,故其相关性高于回归取残差的结果
部分对称正交
实际应用中我们通常希望新因子相对市值、 beta、波动率等一系列风险因子本身没有暴露,而不是新因子相对旋转后的风险因子没有暴露,即一部分有实际意义的因子不旋转,其它因子无先后顺序地进行对称正交
O b j e c t i v e f u n c t i o n : a r g m i n ∥ X o r t h − X 0 ∥ F S . T . X o r t h T X o r t h = I X b a s e T X o r t h = 0 \begin{aligned} &Objective \ function: argmin\ \Vert X_{orth}-X_0\Vert_F \\ &S.T.X_{orth}^TX_{orth}=I\\ &\ \ \ \ \ \ \ \ X_{base}^TX_{orth}=0 \end{aligned} Objective function:argmin ∥Xorth−X0∥FS.T.XorthTXorth=I XbaseTXorth=0
旋转后的 X o r t h X_{orth} Xorth各列两两正交,且与 X b a s e X_{base} Xbase正交,可证明其解为:
X 0 − X b a s e β = ( 1 − P b a s e ) X 0 ⟺ s v d U ~ S ~ V ~ T P b a s e = X b a s e ( X b a s e T X b a s e ) − 1 X b a s e T X o r t h = U ~ V ~ T \begin{aligned} &X_0-X_{base}\beta=(1-P_{base})X_0\overset{svd}{\iff} \tilde{U}\tilde{S}\tilde{V}^T\\ &P_{base}=X_{base}(X_{base}^TX_{base})^{-1}X_{base}^T\\ &X_{orth}=\tilde{U}\tilde{V}^T \end{aligned} X0−Xbaseβ=(1−Pbase)X0⟺svdU~S~V~TPbase=Xbase(XbaseTXbase)−1XbaseTXorth=U~V~T
正交效果
仍以引言中的例子,各资金流量因子与barra风格因子正交,获得正交后因子,下图为正交前后,大单流入额与小单流入额的相关系数:
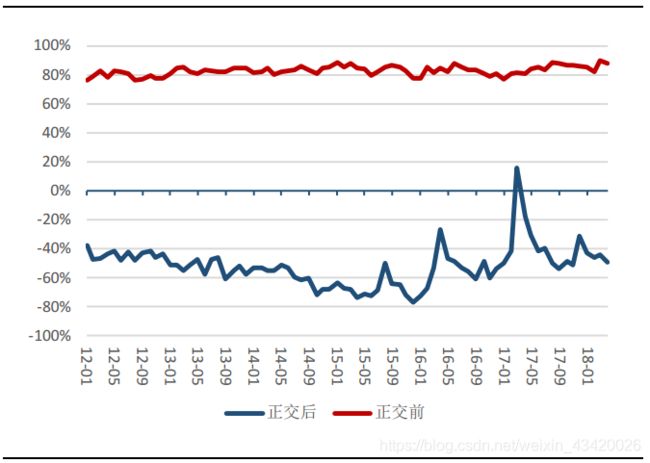
由图可见,在正交化之前,大单流入额与小单流入额包含大量公共信息,即成交额信息,故其具有高度相关性,因为他们很大程度上与成交额共线。正交化之后,呈现负相关,更加合乎因子本身逻辑,在成交额相对不变的前提下,小散资金增多(小单流入额),牛散机构资金便会减少(大单流入额)。
正交化因子表现如下:

可以看出,正交化之后,在剔除公共的成交额信息,超大单和中单相关因子便无法提供信息增量,而大单具有正IC值,小单具有负IC值。符合基本逻辑。机构牛散投资的股票表现普遍好于小散投资的股票。这也有助于因子的筛选,选取有信息增量的因子,而剔除没有信息增量的因子。
风险提示
本文所用例子为介绍正交方法和表现所用,无任何投资参考价值
参考
为什么要进行因子正交化处理?——石川
《长江证券-金融工程专题-邓越-谁是“聪明钱”?资金流因子全面测试兼正交化方法详解》