2019 icpc 沈阳网络赛

比赛上我做出的题

C. Dawn-K’s water

代码：

#include 
#include 
#include 

using namespace std;
typedef long long ll;

const int N = 1e3 + 10;
const int M = 2e4 + 10;

int n, m;
ll f[M];
struct Node {
	int p, c;
} node[N];

bool cmp (Node a, Node b) {
	return a.c < b.c;
}

int main () {
	while (~scanf("%d%d", &n, &m)) {
		for (int i = 0; i < n; i++) {
			scanf("%d%d", &node[i].p, &node[i].c);
		}
		sort(node, node + n, cmp);
		memset(f, 0x3f, sizeof(f));
		f[0] = 0;
		int i = 0;
		for (i = 0; i < n && node[i].c < m; i++) {
			for (int j = 0; j < m; j++) {
				f[j + node[i].c] = min(f[j + node[i].c], f[j] + node[i].p);
			}
		}
		ll a = 1e18;
		int b;
		for (int j = 2 * m - 2; j >= m; j--) {
			if (f[j] < a) {
				a = f[j];
				b = j;
			}
		}
		for (; i < n; i++) {
			if (node[i].p < a || (node[i].p == a && node[i].c > b)) {
				a = node[i].p;
				b = node[i].c;
			}
		}
		printf("%lld %d\n", a, b);
	}
	return 0;
}

D. Fish eating fruit

#include 
#include 

using namespace std;

typedef long long ll;

const int mod = 1e9 + 7;
const int N = 1e4;

ll d[N][3], f[N][3], ans[3];
int cnt[N][3];
bool vis[N];
int n;
int head[N], Next[N * 2], edge[N * 2], len[N * 2], tot = 0;

void clear () {
	tot = 0;
	memset(head, -1, sizeof(head));
	memset(d, 0, sizeof(d));
	memset(f, 0, sizeof(f));
	memset(vis, 0, sizeof(vis));
	memset(cnt, 0, sizeof(cnt));
	memset(ans, 0, sizeof(ans));
}

void add (int a, int b, int c) {
	tot++;
	Next[tot] = head[a];
	head[a] = tot;
	edge[tot] = b;
	len[tot] = c;
}

// f记录到叶子的距离, cnt是分支个数 
void dfs (int x) {
	vis[x] = true;
	for (int i = head[x]; i != -1; i = Next[i]) {
		int y = edge[i], l = len[i];
		if (vis[y]) continue;
		dfs(y);
		for (int j = 0; j < 3; j++) {
			for (int k = 0; k < 3; k++) {
				if (cnt[x][j] == 0 || cnt[y][k] == 0) continue;
				d[x][(j+k+l)%3]=(d[x][(j+k+l)%3]+cnt[y][k]*f[x][j]+cnt[x][j]*f[y][k]+(((ll)cnt[x][j]*cnt[y][k])%mod)*l)%mod;
			}
		}
		for (int j = 0; j < 3; j++) {
			f[x][(j+l)%3] = (f[x][(j+l)%3] + f[y][j] + (ll)cnt[y][j]*l) % mod;
		}
		for (int j = 0; j < 3; j++) {
			cnt[x][(j+l)%3] += cnt[y][j];
		}
	}
	cnt[x][0]++;
}

int main () {
	while (~scanf("%d", &n)) {
		clear();
		int a, b, c;
		for (int i = 1; i < n; i++) {
			scanf("%d%d%d", &a, &b, &c);
			add(a, b, c);
			add(b, a, c);
		}
		dfs(0);
		for (int i = 0; i < n; i++) {
			for (int j = 0; j < 3; j++) {
				ans[j] = (ans[j] + d[i][j] + f[i][j]) % mod;
			}
		}
		printf("%lld %lld %lld\n", (ans[0] * 2) % mod, (ans[1] * 2) % mod, (ans[2] * 2) % mod);
	}
	return 0;
}

F. Honk’s pool

#include  
#include 

using namespace std;

typedef long long ll;

const int N = 5e5 + 10;

int p[N], a[N], b[N], n, n1, n2, k, average;
ll total;

int main () {
	while (~scanf("%d%d", &n, &k)) {
		total = 0;
		for (int i = 0; i < n; i++) {
			scanf("%d", &p[i]);
			total += p[i];
		}
		sort(p, p + n);
		average = total / n;
		for (int i = 0; i < n; i++) {
			if (p[i] < average) {
				a[i] = p[i];
			} else {
				a[i] = average;
				n1 = i;
				break;
			}
		}
		if ((ll)average * n < total) average++;
		for (int i = 0, j = n - 1; j >= 0; j--, i++) {
			if (p[j] > average) {
				b[i] = p[j];
			} else {
				b[i] = average;
				n2 = i;
				break;
			}
		}
		int minv = a[0], maxv = b[0], m;
		for (int i = 0, m = k; i < n1; i++) {
			if (m >= (a[i+1] - a[i]) * (i + 1)) {
				m -= (a[i+1] - a[i]) * (i + 1);
				minv = a[i+1];
			} else {
				minv = a[i] + m / (i + 1);
				break;
			}
		}
		for (int i = 0, m = k; i < n2; i++) {
			if (m >= (b[i] - b[i+1]) * (i + 1)) {
				m -= (b[i] - b[i+1]) * (i + 1);
				maxv = b[i+1];
			} else {
				maxv = b[i] - m / (i + 1);
				break;
			}
		}
		printf("%d\n", maxv - minv);
	}
	return 0;
} 

补题

B

题意
给定一个图。每个节点要么有一个糖果，要么有怪物，只能进一次有怪物的节点，进入怪物节点后会随机走到与怪物相连的任何一个节点。从节点1出发，要求吃尽可能多的糖果。
题解
花了50分钟写完这道题，花了一天找一个bug。所以说细节还是很重要的。写每句代码时，都要思考这句代码的意义是什么。
很简单，计算与节点1直接相连的有糖果的节点，然后计算与节点1相连的怪物节点出去后可以吃的糖果数的期望值的最大值。
代码

#include 
#include 
#include 

using namespace std;

const int N = 1e5 + 10;

int t, n, m, k, ans, num[N], pre[N], moster[N], edgeNum[N];
int head[N], Next[N * 4], edge[N * 4], tot;
int stack[4 * N], top;
bool vis[N], isMoster[N];

void clear () {
	tot = 0;
	ans = 0;
	for (int i = 1; i <= n; i++) {
		pre[i] = i;
		num[i] = 1;
	}
	memset(head, 0, sizeof(head));
	memset(vis, 0, sizeof(vis));
	memset(isMoster, 0, sizeof(isMoster));
	memset(edgeNum, 0, sizeof(edgeNum));
}

void add (int a, int b) {
	tot++;
	Next[tot] = head[a];
	head[a] = tot;
	edge[tot] = b;
	edgeNum[a]++;
}

int find (int x) {
	return x == pre[x] ? x : pre[x] = find(pre[x]);
}

void dfs1 () {
	stack[++top] = 1;
	vis[1] = true;
	while (top > 0) {
		int x = stack[top--];
		num[x] = 0;
		ans++;
		for (int i = head[x]; i; i = Next[i]) {
			int y = edge[i];
			if (vis[y]) continue;
			vis[y] = true;
			if (isMoster[y]) continue;
			stack[++top] = y;
		}
	}
}

void dfs2 (int a) {
	if (vis[a] || isMoster[a]) return;
	stack[++top] = a;
	vis[a] = true;
	while (top > 0) {
		int x = stack[top--];
		for (int i = head[x]; i; i = Next[i]) {
			int y = edge[i];
			if (vis[y] || isMoster[y]) continue;
			vis[y] = true;
			int fx = find(x), fy = find(y);
			pre[fx] = fy;
			num[fy] += num[fx];
			stack[++top] = y;
		}
	}
}

int main () {
	scanf("%d", &t);
	while (t--) {
		scanf("%d%d%d", &n, &m, &k);
		clear();
		int a, b;
		for (int i = 0; i < m; i++) {
			scanf("%d%d", &a, &b);
			add(a, b);
			add(b, a);
		}
		for (int i = 0; i < k; i++) {
			scanf("%d", &moster[i]);
			isMoster[moster[i]] = true;
			num[moster[i]] = 0;
		}
		dfs1();
		double ans2 = 0;
		for (int i = 0; i < k; i++) {
			if (vis[moster[i]]) {
				double val = 0;
				for (int j = head[moster[i]]; j; j = Next[j]) {
					dfs2(edge[j]);
					val += (double)num[find(edge[j])] / edgeNum[moster[i]];
				}
				ans2 = max(ans2, val);
			}
		}
		printf("%.7lf\n", ans2 + ans);
	}
	return 0;
}

G. Special necklace

题意
三角形的任意两个端点的阻值都是2a，棍子的两个端点的阻值都是1a。要求计算n个三角形和n个棍子在一起的时候，点a和点b的阻值。

题解
1、将三角形转换为

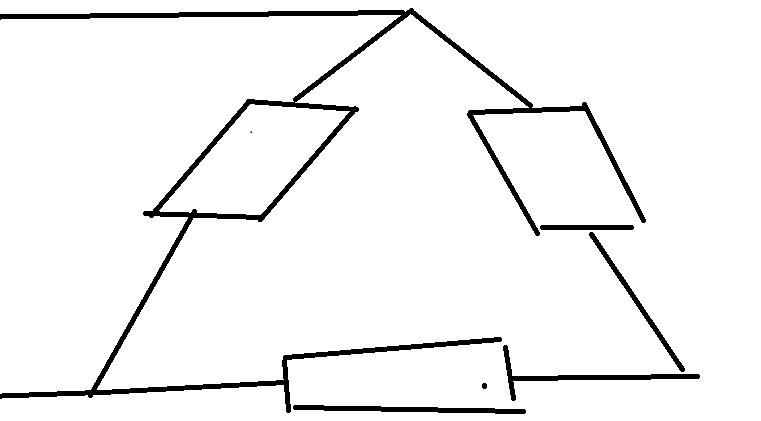
三角形的任意两个端点都为2a，可以计算出每个电阻的大小为3a
2、所以可以将整个礼物的转换成

3、经过计算随着n的增大，a、b之间的电阻变化时越来越小的，直接算，直到a、b之间的电阻不再该表或者以及到达n。

代码

#include 
#include 

using namespace std;

const int N = 1000010;

int t, n;
double a;
char s[N];

void init () {
	int len = strlen(s);
	if (len < 9) {
		n = 0;
		for (int i = 0; i < len; i++) {
			n = n * 10 + s[i] - '0';
		}
	} else {
		n = 1e9;
	}
}

int main () {
	scanf("%d", &t);
	while (t--) {
		getchar();
		scanf("%s%lf", s, &a);
		init();
		int tot = 10;
		double pre, ans = a * 5.0 / 3.0;
		n--;
		a = a * 3;
		while (n-- && tot) {
			pre = ans;
			ans = 1.0/(1.0/a + 1.0 / (a + 1.0 / (1.0/pre + 4/a)));
			if (pre == ans) tot--;
		}
		printf("%.9lf\n", ans);
	}
	
	return 0;
}

J. Ghh Matin

题意
给定n个点，每个点的进入和出去方式都只有一种。求随机一个图,每个点都能经过不超过X的路径回到自己的概率。

题解
1、求P(每个环都小于等于x)比较复杂，我们可以转换成1-P(有一个环的长度大于x)
2、因为2X ≥ N，且每个点的进入和出去的方式都只有一种，所以在图中最多只有一个大于X的环。所以求P(有一个环的长度大于x) = P(存在一个长度为X+1的环) + P(存在一个长度为X+2的环) + … + P(存在一个长度为N的环)
3、
a）在N个节点中选择M个节点的的情况有C(M,N)种。
b）M个节点进行组合数的环形排列有(M-1)!种情况。就相当于固定一个节点，其他M-1个节点进行全排列。
c）N个节点随机排成任意多个节点，有N! 种情况。
所以，P(存在一个长度为M的环) = (C(M, N) × (M-1)! ×(N-M)!) / (N)!。
4、经过转换 P(存在一个长度为M的环) = 1 / m

代码

#include  
#include 

using namespace std;

typedef long long ll;

const int N = 1e6 + 10;
const int mod = 1e9 + 7;

int t, n, x;
ll p[N];

ll quickpow(ll a, ll b) {
    if (b < 0) return 0;
    ll ret = 1;
    a %= mod;
    while (b) {
        if (b & 1) ret = (ret * a) % mod;
        b >>= 1;
        a = (a * a) % mod;
    }
    return ret;
}
ll inv(ll a) {
    return quickpow(a, mod - 2);
}

void init () {
	for (int i = 1; i <= 1e6; i++) {
		p[i] = inv(i);
	}
}

int main () {
	init();
	scanf("%d", &t);
	while (t--) {
		scanf("%d%d", &n, &x);
		ll ans = 0;
		for (int m = x + 1; m <= n; m++) {
			ans = (ans + p[m]) % mod;
		}
		printf("%lld\n", (mod + 1 - ans) % mod);
	}
	return 0;
}

K. Guanguan’s Happy water

题意
有一个长度为n的序列，其中的第1个元素到第2k个元素已知。f[x] = f[x-1] × p[1] + f[x-2] × p[2] + … + f[x-k] × p[k] (k< x)。求 f[1] + f[2] + … + f[n]。

题解
1、
f[k+1] = f[k] × p[1] + f[k-1] × p[2] + … + f[1] × p[k]
f[k+2] = f[k+1] × p[1] + f[k] × p[2] + … + f[1] × p[k]
…
f[2k] = f[2k-1] × p[1] + f[2k-2] × p[2] + … + f[k] × p[k]
k个等式，k个未知数。使用高斯消元可以求出p[1]、p[2]、… 、p[k]
2、后面的推导不太理解，等复习完线性代数，再补上。
代码