数据结构-图-无向图
无向图
一、无向图的说明
1. 稀疏图:有很少边或弧的图;
2. 稠密图:有较多边或弧的图;
3. 网:边/弧带权值的图;
4. 邻接:有边/弧相连的两个顶点之间的关系。存在(Vi,Vj),则称Vi和Vj互为邻接点;
5. 关联(依附):边/弧与顶点之间的关系。存在(Vi,Vj)/
6. 顶点的度:与该顶点相关联的边的数目,记为TD(v);
7. 路径:连续的边构成的顶点序列;
8. 路径长度:路径上边/弧的数目/权值之和;
9. 回路(环):第一个顶点和最后一个顶点相同的路径;
10. 简单路径: 除路径起点和终点可以相同外,其余顶点均不相同的路径;
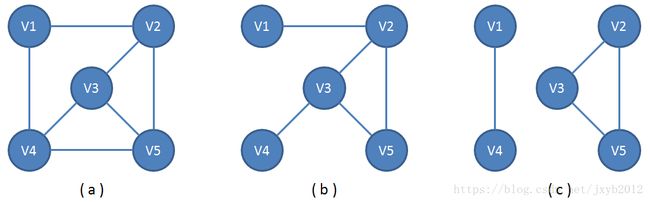
11. 子图:设有两个图 G = (V,{E})、G1 = (V1,{E1}),若 V1 ⊆ V,E1 ⊆ E,则称G1是G的子图;
例:无向图模型中的(b)、(c)是(a)子图;
12. 连通图:在无向图 G = (V,{E})中,若对任意两个顶点v、u都存在从v到u的路径,则称G是连通图;
13. 连通分量:无向图G的极大连通子图称为G的连通分量;
14. 极大连通子图:该子图是G连通子图,将G的任何不在该子图中的顶点加入,子图不再连通;
15. 极小连通子图:该子图是G连通子图,将该子图中删除任意一条边,该子图不再连通;
16. 生成树:包含无向图G所有顶点的极小连通子图;
17. 生成森林:对非连通图,由各个连通分量的生成树的集合;
二、无向图的模型
1. 图 Graph = ( V , E )。
V:顶点(数据元素)的有穷非空集合;
E:边的有穷集合;
2. 每条边都是无方向的。
三、图的定义与操作
1. CreateGraph(&G , V , VR)
初始条件:V是图的顶点集,VR是图中弧的集合;
操作结果:按V和VR的定义构造图G;
2. DFSTraverse(G)
初始条件:图G存在;
操作结果:对图进行深度优先遍历;
3. BFSTraverse(G)
初始条件:图G存在:
操作结果:对图进行广度优先遍历:
程序代码
main.cpp (链表方式)
#include
using namespace std;
#define MVNum 100 //最大顶点数
#define OK 1
typedef char VerTexType; //顶点信息
typedef int OtherInfo; //和边相关的信息
//定义图的邻接表储存类型
typedef struct ArcNode {//边节点
int adjvex; //该边所指向的顶点的位置
struct ArcNode *nextArc; //指向下一条边的指针
OtherInfo info;//和边相关的信息
}ArcNode;
typedef struct VNode {//顶点节点
VerTexType data; //顶点信息
ArcNode *firstArc;//指向第一条依附该顶点的边的指针
}VNode,AdjList[MVNum];
typedef struct {
AdjList vextices;//邻接表
int vexNum, arcNum;//图的顶点数,边数
}ALGraph;
//确定点V在G中的位置
int LocateVex(const ALGraph& G, VerTexType v)
{
for (int i = 0; i < G.vexNum; i++)
{
if (v == G.vextices[i].data)
{
return i;
}
}
return -1;
}
//创建无向图
int CreateUDG(ALGraph &G)
{
int i, k;
cout << "请输入图的顶点 边总数,使用空格隔开:";
cin >> G.vexNum >> G.arcNum;
cout << endl;
cout << "请输入顶点的名称 : 如 A" << endl;
for (i = 0; i < G.vexNum; i++)
{
cout << "请输入第" << (i + 1) << "个顶点的名称:";
cin >> G.vextices[i].data;
G.vextices[i].firstArc = NULL;
}
cout << endl;
cout << "请输入一条依附顶点的边,如 A B" << endl;
for (k = 0 ; k < G.arcNum; k++)
{
VerTexType v1, v2;
int m, n;
cout << "请输入第" << (k + 1) << "条边依附的顶点:";
cin >> v1 >> v2;
//v1 v2在G中的位置
m = LocateVex(G, v1); // A 0
n = LocateVex(G, v2); // B 1
//生成一个新边节点
ArcNode *p1 = new ArcNode;
p1->adjvex = n;
p1->nextArc = G.vextices[m].firstArc;
G.vextices[m].firstArc = p1;
//生成一个新边节点
ArcNode *p2 = new ArcNode;
p2->adjvex = m;
p2->nextArc = G.vextices[n].firstArc;
G.vextices[n].firstArc = p2;
}
return OK;
}
int main(int argc, char** argv)
{
cout << "邻接表创建无向图" << endl << endl;
ALGraph G;
CreateUDG(G);
cout << endl;
for (int i = 0 ; i < G.vexNum; i++)
{
VNode temp = G.vextices[i];
ArcNode *p = temp.firstArc;
if (p == NULL)
{
cout << G.vextices[i].data << endl;
}
else
{
cout << temp.data;
while (p)
{
cout << "->";
cout << p->adjvex;
p = p->nextArc;
}
}
cout << endl;
}
system("pause");
return 0;
}