机器学习第二篇：逻辑回归

逻辑回归（Logistic Regression）

本质上讲，机器学习就是一个模型对外界的刺激（训练样本）做出反映，趋利避害（评价标准）。

目录

1、 逻辑回归的原理
2、逻辑回归与线性回归的联系与区别
3、逻辑回归损失函数推导及优化
4、 正则化与模型评估指标
5、逻辑回归的优缺点
6、样本不均衡问题解决办法
7. Sklearn参数浅析

逻辑回归原理？

逻辑回归是一种有监督的统计学习方法，主要是对样本进行分类。
逻辑回归就是这样的一个过程：面对一个回归或者分类问题，建立代价函数，然后通过优化方法迭代求解出最优的模型参数，然后测试验证我们这个求解的模型的好坏。Logistic回归虽然名字里带“回归”，但是它实际上是一种分类方法，主要用于两分类问题（即输出只有两种，分别代表两个类别）回归模型中，y是一个定性变量，比如y=0或1，logistic方法主要应用于研究某些事件发生的概率。

逻辑回归与线性回归的联系与区别？

区别：

线性回归的输出连续的，即对于每输入的一个x，都有对应的一个y输出，模型的定义域和值域都可以是【−∞，+∞】，但是对于逻辑回归，输入可以是连续的【−∞，+∞】，但是输出一般是离散的，即只有有限个输出值。例如，其值域可以是只有两个值{0，1}，这两个值可以表示对样本的某种分类，高/低，患病/健康等等，这就是常见的二分类逻辑回归。因此，从总体上说，通过逻辑回归，我们将在整个实数范围映射到有限个点上，这样就实现了对x的分类，因为每次拿过来一个x，经过逻辑回归分析，就可以将他归为某一类中。

联系：

逻辑回归也被称为广义线性回归模型，他与线性回归模型的形式基本上相同，都具有(ax+b)，其中a和b都是待求参数，其区别在于他们的因变量不同，多重线性回归直接将ax+b作为因变量，即y=ax+b，而逻辑回归则通过函数S将ax+b对应到一个隐状态p，p=S(ax+b),然后根据p与（1-p）的大小决定因变量的值。这里的函数S是Sigmoid函数。

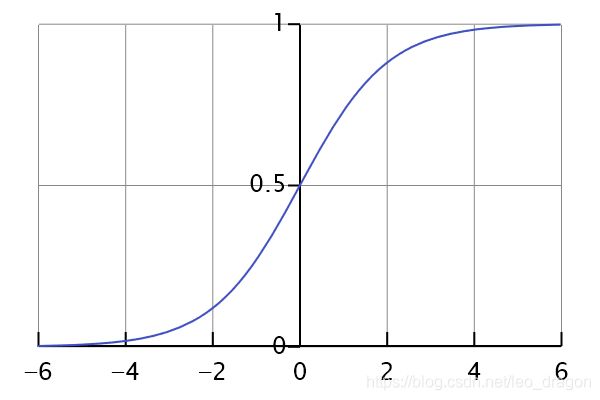
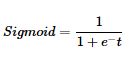
S函数分析，通过S函数的作用，将S函数里面的t表示为（ax+b），则我们输出的值就可以限制在【0，1】区间上，我们上面说的输出y只有两个值，但是这里却出现了【0，1】一个区间。其实真实情况下，我们最终得到的y值是在【0，1】这个区间上的一个数，然后我们可以选择一个阈值，通常是0.5,当y>0.5的时候就将x归为1这一类，其余的就归为0这一类。

逻辑回归损失函数推导及优化

逻辑回归的公式为：

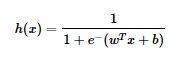
假设有N个样本，样本的标签只有0和1两类，可以用极大似然估计法估计模型参数（啥是极大似然估计？https://blog.csdn.net/class_brick/article/details/79724660 ），从而得到回归模型：
设yi = 1的概率为pi，yi=0的概率是1-pi，那么观测的概率为：

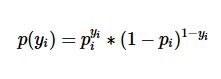
概率由逻辑回归的公式求解，那么代进去得到极大似然函数：

取对数后：

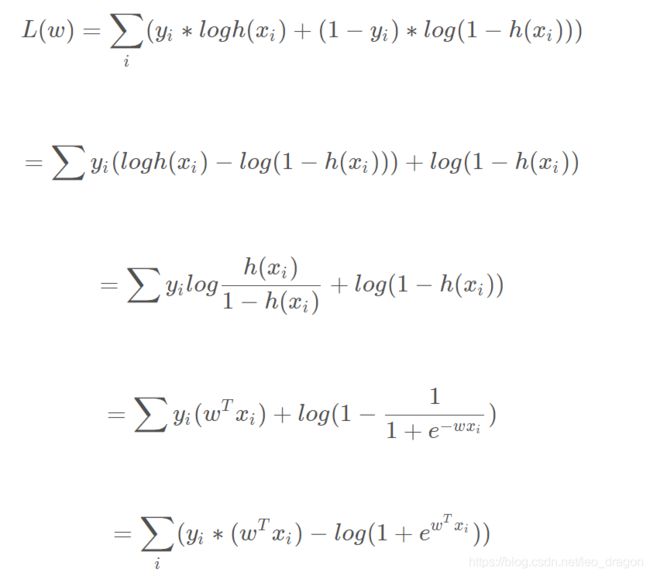
极大似然估计算法的求解步骤：
1、得到所要求的极大似然估计的概率p的范围
2、以p为自变量，推导出当前已知事件的概率函数式Q§
3、求出能使得Q§最大的p
上面的式子的计算过程，对L（w）求极大值以得到w的估计值，其实实际操作中会加个负号，变成最小化问题，通常会采用随机梯度下降法和牛顿迭代法来求解

梯度

由上式求出的损失函数：

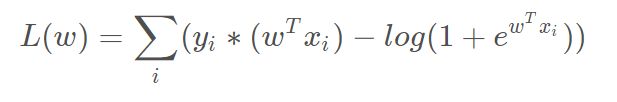
现在开始对w求导：

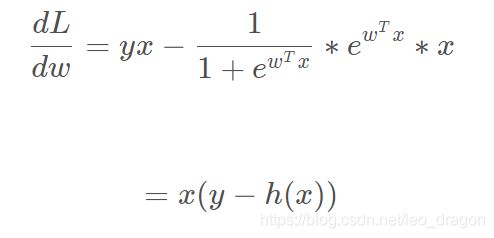
通常来说，是用梯度下降法来求解的，所以会在损失函数前面加个负号求最小值，所以最终的导数变为：
(h(x) -y)x

正则化与模型评估指标

（一）正则化：

正则化是结构风险最小化策略的实现，是在经验风险上加上一个正则化（regularization）或者惩罚项（penalty）。是模型选择的典型方法。正则化项一般是模型复杂度的单调递增函数，模型越复杂，正则化值越大。比较常用的正则化项有模型参数向量的范数，L1，L2等。
过拟合现象（overfitting）：
所谓过拟合，就是特征量冗余，导致拟合函数虽然能够很好的满足训练姐，但是波动性大、方差大、，对于新的样本值不能很好的预测（过犹不及）。

第一个模型是一个线性模型,欠拟合,不能很好地适应我们的训练集;第三个模型是一 个四次方的模型,过于强调拟合原始数据,而丢失了算法的本质:预测新数据。我们可以看 出,若给出一个新的值使之预测,它将表现的很差,是过拟合,虽然能非常好地适应我们的 训练集但在新输入变量进行预测时可能会效果不好;而中间的模型似乎最合适。就以多项式为理解，x的次数越高，拟合得越好，但相应得预测能力就可能变差。如果我们发现了过拟合问题，如何处理：
1、丢弃一些不能帮助我们正确预测的特征。可以是手工选择保留哪些特征，或者使用一些模型选择的算法来帮忙（例如PCA）
2、正则化。保留所有的特征，但是减少参数的大小（magnitude）。

正则化之线性回归：

对于线性回归的求解，一种是基于梯度下降，一种是基于正规方程。
正则化线性回归的代价函数为：

正则化之逻辑回归：

（二）模型评估指示

| TP | True Positive，样本为正，判断为正 |
|TN| True Negative，样本为负，判断为负|
| FP| False Positive，样本为负，判断为正 |
| FN| False Negative，样本为正，判断为负 |
1、用来表示模型预测正确的样本比例
正确率（Accuracy） = （TP+TN）/（TP+TN+FP+FN），即正确的比例除于全部比例
2、精度和召回率：
精度：（查准率）是指正确预测的正样本所占所有预测为正样本的比例
Precision = TP/（TP+FP） 评估的是准确性
召回率：（查全率）又称为灵敏度和命中率，是指正样本被正确预测的比例：
Recall = TP/（TP+FN） FN表示，正样本，但是被预测为负样本了。评估的是覆盖率
3、F1值：
精度和召回率是负相关的：高精度往往对应低召回率，可以这样理解：覆盖率越高，精度越低
F1值是综合考虑精度和召回率的一个指标：
F1 = 2*（精确率*召回率）/（精确率+召回率）

逻辑回归的优缺点

优点：
（模型）模型清晰，背后的概率推导经得住推敲。
（输出）输出值自然地落在0到1之间，并且有概率意义
（参数）参数代表每个特征对输出的影响，可解释性强。
（简单高效）实施简单，非常高效（计算量小、存储占用低），可以在大数据场景中使用。
（可扩展）可以使用online learning的方式更新轻松更新参数，不需要重新训练整个模型。
（过拟合）解决过拟合的方法很多，如L1、L2正则化。
（多重共线性）L2正则化就可以解决多重共线性问题。
缺点：
（特征相关情况）因为它本质上是一个线性的分类器，所以处理不好特征之间相关的情况。
（特征空间）特征空间很大时，性能不好。
（精度）容易欠拟合，精度不高。

样本不均衡问题解决

采样（上采样+下采样）
合成数据（采用已知样本，人为生成更多样本）
样本加权（不同类别分错代价不同）

Sklearn参数

penalty=’l2’, 参数类型：str，可选：‘l1’ or ‘l2’, 默认: ‘l2’。该参数用于确定惩罚项的范数
dual=False, 参数类型：bool,默认：False。双重或原始公式。使用liblinear优化器，双重公式仅实现l2惩罚。
tol=0.0001, 参数类型：float，默认：e-4。停止优化的错误率
C=1.0, 参数类型：float，默认；1。正则化强度的导数，值越小强度越大。
fit_intercept=True, 参数类型：bool，默认：True。确定是否在目标函数中加入偏置。
intercept_scaling=1, 参数类型：float，默认：1。仅在使用“liblinear”且self.fit_intercept设置为True时有用。
class_weight=None, 参数类型：dict，默认：None。根据字典为每一类给予权重，默认都是1.
random_state=None, 参数类型：int，默认：None。在打乱数据时，选用的随机种子。
solver=’warn’, 参数类型：str，可选：{‘newton-cg’, ‘lbfgs’, ‘liblinear’, ‘sag’, ‘saga’}, 默认：liblinear。选用的优化器。
max_iter=100, 参数类型：int，默认：100。迭代次数。multi_class=’warn’, 参数类型：str，可选：{‘ovr’, ‘multinomial’, ‘auto’}，默认：ovr。如果选择的选项是’ovr’，那么二进制问题适合每个标签。对于“多项式”，最小化的损失是整个概率分布中的多项式损失拟合，即使数据是二进制的。当solver 　='liblinear’时，‘multinomial’不可用。如果数据是二进制的，或者如果solver =‘liblinear’，‘auto’选择’ovr’，否则选择’multinomial’。
verbose=0, 参数类型：int，默认：0。对于liblinear和lbfgs求解器，将详细设置为任何正数以表示详细程度。
warm_start=False, 参数类型：bool，默认：False。是否使用之前的优化器继续优化。
n_jobs=None，参数类型：bool，默认：None。是否多线程
参考：
https://blog.csdn.net/qq_27114397/article/details/82947667
https://blog.csdn.net/wsp_1138886114/article/details/80473440