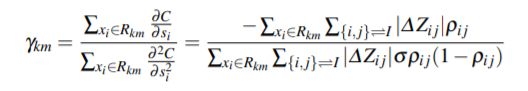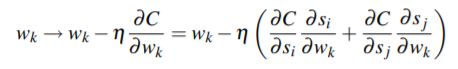关于 LambdaMART 的六个疑惑
目录
一:分类和排序有啥区别?
二:为什么是MART?LambdaMART和MART的区别和关系是啥?
三:学习方式是pair-wise吗?
四:有三个损失函数?
五:直接优化了NDCG吗?
六:预测方式是point-wise?
这里记录的,是针对LambdaMART的一些关键疑惑点的思考。偏基础的介绍可以看一看:
1.Learning To Rank之LambdaMART的前世今生
2.Learning to Rank算法介绍:RankNet,LambdaRank,LambdaMart
3.From RankNet to LambdaRank to LambdaMART: An Overview
4.Deep Learning for Information Retrieval
5.LambdaMART简介——基于Ranklib源码(一 lambda计算)
6.LambdaMART简介——基于Ranklib源码(二 Regression Tree训练)
特别声明:不敢保证结论正确性!可能会持续修正、更新,欢迎留言讨论。
一:分类和排序有啥区别?
刚进入排序领域的人可能会有这样的疑问。
分类学习的对象是类别,排序学习的对象是顺序;二者都不关心模型打分,分类关心的是测试样本被分到了哪一类,排序关心的是目标doc被排在什么位置。
假设眼前有这样一批数据:有800个人,有男有女,有老有少,有高有低,有胖有瘦。有两个任务:1.按性别分成两拨 2.按身高从低到高排成一列。任务1是分类,任务2是排序。你有一个朋友叫钢蛋,现在要加入其中,这就有两个问题:1.钢蛋应该被分在哪一拨,也即判断钢蛋是男的还是女的?2.跟钢蛋身高最接近的10个人是谁?按接近程度从高到底顺序是什么?
对于这两个问题,计算机会怎么做呢?它会观察、学习眼前的800个人的特点。这个过程需要你帮它一把,也就是说你要教一教它。具体的,对于任务1:你让800个人依次走到机器面前给它看一眼,然后告诉它每个人的性别;机器呢,就会观察男人和女人分别由啥特点,比如:女人一般头发长,没有胡子,个子低,胸部凸起,声音偏细,等等。男人则相反。800个人都看了一遍,机器已经基本掌握男人和女人的区别了。这时候钢蛋走过来了,机器一看钢蛋是光头,胡子拉碴,直接就让他左拐归于男性那一堆了,连他胸大不大都不用看了(实际还是看了)。你还有个朋友孟佳觉得好玩也过来看看,机器看着犹豫了一下(实际没有犹豫)把他归于女性了,因为他名字中性,胸肌发达,还留了一头长发。为啥?因为对于机器来说,800个人还不够多,这还没有考虑歪果仁。
对于任务2:你先把这800个人每8个人分一小队,共100个小队;在每一小队里面,找到身高最接近的两个人,让其中一个出来做领队,同时给另外一个人带一个袖章,其它6个人什么都不做;然后,你让每一个小队依次走到机器面前,告诉它那个带袖章的人跟ta的领队身高最接近,同时告诉机器它需要根据与领队身高的接近程度,对这7个人(领队除外)进行降序排序,当然带袖章的人(一开始可能排在一个随机的位置)要排在首位。机器呢,首先看到当前的排队顺序,从前到后高低不平很乱;然后它会认真观察带袖章人和没带袖章的6个人的相似点以及不同的点,想办法把带袖章的人弄到最前面,然后再找从剩下的6个人中找到与带袖章的人身高最接近的,排到前面,队伍就慢慢变整齐了。机器怎么做到的呢?它认为,与带袖章的人性别、胖瘦、籍贯等相近的人高低也相近,这些人排在前面的机会应该大一些。100个小队依次走过,机器终于找到了一定的排队规律,当然只是在学习这100个小队的基础上。现在你的朋友钢蛋来了,机器看了看他的长相,回忆了一下刚看过的800个人,很快挑出了10个人,并且给出了他们从高到低的顺序。你满意的点了点头,说不错。
所以分类和排序有什么区别?只总结一下共同点:你用眼前的800个人教育机器时,机器会学习不同人之间的相似点和不同点,找到一个规律;你在测试机器的时候,机器会观察被测试人的长相,然后放到刚刚学会的规律(分类或者排序)中去给这个人打分,这个分是多少不重要,重要的是是否超过了设定值(分类),或者800人中大家的分值大小关系(排序)。
对应到算法上:800个人是数据集;男、女是标签,带袖章的人也是标签;头发、胡子、声音、胖瘦是特征;规律是学习到的参数;800个人不够多,是数据集太小,模型欠拟合;机器观察、调整,是模型训练;从前到后高低不平,是损失函数在计算损失值。
二:为什么是MART?LambdaMART和MART的区别和关系是啥?
MART是Multiple Additive Regression Tree的简称,更多时候它被叫做GBDT(Gradient Boosting Decision Tree),所以MART是一种经典、强大的机器学习算法,可以用来做分类、回归、排序、推荐任务。LambdaMART之所以闻名,效果好,整体看有两个原因:
首先,是MART本身的优点。作为基于回归树的集成学习方法,MART兼有树模型的强大特征处理能力和集成学习方法的变三个臭皮匠为一个诸葛亮的模型强化能力。回看上面钢蛋的例子,回归树特别擅长观察、学习、总结不同人的身高、体重、头发长短、胖瘦、性别等特征,基于这些特征归纳男女两类人的区别;同时,也可以根据分类结果去反推人物特点。而且,还可以基于对800人的观察学习,给各个特征重要性进行打分排序。特征之间也可以进行组合。总之,这些特征对于树模型来说,可以非常灵活应用和可解释,这对于搜索、推荐等应用场景非常重要。因为这些场景往往需要做大量的特征工程,而且需要很好地进行干预和解释。作为集成学习方法,单棵回归树以标签残差为目标进行拟合训练,MART不断对回归树进行加和、算残差。这样做有这样的好处,即前面拟合的回归树会更多关注对多数样本有区分度的特征,后面拟合的树会更加关注残差仍然较大的少数训练数据。因此在训练MART模型时,MART算法会优先考虑对大部分样本区分度大的特征,然后再针对剩下的少数样本有区分度的特征,理论上更合理。这种方式与随机森林等集成方法有明显的区别,kaggle等竞赛榜单也用事实证明了MART的实力。
其次,是Lambda梯度嵌入MART算法非常合理、自然。MART的内在设定是支持一般损失函数,因此使用损失函数对当前模型打分函数的梯度作为每一个训练样本的近似残差
对每一个样本,F(m-1) 和 y(i) 是已知的,因此可以算出其近似残差,作为后面一颗回归树的拟合对象。当损失函数是MSE时,计算出的结果就是真实的残差
再来看pair对
也是损失函数对打分函数的梯度,连形式都非常像,只是乘了一个排序指标数值。给定一个样本(doc pair),模型打分s(i)和s(j)是已知的,排序指标数值也可以根据打分计算出来,因此pair对
所以本质上,LambdaMART是MART为了解决排序任务而对自身的一种调整。这种调整完全没有影响到MART的整体算法架构,只是改变了残差计算方式,也即回归树的拟合目标,改成了lambda。Lambda的计算对MART来说,是一个非常独立、插件化的过程,与训练集中的doc顺序、打分、标签有关。MART通过预测打分 -> doc排序 -> 计算lambda -> 拟合新回归树 -> 更新MART模型 -> 预测打分 ... 循环与lambda交互,直到回归树数量达到预先设定的值。
三:学习方式是pair-wise吗?
以pair-wise为主,兼有list-wise性质。
从公式 (3) lambda的定义来看,LambdaMART引入了NDCG评价指标。我们来看NDCG的定义
其中T指top T,i是排序位置,l(i)是标签。可见,NDCG评价的对象是doc list,因此LambdaMART因为引入NDCG而具有doc list性质。但整体上看,LambdaMART主要的考察对象仍然是doc pair,即使|![]() NDCG|也是交换两个doc的位置产生的,所以属于pair-wise。
NDCG|也是交换两个doc的位置产生的,所以属于pair-wise。
四:有三个损失函数?
标准的MART模型有两个损失函数。
MART损失函数
推导过程省略,直接给出结论公式
对其求一阶导,得到回归树要拟合的近似残差,公式(1)和公式(2)已经有相关说明。建立回归树的过程中,MART算法保证损失函数在每个叶子节点获得最小值,进而使总的损失函数最小化。目标是
即搜索到最优的![]() 使得损失函数在当前叶子节点具有最小值,具体办法是牛顿法
使得损失函数在当前叶子节点具有最小值,具体办法是牛顿法
从最后结果看,叶子节点返回值等于公式(6)的一阶导与二阶段的比值,即
回归树损失函数
一般采用均方误差,即MSE。也可以采用基尼指数、信息增益等方法。单个样本的函数表达式见公式(2)。回归树损失函数用于拟合单棵回归树,具体是评价划分出的数据集质量。理想的,希望落在同一个数据子集中的样本具有同样的标签(从信息论角度讲,此时信息量最小,纯度最高),即Fn=y,这样损失函数C就是0了。
两个损失函数是什么关系呢?如前述,回归树的损失函数在构建回归树子模型时发挥作用,目标是使得划分开的两个数据子集信息量最小;相比回归树损失函数,MART的损失函数是全局性的,作用于每个叶子节点,通过牛顿迭代的方式找到当前叶子节点区域中使得损失函数最小的lambda值,即叶子节点返回值。该值会作为落在当前叶子节点中所有样本的残差,成为下一课回归树拟合的目标。
LambdaMART呢?LambdaMART引入了lambda,lambda定义中暗含了一个损失函数,再考虑MART的损失函数,因此有人疑惑:难道LambdaMART有三个损失函数?不是,LambdaMART中暗含的这个损失函数扮演了MART损失函数的角色。具体的,由公式(3)反推,得到
因此有一阶导g', 即Lambda
二阶导g''
最后,得到叶子节点近似残差
可以看到与公式(9)形式一致。LambdaMART中回归树的损失函数与MART没有区别。
所以答案是,LambdaMART有两个损失函数,回归树损失函数与MART一样,全局损失函数设计思路大不相同。
五:直接优化了NDCG吗?
答案是没有定论。
开篇提及的文献3和文献4都是比较权威的资料,文献4只给出了结论,没有进一步的解释
文献3给出了相反的观点
同时作者用引用同行论文的方式给出了解释
先定义了NDCG和W的比值公式,用于观察NDCG如何随着M变化;然后假定NDCG均值M是模型参数W(假设固定成一个)的函数,w*是最优值,反推M在W=w*时取得最大值。后面是证明这个推论,考虑到w*可能是鞍点,因此用蒙特卡洛算法去试探,最后给出了最小试探次数的表达式
就结束了。没有看太懂。
直觉上,我个人倾向于支持文献3的观点,即LambdaMART直接优化了NDCG(在这个问题上,LambdaMART与LambdaNet等效)。从整体模型角度看公式(3),S函数是最终的训练结果,s(i),s(j),|![]() NDCG|的直接作用结果都是S函数;|
NDCG|的直接作用结果都是S函数;|![]() NDCG|的计算过程是,先根据S函数的预测打分对doc进行排序,然后基于doc位置和标签(即lambda,是已知的数值)计算一个doc pair交换位置后的NDCG差值。因此,|
NDCG|的计算过程是,先根据S函数的预测打分对doc进行排序,然后基于doc位置和标签(即lambda,是已知的数值)计算一个doc pair交换位置后的NDCG差值。因此,|![]() NDCG|的计算过程参考了S函数的预测结果,从这个角度看,|
NDCG|的计算过程参考了S函数的预测结果,从这个角度看,|![]() NDCG|在公式(3)中发挥的作用与s(i),s(j)是等效的。
NDCG|在公式(3)中发挥的作用与s(i),s(j)是等效的。
六:预测方式是point-wise?
有人会有这样的疑惑:LambdaMART训练的时候输入是doc pair,训练的核心是两个doc的相对位置,但测试的时候输入是单个doc(即query),给出的结果是每一棵树上某一个叶子节点返回值的加权和,总感觉哪里不对?是的,看起来跟基本分类、回归任务非常不同。先说结论,LambdaMART的预测过程与MART没有什么不同,因为LambdaMART的整体算法框架与MART一样,只是计算残差的“插件”变了,考虑了样本之间的相关度、位置关系等信息。据我所知,xxx-wise是针对排序算法的一种训练策略的归类描述,预测过程没有这种说法。
对于这个问题,RankNet,LambdaNet,LambdaMART等效,先看比较好理解的RankNet。
RankNet
先列公式
公式(14)是i比j更相关的概率预测值,公式(15)是i比j更相关的概率实际值,其中S(ij)的取值是 -> 1,i 比 j 更相关;1/2,同样相关;0,j 比i更相关。损失函数是
把(14)和(15)带入(16),然后对s(i)和s(j)求导,利用梯度下降算法不断更新s(i),s(j),达到最小化损失函数C的目标,这就是RankNet的训练过程。RankNet背后的算法是神经网络,所以学习出来的函数S其参数是连接神经元的权重。
普通的神经网络Net,其经过softmax操作之后输出的是一个概率向量,其中的每一个元素是表示属于某一类别的概率值。基于此与真实标签比较,进而产生损失,表现在损失函数的数值上。RankNet的损失也是概率的差值,只是概率的意义是一个样本比另一个样本更相关的程度。因此从模型训练上讲,普通的Net与RankNet只是训练策略上的差异,其输出的分类概率的本质是一样的。整体看,普通的分类、回归模型,其测试过程和训练过程是一致的;而类似pair-wise这样的排序模型,其训练过程是在测试过程的基础上(模型的打分或输出的概率值)多加了一些策略,比如样本位置信息、样本之间相关程度等,以便达到排序的目的。
具体看分类(或者回归)模型的训练过程和测试过程。在训练分类模型的过程中,借助于预测类别概率(也可认为是打分)与实际类别的差别作用于最小化损失函数来学习类别之间的特征区别;在预测时模型时,比较测试样本的特征和自己学到的类别之间的特征区别(参数)给出各个类别的打分,最终把测试样本归于打分最高的类别。可以看出,分类模型训练和测试过程是一致的。
再看RankNet的训练过程和测试过程。已经定义了损失函数(16),因此计算梯度
可以看出,虽然损失函数中直接定义的变量是doc pair
既然RankNet的训练过程和普通分类任务的训练过程本质上一致的,都是学习出模型S参数(函数),那么RankNet的预测过程就跟它的训练过程也是一致的,因为RankNet的预测过程我们非常熟悉,跟普通分类很相似。普通分类的预测过程是,给模型一个输入,模型输出一个打分(类别概率),根据打分的高低判断出所属类别;RankNet呢,也是给S函数输入一个doc,得到一个打分,最后根据打分对doc排序。再来看
LambdaRank
LambdaRank与RankNet的区别在于计算梯度的方式不同。先列公式
其中的关键是公式(21)。这种方法只考虑了doc i 和doc j 之间的相关程度,没有考虑到他们在整体doc list的位置关系,因此与query相关度非常高的doc i 的位置有可能被往后排(因为损失函数可能变小)。为了解决这个问题,智慧的同行前辈重新定义了公式(21),这就是Lambda
公式(22)从形式上没有变,只是Lambda的值变了。需要特别说明的是,LambdaRank的损失函数C不是公式(16)中的C,这里的C是根据公式(3)反推出来的,即公式(10)中的C,而且LambdaRank的优化目标是最大化C。不过显然,这不影响结论,即LambdaRank的训练过程和测试过程本质上也是一致的。因为梯度计算方式不同,影响的只是更新模型参数W的过程,最终的结果还是以W为参数的模型S。最后看LambdaMART。
LambdaMART
LambdaMART的训练和预测过程当然也是一致的。
LambdaMART和LambdaRank的区别就跟它们名称的区别一样,是MART和Rank的区别,很多对LambdaMART的疑惑,其实源自对MART的疑惑。对MART本身的疑惑,加上引入Lambda后的疑惑使人更加的疑惑。
LambdaMART的训练流程是:预测打分 -> doc排序 -> 计算lambda -> 拟合新回归树 -> 更新MART模型 -> 预测打分 ... 循环与lambda交互,直到回归树数量达到预先设定的值。doc排序是计算lambda 的一部分,二者合起来与MART计算残差的方式相对应,其本质是MART为了实现排序任务而对残差计算方式做的改进,这就是LambdaMART和MART的区别。所以如果MART的训练过程和预测过程是一致,那么LambdaMART的训练和预测过程也是一致的,就跟Net、RankNet、LambdaRank之间的区别一样。
MART本身这里不赘述,需要注意的是MART损失函数,以及叶子节点上的返回值计算。损失函数前面介绍过了,这里讨论一下叶子节点的返回值。如果回归树的损失函数是MSE,则节点会有两种值:
1.落在本节点(可能是父节点,也可能是叶子节点)上所有样本标签残差的平均值;
2.根据牛顿法计算出来的最优值(叶子节点)
平均值用来寻找最佳划分点以便拟合回归树,最优值则是在叶子节点上计算出的返回值,即公式(9)的计算结果。
文献3指出,g'是lambda梯度,1/g''是梯度下降的step size,我没发现这样的解释有什么意义。
输入一个测试样本,该样本会依次落入MART模型每棵树的某个叶子节点,这些回归树子模型依次返回对应叶子节点上的值,各自乘以学习率(正则系数)然后加起来,结果就是MART模型对该样本的打分。上述讨论把MART换成LambdaMART同样适用。