网络流入门 -- 2020.7.20 - 2020.7.25
网络流
Dinic 解最大流
还真是,这个算法不用太懂…直接add然后run就行,难点在建图,奥还有读题…
板子放最后
POJ 1149 PIGS
多源多汇 , 因为猪在猪圈里可以随意更改,所以对每一个猪圈,有一个人拿了出来之后,能转交给其他所有有这个钥匙的人任意数量的猪,最后所有人连上汇点,权重为这个人的需求即可
HDU 3416 Marriage Match IV (Dijkstra+最大流)
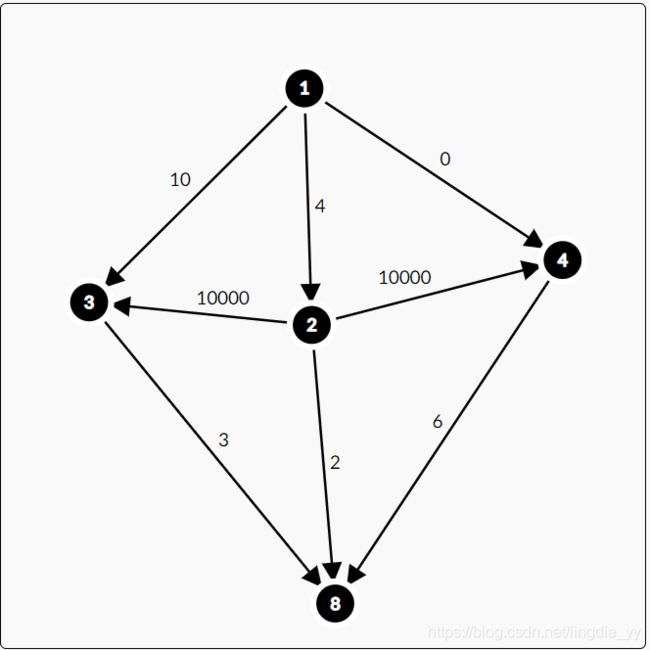
问题是求 从S到T的不经过同一条边的最短路数量,可以分成下面几个小问题
- 如何判断边是否在最短路径上?
最短路径满足条件是对现在的所有 [u->v] 边 都有: d[u] + cost <= d[v]
明显当 d[u] + cost == d[v] 时, [u->v] 的这条边在最短路径上- 如何计数?
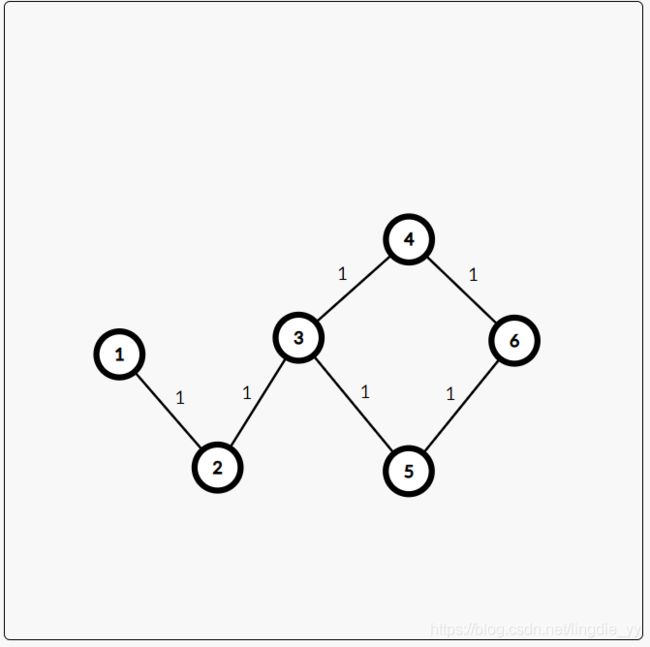
冷静分析一波 , 假设现在就只有两个点 要计算 a->b 的 不经过同一个边最短路数量,那就是要计算 a->b 的边中有多少个和最小边相同的边数.可以发现,最短路上的权值不影响最后的计数了. 那么推展到n个结点 ,答案就是以最短路径建权值都是1的图,从 S->T的 最大流.
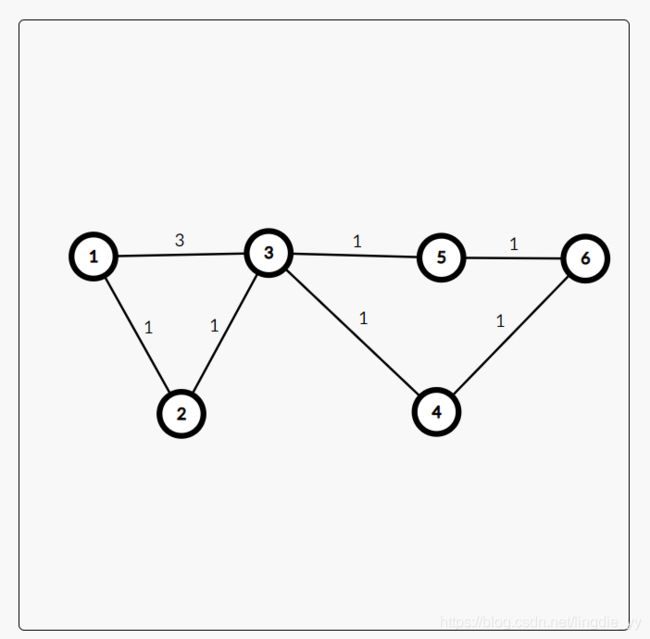
- 扩展 :当题目要求为不经过相同结点时怎么计数?
问题转化为结点容量为1 ,从S->T的最大流 ,拆点, 将路径上的每个点拆成 i 和 i+n 加权为1的边即可.
Dinic 解二分图匹配
HDU - 4292 Food
因为每个人只能满意一次,要把人拆点,从源点到人的边权为食物,从人到汇点的边权为饮料
//vector存边,queue操作较慢
const ll inf = 0x3f3f3f3f;
const ll maxn = 1e5 + 7;
struct Dinic
{
struct edge
{
int to, cap, rev;
edge(int a, int b, int c)
{
to = a, cap = b, rev = c;
}
};
vector<edge> G[maxn];
int level[maxn];
int iter[maxn];
void init(int n)
{
memset(level, 0, sizeof level);
memset(iter, 0, sizeof iter);
for (int i = 0; i <= n; i++)
G[i].clear();
}
void add(int from, int to, int cap)
{
G[from].push_back(edge(to, cap, G[to].size()));
G[to].push_back(edge(from, 0, G[from].size() - 1));
}
void bfs(int s)
{
memset(level, -1, sizeof level);
queue<int> que;
level[s] = 0;
que.push(s);
while (que.size())
{
int v = que.front();
que.pop();
for (int i = 0; i < G[v].size(); i++)
{
edge &e = G[v][i];
if (e.cap > 0 && level[e.to] < 0)
level[e.to] = level[v] + 1, que.push(e.to);
}
}
}
int dfs(int v, int t, int f)
{
if (v == t)
return f;
for (int &i = iter[v]; i < G[v].size(); i++)
{
edge &e = G[v][i];
if (e.cap > 0 && level[v] < level[e.to])
{
int d = dfs(e.to, t, min(f, e.cap));
if (d > 0)
{
e.cap -= d, G[e.to][e.rev].cap += d;
return d;
}
}
}
return 0;
}
int run(int s, int t)
{
int flow = 0;
while (1)
{
bfs(s);
if (level[t] < 0)
return flow;
memset(iter, 0, sizeof iter);
int f;
while ((f = dfs(s, t, inf)) > 0)
flow += f;
}
}
} F;
//前向星,快的起飞
const ll inf = 0x3f3f3f3f;
const ll maxn = 1e5 + 7;
const int MX = 1e3;
const int MS = 4e5 + 5;
const int INF = 0x3f3f3f3f;
template <class T>
struct Max_Flow
{
int n;
int Q[MX], sign;
int head[MX], level[MX], cur[MX], pre[MX];
int nxt[MS], pnt[MS], E;
T cap[MS];
void init(int n)
{
E = 0;
this->n = n + 1;
fill(head, head + this->n, -1);
}
void add(int from, int to, T c, T rw = 0)
{
// cout << from << " " << to << " " << c << endl;
pnt[E] = to;
cap[E] = c;
nxt[E] = head[from];
head[from] = E++;
pnt[E] = from;
cap[E] = rw;
nxt[E] = head[to];
head[to] = E++;
}
bool BFS(int s, int t)
{
sign = t;
std::fill(level, level + n, -1);
int *front = Q, *tail = Q;
*tail++ = t;
level[t] = 0;
while (front < tail && level[s] == -1)
{
int u = *front++;
for (int e = head[u]; e != -1; e = nxt[e])
{
if (cap[e ^ 1] > 0 && level[pnt[e]] < 0)
{
level[pnt[e]] = level[u] + 1;
*tail++ = pnt[e];
}
}
}
return level[s] != -1;
}
void Push(int t, T &flow)
{
T mi = INF;
int p = pre[t];
for (int p = pre[t]; p != -1; p = pre[pnt[p ^ 1]])
{
mi = std::min(mi, cap[p]);
}
for (int p = pre[t]; p != -1; p = pre[pnt[p ^ 1]])
{
cap[p] -= mi;
if (!cap[p])
{
sign = pnt[p ^ 1];
}
cap[p ^ 1] += mi;
}
flow += mi;
}
void DFS(int u, int t, T &flow)
{
if (u == t)
{
Push(t, flow);
return;
}
for (int &e = cur[u]; e != -1; e = nxt[e])
{
if (cap[e] > 0 && level[u] - 1 == level[pnt[e]])
{
pre[pnt[e]] = e;
DFS(pnt[e], t, flow);
if (level[sign] > level[u])
{
return;
}
sign = t;
}
}
}
T Dinic(int s, int t)
{
pre[s] = -1;
T flow = 0;
while (BFS(s, t))
{
std::copy(head, head + n, cur);
DFS(s, t, flow);
}
return flow;
}
};
Max_Flow<int> F;