UUUUh
UUUUh

2018年ICPC徐州现场赛M - Rikka with Illuminations（计算几何+贪心）

菜鸡终于写出来了

题目链接：https://codeforces.com/gym/102012/problem/M

题意：按逆时针方向给你n个凸多边形的顶点，在凸多边形的外侧给你m个点光源，用最小的点光源照射到所有的边，输出光源序号。

题解：每个点光源照射的边的一定是连续的，那么就可以转化为区间覆盖问题，先处理每个点光源的最大覆盖区间（可以用叉积解决），然后贪心做就行啦。

时间复杂度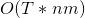O(T*nm)

ps：这个题竟然卡输出格式。

另附代码：

# define _CRT_SECURE_NO_WARNINGS
#pragma GCC optimize(2)
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#define Pair pair
//#define int long long
#define fir first
#define sec second

namespace fastIO {
#define BUF_SIZE 100000
#define OUT_SIZE 100000
  //fread->read
  bool IOerror = 0;
  //inline char nc(){char ch=getchar();if(ch==-1)IOerror=1;return ch;}
  inline char nc() {
    static char buf[BUF_SIZE], * p1 = buf + BUF_SIZE, * pend = buf + BUF_SIZE;
    if (p1 == pend) {
      p1 = buf; pend = buf + fread(buf, 1, BUF_SIZE, stdin);
      if (pend == p1) { IOerror = 1; return -1; }
    }
    return *p1++;
  }
  inline bool blank(char ch) { return ch == ' ' || ch == '\n' || ch == '\r' || ch == '\t'; }
  template inline bool read(T& x) {
    bool sign = 0; char ch = nc(); x = 0;
    for (; blank(ch); ch = nc());
    if (IOerror)return false;
    if (ch == '-')sign = 1, ch = nc();
    for (; ch >= '0' && ch <= '9'; ch = nc())x = x * 10 + ch - '0';
    if (sign)x = -x;
    return true;
  }
  inline bool read(double& x) {
    bool sign = 0; char ch = nc(); x = 0;
    for (; blank(ch); ch = nc());
    if (IOerror)return false;
    if (ch == '-')sign = 1, ch = nc();
    for (; ch >= '0' && ch <= '9'; ch = nc())x = x * 10 + ch - '0';
    if (ch == '.') { double tmp = 1; ch = nc(); for (; ch >= '0' && ch <= '9'; ch = nc())tmp /= 10.0, x += tmp * (ch - '0'); }
    if (sign)x = -x; return true;
  }
  inline bool read(char* s) {
    char ch = nc();
    for (; blank(ch); ch = nc());
    if (IOerror)return false;
    for (; !blank(ch) && !IOerror; ch = nc())* s++ = ch;
    *s = 0;
    return true;
  }
  inline bool read(char& c) {
    for (c = nc(); blank(c); c = nc());
    if (IOerror) { c = -1; return false; }
    return true;
  }
  templatebool read(T& h, U& ... t) { return read(h) && read(t...); }
#undef OUT_SIZE
#undef BUF_SIZE
};
using namespace fastIO;
using namespace std;


/*---------------------------------------------------------------------------------------------------------------------------*/
const double eps = 1e-10;
struct Point { double x, y; Point(double x = 0, double y = 0) :x(x), y(y) {} };
typedef Point Vector;
Vector operator + (Vector A, Vector B) { return Vector(A.x + B.x, A.y + B.y); }
Vector operator - (Point A, Point B) { return Vector(A.x - B.x, A.y - B.y); }
Vector operator * (Vector A, double p) { return Vector(A.x * p, A.y * p); }
Vector operator / (Vector A, double p) { return Vector(A.x / p, A.y / p); }
bool operator < (const Point& A, const Point& B) { return A.x < B.x || (A.x == B.x && A.y < B.y); }
int dcmp(double x) { if (fabs(x) < eps)return 0; else return x < 0 ? -1 : 1; }
bool operator == (const Point& A, const Point& B) { return dcmp(A.x - B.x) == 0 && dcmp(A.y - B.y) == 0; }
double Dot(Vector A, Vector B) { return A.x * B.x + A.y * B.y; }
double Length(Vector A) { return sqrt(Dot(A, A)); }
double Dist2(const Point& A, const Point& B) { return (A.x - B.x) * (A.x - B.x) + (A.y - B.y) * (A.y - B.y); }
double Dist(const Point& A, const Point& B) { return sqrt((A.x - B.x) * (A.x - B.x) + (A.y - B.y) * (A.y - B.y)); }
double Angle(Vector A, Vector B) { return acos(Dot(A, B) / Length(A) / Length(B)); }
double Cross(Vector A, Vector B) { return A.x * B.y - A.y * B.x; }
double Area2(Point A, Point B, Point C) { return Cross(B - A, C - A); }
double DistanceToLine(Point P, Point A, Point B) { Vector v1 = B - A, v2 = P - A; return fabs(Cross(v1, v2)) / Length(v1); }
Vector Normal(Vector A) { double L = Length(A); return Vector(-A.y / L, A.x / L); }
Vector Rotate(Vector A, double rad) { return Vector(A.x * cos(rad) - A.y * sin(rad), A.x * sin(rad) + A.y * cos(rad)); }
Point GetLineIntersection(Point P, Vector v, Point Q, Vector w) { Vector u = P - Q; double t = Cross(w, u) / Cross(v, w); return P + v * t; }
double PolygonArea(vectorp) {//duo area
  double area = 0;
  int n = p.size();
  for (int i = 1; i < n - 1; i++)area += Cross(p[i] - p[0], p[i + 1] - p[0]);

  return area / 2;
}
double torad(double deg) { return deg / 180 * acos(-1); }
vector ConvexHull(vector& p) {
  sort(p.begin(), p.end());
  p.erase(unique(p.begin(), p.end()), p.end());
  int n = p.size();
  int m = 0;
  vector ch(n + 1);
  for (int i = 0; i < n; i++) { while (m > 1 && Cross(ch[m - 1] - ch[m - 2], p[i] - ch[m - 2]) <= 0)m--; ch[m++] = p[i]; }
  int k = m;
  for (int i = n - 2; i >= 0; i--) { while (m > k && Cross(ch[m - 1] - ch[m - 2], p[i] - ch[m - 2]) <= 0)m--; ch[m++] = p[i]; }
  if (n > 1)m--;
  ch.resize(m);
  return ch;
}
double diameter2(vector& points) {
  vectorp = ConvexHull(points);
  int n = p.size();
  if (n == 1) return 0;
  if (n == 2) return Dist2(p[0], p[1]);
  //p.push_back(p[0]); // 免得取模
  double ans = 0;
  for (int u = 0, v = 1; u < n; u++) {
    for (;;) {
      //Cross(p[u+1]-p[u],p[v+1]-p[v])<=0时停止旋转
      int diff = Cross(p[u + 1] - p[u], p[v + 1] - p[v]);
      if (diff <= 0) {
        ans = max(ans, Dist2(p[u], p[v])); // u和v是对踵点
        if (diff == 0) ans = max(ans, Dist2(p[u], p[v + 1])); // diff == 0时u和v+1也是对踵点
        break;
      }
      v = (v + 1) % n;
    }
  }
  return ans;
}
Point PolygonCenter(vectorp) {
  Point ans(0, 0);
  int n = p.size();
  if (PolygonArea(p) == 0)return ans;
  for (int i = 0; i < n; i++) {
    ans = ans + (p[i] + p[(i + 1) % n]) * Cross(p[i], p[(i + 1) % n]);
  }
  return ans / PolygonArea(p) / 6.0;
}

/*---------------------------------------------------------------------------------------------------------------------------*/
struct Line {
  Point P;
  Vector v;
  double ang;
  Line() {}
  Line(Point P, Vector v) :P(P), v(v) { ang = atan2(v.y, v.x); }
  bool operator < (const Line& L)const {
    return ang < L.ang;
  }
};
Point GetLineIntersection(const Line& a, const Line& b) {
  Vector u = a.P - b.P;
  double t = Cross(b.v, u) / Cross(a.v, b.v);
  return a.P + a.v * t;
}
bool OnLeft(Line L, Point p) { return Cross(L.v, p - L.P) > 0; }
vectorHalfplaneIntersection(vectorL) {
  int n = L.size();
  sort(L.begin(), L.end());
  int first, last;
  vector p(n);
  vector q(n);
  vector ans;
  q[first = last = 0] = L[0];
  for (int i = 1; i < n; i++) {
    while (first < last && !OnLeft(L[i], p[last - 1])) last--;
    while (first < last && !OnLeft(L[i], p[first]))first++;
    q[++last] = L[i];
    if (fabs(Cross(q[last].v, q[last - 1].v)) < eps) {
      last--;
      if (OnLeft(q[last], L[i].P))q[last] = L[i];
    }
    if (first < last)p[last - 1] = GetLineIntersection(q[last - 1], q[last]);
  }
  while (first < last && !OnLeft(q[first], p[last - 1]))last--;//删除无用平面
  if (last - first <= 1)return ans;
  p[last] = GetLineIntersection(q[last], q[first]);//计算首尾两个半平面的交点
  //从deque复制到输出中
  for (int i = first; i <= last; i++)ans.push_back(p[i]);
  return ans;
}
bool OnSegment(const Point& p, const Point& a1, const Point& a2) {
  return dcmp(Cross(a1 - p, a2 - p)) == 0 && dcmp(Dot(a1 - p, a2 - p)) < 0;
}
bool SegmentProperIntersection(const Point& a1, const Point& a2, const Point& b1, const Point& b2) {
  double c1 = Cross(a2 - a1, b1 - a1), c2 = Cross(a2 - a1, b2 - a1),
    c3 = Cross(b2 - b1, a1 - b1), c4 = Cross(b2 - b1, a2 - b1);
  return dcmp(c1) * dcmp(c2) < 0 && dcmp(c3) * dcmp(c4) < 0;
}
int IsPointInPolygon(const Point& p, const vector& poly) {
  int wn = 0;
  int n = poly.size();
  for (int i = 0; i < n; i++) {
    const Point& p1 = poly[i];
    const Point& p2 = poly[(i + 1) % n];

    if (p1 == p || p2 == p || OnSegment(p, p1, p2)) return -1; // 在边界上
    //if (dcmp(dists(p, p1, p2)) == 0) return 0;

    int k = dcmp(Cross(p2 - p1, p - p1));
    int d1 = dcmp(p1.y - p.y);
    int d2 = dcmp(p2.y - p.y);
    if (k > 0 && d1 <= 0 && d2 > 0) wn++;
    if (k < 0 && d2 <= 0 && d1 > 0) wn--;
  }
  if (wn != 0) return 1; // 内部
  return 0; // 外部
}
bool ConvexPolygonDisjoint(const vector ch1, const vector ch2) {
  int c1 = ch1.size();
  int c2 = ch2.size();
  cout << "c1 " << c1 << " " << "c2 " << c2 << endl;
  for (int i = 0; i < c1; i++)
    if (IsPointInPolygon(ch1[i], ch2) != 0) return false; // 内部或边界上
  for (int i = 0; i < c2; i++)
    if (IsPointInPolygon(ch2[i], ch1) != 0) return false; // 内部或边界上
  for (int i = 0; i < c1; i++)
    for (int j = 0; j < c2; j++)
      if (SegmentProperIntersection(ch1[i], ch1[(i + 1) % c1], ch2[j], ch2[(j + 1) % c2])) return false;
  return true;
}
/*---------------------------------------------------------------------------------------------------------------------------*/
struct Circle {
  Point c;
  double r;
  Circle(Point c, double r) :c(c), r(r) {}
  Point point(double a) {
    return Point(c.x + cos(a) * r, c.y + sin(a) * r);
  }
};
double angle(Vector v) { return atan2(v.y, v.x); }
int getCircleCircleIntersection(Circle C1, Circle C2, vector& sol) {
  double d = Length(C1.c - C2.c);
  if (dcmp(d) == 0) {   //首先圆心要重合
    if (dcmp(C1.r - C2.r) == 0) return -1; //其次半径要相同，然后就可以推出两圆重合
    return 0;
  }
  if (dcmp(C1.r + C2.r - d) < 0) return 0; //相离没交点
  if (dcmp(fabs(C1.r - C2.r) - d) > 0) return 0; //圆在圆中，没有交点
  double a = angle(C2.c - C1.c); //向量C1C2的极角
  double da = acos((C1.r * C1.r + d * d - C2.r * C2.r) / (2 * C1.r * d)); //C1C2到C1P1的角
  Point p1 = C1.point(a - da), p2 = C1.point(a + da);
  sol.push_back(p1);
  if (p1 == p2) return 1; //相切
  sol.push_back(p2);
  return 2; //相交
}
bool isInCircle(Point p, Circle cir) {
  return dcmp(Dist2(p, cir.c) - cir.r * cir.r) < 0;
}
bool check(vectorp, vectorcir) {
  if (p.empty()) return true;
  for (int i = 0; i < p.size(); i++) {
    bool ok = true;
    Point tp = Point(-p[i].x, -p[i].y);
    for (int j = 1; j < cir.size(); j++)
      if (isInCircle(tp, cir[j])) { ok = false; break; }
    if (ok)return true;
  }
  return false;
}

/*---------------------------------------------------------------------------------------------------------------------------*/

const int N = 2e5 + 5;
const double pi = acos(-1.0);
typedef long long ll;
//const int mod = 998244353;
const int mod = 1e9 + 7;
#define inf 0x3f3f3f3f
struct ship {
  double x, y, step;
  ship(double x, double y, double step) :x(x), y(y), step(step) {}
};
struct thing {
  int num, period, time;
  bool operator < (const thing& y)const {
    return y.time < time || (y.time == time && y.num < num);
  }
  thing() {}
  thing(int num, int period, int time) :num(num), period(period), time(time) {}
};
int dx[8] = { 0, 0, 1,-1, 1, 1,-1,-1 };
int dy[8] = { 1,-1, 0, 0, 1,-1, 1,-1 };


signed main() {
  //freopen("Data.txt", "r", stdin);
  int t;
  scanf("%d", &t);
  while (t--) {
    int n, m;
    scanf("%d%d", &n, &m);
    vectorpoly, light;
    for (int i = 0; i < n; i++) {
      double x, y;
      scanf("%lf%lf", &x, &y);
      poly.push_back(Point(x, y));
    }

    for (int i = 0; i < m; i++) {
      double x, y;
      scanf("%lf%lf", &x, &y);
      light.push_back(Point(x, y));
    }
    vectorto(n, 0), id(n, 0);
    for (int i = 0; i < m; i++) {
      int l = 0, r = 0;
      for (int j = 1; j < n; j++) {
        if (Cross(poly[j] - light[i], poly[l] - light[i]) < 0) l = j;
        if (Cross(poly[j] - light[i], poly[r] - light[i]) > 0) r = j;
      }
      for (int j = l; j != r; j = (j + 1) % n) {
        if (to[j] < (r - j + n) % n) {
          to[j] = (r - j + n) % n;
          id[j] = i + 1;
        }
      }
    }

    bool ok = 0;
    for (int i = 0; i < n; i++)
      if (to[i] == 0) { ok = 1; break; }
    if (ok) { printf("-1\n"); continue; }
    int mn = m, base;
    for (int i = 0; i < n; i++) {
      int num = 0;
      int j = i;
      while (j < i + n) {
        j += to[j % n];
        num++;
      }
      if (num < mn) {
        mn = num;
        base = i;
      }
    }
    printf("%d\n", mn);
    for (int i = 0; i < mn; i++) {
      printf("%d%c", id[base], i < mn - 1 ? ' ' : '\n');
      base = (base + to[base]) % n;
    }
  }
  return 0;
}

/*
1
3 3
0 0
1 0
0 1
-1 -1
3 -1
-1 3
*/

 

你可能感兴趣的:(0x07贪心,0x73二维凸包)

  • ID290－ID293 《初刻拍案惊奇》主人公人物定位分布:原文 小赞的坚果喵
    卷十五卫朝奉狠心盘贵产陈秀才巧计赚原房诗曰:人生碌碌饮贪泉，不畏官司不顾天。何必广斋多忏悔？让人一着最为先。这一首诗，单说世上人贪心起处，便是十万个金刚也降不住；明明的刑宪陈设在前，也顾不的。子列子有云：“不见人，徒见金。”盖谓当这点念头一发，精神命脉，多注在这一件事上，那管你行得也行不得？话说杭州府有一贾秀才，名实，家私巨万，心灵机巧，豪侠好义，专好结识那一班有义气的朋友。若是朋友中有那未娶妻的
  • LeetCode 面试经典150题 55.跳跃游戏 hn小菜鸡 算法刷题-数组leetcode面试游戏
    题目：给你一个非负整数数组nums，你最初位于数组的第一个下标。数组中的每个元素代表你在该位置可以跳跃的最大长度。判断你是否能够到达最后一个下标，如果可以，返回true；否则，返回false。思路：贪心代码：classSolution{publicbooleancanJump(int[]nums){intn=nums.length;intrightMost=0;for(inti=0;i=n-1)r
  • 写给小白——Android动画之位移动画（移动动画） justCode_
    前面讲了，透明动画和缩放动画，今天单独讲讲位移动画。因为位移动画，真的是相对而言，变化最多，也最难（当然，也不难，会就不难）首先，我喜欢先讲方法和结果。然后，再讲原理。移动动画的代码，就这么多，这里的代码，几乎是位移动画的全部了。这里，我先不讲每个参数是什么。我准备在文末解释。我红框选中的地方，是我今天讲的重点。首先，我们讲一个东西，我今天讲的是平面位移（也叫二维位移）。当然，有三维（俗称3D）的
  • LeetCode分发糖果(贪心思路分析) 酸奶代码 贪心算法leetcode算法贪心算法c++
    题目描述贪心思路思路及解法我们可以将「相邻的孩子中，评分高的孩子必须获得更多的糖果」这句话拆分为两个规则，分别处理。左规则：当ratings[i−1]ratings[i+1]时，i号学生的糖果数量将比i+1号孩子的糖果数量多。我们遍历该数组两次，处理出每一个学生分别满足左规则或右规则时，最少需要被分得的糖果数量。每个人最终分得的糖果数量即为这两个数量的最大值。具体地，以左规则为例：我们从左到右遍历
  • vue-element根据后端返回的值，在表格内生成二维码并且下载 爬坑的小白 vue.jsjavascriptchrome
    1:安装qrcodenpmiqrcode2:引入qrcodeimportQRCodefrom'qrcode'3:页面下载4:方法//封装方法生产二维码asyncgetCode(data){console.log(data,';;;')try{constdataSting=data.toString()constqrCodeData=awaitQRCode.toDataURL(dataSting)r
  • NoSQL（非关系型数据库）之Redis 花狮66 nosqlredis数据库
    目录一、关系型数据库与非关系型数据库1.1关系型数据库1.2非关系型数据库1.3区别1.3.1数据存储方式不同1.3.2扩展方式不同1.4非关系型数据库产生背景二、Redis简介2.1Redis概述2.2Redis优点2.3Redis为什么这么快？总结一数据流向二各自特点一、关系型数据库与非关系型数据库1.1关系型数据库关系型数据库是一个结构化的数据库，创建在关系模型(二维表格模型)基础上，一般面
  • 2-85 基于matlab的FrFT下时变幅度LFM信号参数估计 'Matlab学习与应用 matlab工程应用matlab人工智能算法一维插值峰值搜索方式二维峰值搜索算法下时变幅度LFM信号参数估计FrFT
    基于matlab的FrFT下时变幅度LFM信号参数估计，输入高斯白噪声LFM信号(信噪比可定义)，采用二维峰值搜索算法及一维插值峰值搜索方式提供计算速度，输出LFM信号参数估计结果。程序已调通，可直接运行。2-85一维插值峰值搜索方式-小红书(xiaohongshu.com)
  • 数据库的介绍：关系型数据库和非关系型数据库究竟是什么？ 一名在八月份找工作的测试员 数据库nosql
    1.数据库是什么？数据库（DB）是按照一定数据结构存储数据的仓库2.数据库管理系统是什么？数据库管理系统（DBMS）是操纵和管理数据库的一套软件。市面上主流的有Mysql/oracle/sqlserver3.数据库管理系统又可以分为哪些类型？数据库管理系统可以分为：关系型与非关系型①关系型数据库管理系统（RDBMS）-----适用于二维表格常见的系统有：oracle/mysql/sqlserver
  • 萱仔求职系列——3.2 力扣面试150题目——数组&字符串第二弹 萱仔学习自我记录 leetcode面试算法
    122.买卖股票的最佳时机II给你一个整数数组prices，其中prices[i]表示某支股票第i天的价格。在每一天，你可以决定是否购买和/或出售股票。你在任何时候最多只能持有一股股票。你也可以先购买，然后在同一天出售。返回你能获得的最大利润。解法1：贪心算法贪心算法的思想是通过局部最优解来寻找全局最优解。我个人理解的是只要今天的价格比昨天的价格高，我们就可以选择在昨天买入，今天卖出，classS
  • 【每日晨读】 人像摄影进行时：完美构图1 II终生学习II
    我们所拍摄的人物都真实地存在于一种空间中，不管他（她）所在的空间环境是复杂还是简单，他（她）都是具有空间性的。而在摄影中，要想表达空间，真实地还原人物，就一定会涉及透视知识。透视是一种广泛性的存在。正因为它在视觉上具有客观性而无法让人忽视。可以说，每拍摄一幅画面，都无可避免地要对画面的透视关系进行效果上的处理，以使得照片这种二维平面性的视效产生尽可能迷人的空间立体效果。这是照片以二维向三维幻化的必
  • 2020年12月29日 星期二 天气阴有雪 改变自己 夏鸿鹄
    前几天猪头打二维码，在次出现错误。那天上班干活的时候很忙啊！我自己忙不过来，就过来一个同事帮忙，太忙没注意，一垫板放了十六袋。回想之前，领导开会说过了，按照他说的来干活。如果出错了，他来负责。干活不能我们自己想自己怎么样，就怎么样。都要按照说好的规定来干活，不按照规定来干活。如果出事了那就要自己承担罚款，自己承担罚款这一天干的活都白干了，甚至两天的工资都白干。都很长时间没出大错了，有出错的时候，领
  • Leetcode刷题记录分享——数据结构（队列） #200 岛屿数量 三年买房不是梦 Leetcode数据结构leetcode数据结构队列bfs
    Leetcode刷题记录分享——数据结构（队列）PS：刷题两周了，每周天会专门抽出一段时间来刷Leetcode，这学期在学算法设计与分析，根据课程内容，第一周刷动态规划题目，第二周刷的贪心算法。打算从这周开始刷数据结构。数据结构是大二上学期学的了，过去了一年，当时学的也不扎实，现在通过Leetcode理论+实践重新学习一下。我刷Leetcode会先看一下优质解答，肚里没货硬刚也刚不出来，主要是学习
  • 【AI】张量的秩（阶）与矩阵的秩和阶的区别 栏杆拍遍看吴钩 MindSpore人工智能矩阵线性代数mindspore
    在阅读MindSpore文档时，笔者对这段话不太理解，遂求助ChatGPT.矩阵的秩是矩阵中线性无关的行或者列，矩阵的阶就是矩阵中的行数和列数。而张量的秩和阶是一个概念，指的是张量的维度（是1维的，二维的还是高维的）
  • c++使用动态规划求解01背包问题 苓一在学习 算法c++
    -什么是01背包问题？在01背包问题中，因为每种物品只有一个，对于每个物品只需要考虑选与不选两种情况。如果不选择将其放入背包中，则不需要处理。如果选择将其放入背包中，由于不清楚之前放入的物品占据了多大的空间，需要枚举将这个物品放入背包后可能占据背包空间的所有情况。需要注意的是：01背包问题不能使用贪心思想，因为每次选取最大的并不能保证背包刚好装满，遇到01背包问题先找到题目中的“背包”和“物品”，
  • 2024最便宜的打车软件，盘点几款最实用省钱的手机软件 返金app平台高佣返利省钱
    打车软件哪个最好用？小编给大家推荐一些便宜好用的打车软件，主要包括有花小猪打车，返金商城APP等，app内为用户提供了便捷的打车服务，而且还支持不同的打车方式，让你可以轻松出行，平台中还为大家提供了优惠的打车方案，让你可以节省打车费用，有需要的用户快来下载吧。第一名，花小猪打车，不管是新用户还是老用户，通过下方花小猪2024年官方活动二维码进入领取红包，最低10元，最高可获得免单打车，另外打车后还
  • 图解LeetCode——240. 搜索二维矩阵 II 爪哇缪斯
    一、题目编写一个高效的算法来搜索mxn矩阵matrix中的一个目标值target。该矩阵具有以下特性：每行的元素从左到右升序排列。每列的元素从上到下升序排列。二、示例2.1>示例1：【输入】matrix=[[1,4,7,11,15],[2,5,8,12,19],[3,6,9,16,22],[10,13,14,17,24],[18,21,23,26,30]],target=5【输出】true2.2>
  • 原力元宇宙什么项目拉多·奥霍特尼科夫这样讲解 口碑信息传播者
    拉多·奥霍特尼科夫是MetaForce生态系统的创始人，他引领着一个令人兴奋的项目，将现实世界与虚拟世界相融合。在这篇文章中，我们将介绍MetaForce生态系统的两个元素：Uniteverse和触觉，并探讨拉多·奥霍特尼科夫如何通过这些元素为用户提供令人兴奋的游戏体验和赚钱机会。13分钟视频内容讲明白原力元宇宙项目，使用浏览器扫码观看或加微信好友重新获取观看二维码对接微信：ForceZen一、U
  • 扫雷（蓝桥杯） DHX～ 蓝桥杯算法
    题目描述小明最近迷上了一款名为《扫雷》的游戏。其中有一个关卡的任务如下，在一个二维平面上放置着n个炸雷，第i个炸雷(xi,yi,ri)表示在坐标(xi,yi)处存在一个炸雷，它的爆炸范围是以半径为ri的一个圆。为了顺利通过这片土地，需要玩家进行排雷。玩家可以发射m个排雷火箭，小明已经规划好了每个排雷火箭的发射方向，第j个排雷火箭(xj,yj,rj)表示这个排雷火箭将会在(xj,yj)处爆炸，它的爆
  • 做自己，让自己发光 果然越来越好
    很多时候，总想着诗与远方，却忽略了身边的日常。想想，生活其实并不是，每时每刻都耀眼的。大多数人终归是平凡的，但要始终有颗上进的心。生命的规律是爱与平和。若有说不同，那就是每个人的经历不同。所以生命的色彩不同，差异很大。但生命的历程是一样的，都是悟空。从无到有，再到无……人生如茶，总是有浮沉起伏。所以要修好自己的心。平日里自己杂念太多，心里纷纷扰扰，向美是好，然则有些贪心，什么都想做好。一次只做一件
  • 科研绘图系列：R语言柱状图分布（histogram plot） 生信学习者1 SCI科研绘图系列r语言数据可视化
    文章目录介绍加载R包读取数据画图介绍柱状图（BarChart）是一种常用的数据可视化图表，用于展示和比较不同类别或组的数据。它通过在二维平面上绘制一系列垂直或水平的柱子来表示数据的大小，每个柱子的长度或高度代表一个数据点的数值。柱状图非常适合于展示分类数据的分布和比较。柱状图的特点：直观比较：柱状图可以直观地展示不同类别之间的数值比较，易于理解。分类展示：数据按照类别或组别进行分组展示，每个类别用
  • 揭秘GLM-130B爆火秘诀：颠覆性自回归填空和二维位置编码的训练黑科技 大多_C 人工智能
    GLM（通用语言模型）的训练过程确实复杂，尤其是涉及到其独特的预训练目标和架构调整。让我来详细解释一下GLM的训练过程。1.模型架构简介GLM-130B是基于Transformer架构的双语（中文和英文）语言模型，拥有1300亿个参数。与常见的GPT模型不同，GLM采用了一种独特的自回归空白填充预训练目标，以更好地捕捉上下文之间的关系。2.预训练过程概述GLM的预训练过程可以分为三个主要部分：输入
  • torch.nn中的22种loss函数简述 01_6 人工智能机器学习
    loss.py中能看到所有的loss函数，本文会简单对它们进行介绍1.L1Loss计算输入和目标之间的L1（即绝对值）损失。这种损失函数会计算预测值和目标值之间差的绝对值的平均。2.NLLLoss(负对数似然损失)首先找到每个样本模型预测的概率分布中对应于真实标签的那个值，然后取这个值的负数，最后对所有样本的损失取平均。即loss(x,class)=−x[class]3.NLLLoss2d(二维输
  • 线性代数|机器学习-P33卷积神经网络ImageNet和卷积规则 取个名字真难呐 算法机器学习矩阵人工智能线性代数
    文章目录1.ImageNet2.卷积计算2.1两个多项式卷积2.2函数卷积2.3循环卷积3.周期循环矩阵和非周期循环矩阵4.循环卷积特征值4.1卷积计算的分解4.2运算量4.3二维卷积公式5.KroneckerProduct1.ImageNetImageNet的论文paper链接如下：详细请直接阅读相关论文即可通过网盘分享的文件：imagenet_cvpr09.pdf链接:https://pan.
  • 【C++前缀和】3212. 统计 X 和 Y 频数相等的子矩阵数量|1672 闻缺陷则喜何志丹 c++力扣算法网格前缀和数量相等
    本文涉及的基础知识点C++算法：前缀和、前缀乘积、前缀异或的原理、源码及测试用例包括课程视频LeetCode3212.统计X和Y频数相等的子矩阵数量难度分：1672给你一个二维字符矩阵grid，其中grid[i][j]可能是‘X’、‘Y’或‘.’，返回满足以下条件的子矩阵数量：包含grid[0][0]‘X’和‘Y’的频数相等。至少包含一个‘X’。示例1：输入：grid=[[“X”,“Y”,“.”]
  • C#基础（4）二维数组 ling1s C#基础c#开发语言
    前言书接上回，我们已经介绍完了一维数组的使用，大抵了解的数组的基础功能和使用方法，现在我们就进入多维数组的讲解。而多维数组中，最常用的有二维数组，我们就以此为例子展开多维数组的讲解。因为其实很多概念我们在一维数组中已经有所解析，所以二维数组我们会讲的稍微快一些。基本概念一维数组是一个下标确定元素。那同理可得，二维数组就是两个下标确定元素，这两个下标我们习惯叫作行标和列标。申明申明方式其实和一维数组
  • 日日新生-空间管理-DAY004 星问
    来自盘点卫生间区域的清洁用品的思考接续上一篇，在盘点中有几件物品引起了思考：第二类：长时间未使用的便携装硅胶盒（装洗发水、沐浴液）2个＋长达11年的吹风机1个第三类：过期的、未曾使用过的牙菌斑测试棒1盒＋面膜1瓶学习用理性的系统来思考和分析：1、当时为什么要买？2、为什么长时间没有使用过？3、过期的物品为什么要保留？回归到一个问题：贪心。便携的硅胶盒及吹风机是考虑出差携带方便、不浪费、环保，事实上
  • python正则表达式(.*?)以及compile的用法示例 测试老孔 pythonpython正则表达式
    在Python开发爬虫过程中经常会遇到正则表达式，其中(.*?)的使用概率较高，那么这个正则表达式到底什么意思呢？“.*?”表示非贪心算法，表示要精确的配对“.*”表示贪心算法，表示要尽可能多的匹配“()”表示要获取括弧之间的信息Python提供re模块，包含所有正则表达式的功能。由于Python的字符串本身也用\转义，所以要特别注意：s='ABC\\-001'#Python的字符串#对应的正则表
  • 雷达图在单细胞数据分析中的应用 周运来就是我
    听过周老师的课的同学，应该有印象：周老师在讲单细胞数据结构的时候提到过，单细胞数据是表达量数据，每个数值表示的是表达量，也就是含量，是一个非负数。表达量这个可以有绝对表达量和相对表达量，也就是所占的比例。基于这个简单淳朴的认知，其实我们就可以画出很多好玩的图，如雷达图。雷达图是以从同一点开始的轴上表示的三个或更多个定量变量的二维图表的形式显示多变量数据的图形方法。今天在逛一个单细胞免疫数据库的时候
  • 地道的经济学思维帮你看到那些本来看不见的事情 一个心理咨询师
    经济学会帮我们点出那些看不到的事情，从选择的角度，从时间的角度，从竞争的角度，从潜在的竞争者有没有入场机会的角度，从成功和失败者的角度。通过这些角度，我们对一件事情从从二维的认知变成三维的认知。当我们看到这些，再去审视真实的世界，发现原来它一直都在，而我之前从来没有看到。继续经济学基础概念。图片发自App第1个产权界定。如何分饼会决定饼能做多大。把土地的经营权、管理权、收入分配权，从大集体那里转向
  • 分享一个基于微信小程序的智慧校园服务平台（源码、调试、LW、开题、PPT） 计算机源码社 微信小程序微信小程序毕业设计项目计算机毕设源码计算机毕设毕设选题课程设计源码毕业设计答辩
    作者：计算机源码社个人简介：本人八年开发经验，擅长Java、Python、PHP、.NET、Node.js、Android、微信小程序、爬虫、大数据、机器学习等，大家有这一块的问题可以一起交流！学习资料、程序开发、技术解答、文档报告如需要源码，可以扫取文章下方二维码联系咨询Java项目微信小程序项目Android项目Python项目PHP项目ASP.NET项目Node.js项目选题推荐项目实战|基
  • Java 并发包之线程池和原子计数 lijingyao8206 Java计数ThreadPool并发包java线程池
    对于大数据量关联的业务处理逻辑，比较直接的想法就是用JDK提供的并发包去解决多线程情况下的业务数据处理。线程池可以提供很好的管理线程的方式，并且可以提高线程利用率，并发包中的原子计数在多线程的情况下可以让我们避免去写一些同步代码。     这里就先把jdk并发包中的线程池处理器ThreadPoolExecutor 以原子计数类AomicInteger 和倒数计时锁C
  • java编程思想 抽象类和接口 百合不是茶 java抽象类接口
    接口c++对接口和内部类只有简介的支持,但在java中有队这些类的直接支持   1 ,抽象类 :  如果一个类包含一个或多个抽象方法,该类必须限定为抽象类(否者编译器报错)   抽象方法 : 在方法中仅有声明而没有方法体    package com.wj.Interface;
  • [房地产与大数据]房地产数据挖掘系统 comsci 数据挖掘
           随着一个关键核心技术的突破,我们已经是独立自主的开发某些先进模块,但是要完全实现,还需要一定的时间...        所以,除了代码工作以外,我们还需要关心一下非技术领域的事件..比如说房地产     &nb
  • 数组队列总结 沐刃青蛟 数组队列
          数组队列是一种大小可以改变，类型没有定死的类似数组的工具。不过与数组相比，它更具有灵活性。因为它不但不用担心越界问题，而且因为泛型（类似c++中模板的东西）的存在而支持各种类型。      以下是数组队列的功能实现代码：   import List.Student; public class
  • Oracle存储过程无法编译的解决方法 IT独行者 oracle存储过程　
    今天同事修改Oracle存储过程又导致2个过程无法被编译，流程规范上的东西，Dave 这里不多说，看看怎么解决问题。   1.     查看无效对象 XEZF@xezf(qs-xezf-db1)> select object_name,object_type,status from all_objects where status='IN
  • 重装系统之后oracle恢复 文强chu oracle
    前几天正在使用电脑，没有暂停oracle的各种服务。 突然win8.1系统奔溃，无法修复，开机时系统 提示正在搜集错误信息，然后再开机，再提示的无限循环中。 无耐我拿出系统u盘 准备重装系统，没想到竟然无法从u盘引导成功。 晚上到外面早了一家修电脑店，让人家给装了个系统，并且那哥们在我没反应过来的时候， 直接把我的c盘给格式化了 并且清理了注册表，再装系统。 然后的结果就是我的oracl
  • python学习二（ 一些基础语法） 小桔子 pthon基础语法
    紧接着把！昨天没看继续看django 官方教程，学了下python的基本语法 与c类语言还是有些小差别： 1.ptyhon的源文件以UTF-8编码格式 2. /   除 结果浮点型 //  除 结果整形 %   除 取余数 *   乘 **  乘方 eg 5**2 结果是5的2次方25 _&
  • svn 常用命令 aichenglong SVN版本回退
    1 svn回退版本   1)在window中选择log,根据想要回退的内容,选择revert this version或revert chanages from this version 两者的区别:   revert this version:表示回退到当前版本(该版本后的版本全部作废)   revert chanages from this versio
  • 某小公司面试归来 alafqq 面试
    先填单子，还要写笔试题，我以时间为急，拒绝了它。。时间宝贵。 老拿这些对付毕业生的东东来吓唬我。。 面试官很刁难，问了几个问题，记录下； 1，包的范围。。。public,private,protect. --悲剧了 2，hashcode方法和equals方法的区别。谁覆盖谁.结果，他说我说反了。 3，最恶心的一道题，抽象类继承抽象类吗？（察，一般它都是被继承的啊） 4，stru
  • 动态数组的存储速度比较 集合框架 百合不是茶 集合框架
    集合框架： 自定义数据结构(增删改查等) package 数组; /** * 创建动态数组 * @author 百合 * */ public class ArrayDemo{ //定义一个数组来存放数据 String[] src = new String[0]; /** * 增加元素加入容器 * @param s要加入容器
  • 用JS实现一个JS对象，对象里有两个属性一个方法 bijian1013 js对象
    <html> <head> </head> <body> 用js代码实现一个js对象，对象里有两个属性，一个方法 </body> <script> var obj={a:'1234567',b:'bbbbbbbbbb',c:function(x){
  • 探索JUnit4扩展：使用Rule bijian1013 java单元测试JUnitRule
            在上一篇文章中，讨论了使用Runner扩展JUnit4的方式，即直接修改Test Runner的实现(BlockJUnit4ClassRunner)。但这种方法显然不便于灵活地添加或删除扩展功能。下面将使用JUnit4.7才开始引入的扩展方式——Rule来实现相同的扩展功能。 1. Rule       &n
  • [Gson一]非泛型POJO对象的反序列化 bit1129 POJO
    当要将JSON数据串反序列化自身为非泛型的POJO时，使用Gson.fromJson(String, Class)方法。自身为非泛型的POJO的包括两种： 1. POJO对象不包含任何泛型的字段 2. POJO对象包含泛型字段，例如泛型集合或者泛型类 Data类 a.不是泛型类， b.Data中的集合List和Map都是泛型的 c.Data中不包含其它的POJO    
  • 【Kakfa五】Kafka Producer和Consumer基本使用 bit1129 kafka
    0.Kafka服务器的配置 一个Broker， 一个Topic Topic中只有一个Partition（）   1. Producer： package kafka.examples.producers; import kafka.producer.KeyedMessage; import kafka.javaapi.producer.Producer; impor
  • lsyncd实时同步搭建指南——取代rsync+inotify ronin47
    1. 几大实时同步工具比较 1.1 inotify + rsync 最近一直在寻求生产服务服务器上的同步替代方案，原先使用的是 inotify + rsync，但随着文件数量的增大到100W+，目录下的文件列表就达20M，在网络状况不佳或者限速的情况下，变更的文件可能10来个才几M，却因此要发送的文件列表就达20M，严重减低的带宽的使用效率以及同步效率；更为要紧的是，加入inotify
  • java-9. 判断整数序列是不是二元查找树的后序遍历结果 bylijinnan java
    public class IsBinTreePostTraverse{ static boolean isBSTPostOrder(int[] a){ if(a==null){ return false; } /*1.只有一个结点时，肯定是查找树 *2.只有两个结点时，肯定是查找树。例如{5,6}对应的BST是 6 {6,5}对应的BST是
  • MySQL的sum函数返回的类型 bylijinnan javaspringsqlmysqljdbc
    今天项目切换数据库时，出错 访问数据库的代码大概是这样： String sql = "select sum(number) as sumNumberOfOneDay from tableName"; List<Map> rows = getJdbcTemplate().queryForList(sql); for (Map row : rows
  • java设计模式之单例模式 chicony java设计模式
    在阎宏博士的《JAVA与模式》一书中开头是这样描述单例模式的： 　　作为对象的创建模式，单例模式确保某一个类只有一个实例，而且自行实例化并向整个系统提供这个实例。这个类称为单例类。 单例模式的结构 　　单例模式的特点： 单例类只能有一个实例。 单例类必须自己创建自己的唯一实例。 单例类必须给所有其他对象提供这一实例。 　　饿汉式单例类   publ
  • javascript取当月最后一天 ctrain JavaScript
    <!--javascript取当月最后一天--> <script language=javascript> var current = new Date(); var year = current.getYear(); var month = current.getMonth(); showMonthLastDay(year, mont
  • linux tune2fs命令详解 daizj linuxtune2fs查看系统文件块信息
    一.简介： tune2fs是调整和查看ext2/ext3文件系统的文件系统参数，Windows下面如果出现意外断电死机情况，下次开机一般都会出现系统自检。Linux系统下面也有文件系统自检，而且是可以通过tune2fs命令，自行定义自检周期及方式。 二.用法： Usage: tune2fs [-c max_mounts_count] [-e errors_behavior] [-g grou
  • 做有中国特色的程序员 dcj3sjt126com 程序员
      从出版业说起 网络作品排到靠前的，都不会太难看，一般人不爱看某部作品也是因为不喜欢这个类型，而此人也不会全不喜欢这些网络作品。究其原因，是因为网络作品都是让人先白看的，看的好了才出了头。而纸质作品就不一定了，排行榜靠前的，有好作品，也有垃圾。 许多大牛都是写了博客，后来出了书。这些书也都不次，可能有人让为不好，是因为技术书不像小说，小说在读故事，技术书是在学知识或温习知识，有
  • Android：TextView属性大全 dcj3sjt126com textview
    android:autoLink    设置是否当文本为URL链接/email/电话号码/map时，文本显示为可点击的链接。可选值(none/web/email/phone/map/all)  android:autoText    如果设置，将自动执行输入值的拼写纠正。此处无效果，在显示输入法并输
  • tomcat虚拟目录安装及其配置 eksliang tomcat配置说明tomca部署web应用tomcat虚拟目录安装
    转载请出自出处：http://eksliang.iteye.com/blog/2097184 1.-------------------------------------------tomcat  目录结构 config：存放tomcat的配置文件 temp  ：存放tomcat跑起来后存放临时文件用的 work   ： 当第一次访问应用中的jsp
  • 浅谈：APP有哪些常被黑客利用的安全漏洞 gg163 APP
    首先，说到APP的安全漏洞，身为程序猿的大家应该不陌生；如果抛开安卓自身开源的问题的话，其主要产生的原因就是开发过程中疏忽或者代码不严谨引起的。但这些责任也不能怪在程序猿头上，有时会因为BOSS时间催得紧等很多可观原因。由国内移动应用安全检测团队爱内测（ineice.com）的CTO给我们浅谈关于Android 系统的开源设计以及生态环境。 1. 应用反编译漏洞：APK 包非常容易被反编译成可读
  • C#根据网址生成静态页面 hvt Web.netC#asp.nethovertree
    HoverTree开源项目中HoverTreeWeb.HVTPanel的Index.aspx文件是后台管理的首页。包含生成留言板首页，以及显示用户名，退出等功能。根据网址生成页面的方法：   bool CreateHtmlFile(string url, string path) { //http://keleyi.com/a/bjae/3d10wfax.htm stri
  • SVG 教程 （一） 天梯梦 svg
    SVG 简介 SVG 是使用 XML 来描述二维图形和绘图程序的语言。 学习之前应具备的基础知识： 继续学习之前，你应该对以下内容有基本的了解： HTML XML 基础 如果希望首先学习这些内容，请在本站的首页选择相应的教程。 什么是SVG？ SVG 指可伸缩矢量图形 (Scalable Vector Graphics) SVG 用来定义用于网络的基于矢量
  • 一个简单的java栈 luyulong java数据结构栈
    public class MyStack { private long[] arr; private int top; public MyStack() { arr = new long[10]; top = -1; } public MyStack(int maxsize) { arr = new long[maxsize]; top
  • 基础数据结构和算法八：Binary search sunwinner AlgorithmBinary search
    Binary search needs an ordered array so that it can use array indexing to dramatically reduce the number of compares required for each search, using the classic and venerable binary search algori
  • 12个C语言面试题，涉及指针、进程、运算、结构体、函数、内存，看看你能做出几个！ 刘星宇 c面试
    12个C语言面试题，涉及指针、进程、运算、结构体、函数、内存，看看你能做出几个！ 1.gets()函数 问：请找出下面代码里的问题： #include<stdio.h> int main(void) {     char buff[10];     memset(buff,0,sizeof(buff));
  • ITeye 7月技术图书有奖试读获奖名单公布 ITeye管理员 活动ITeye试读
    ITeye携手人民邮电出版社图灵教育共同举办的7月技术图书有奖试读活动已圆满结束，非常感谢广大用户对本次活动的关注与参与。 7月试读活动回顾： http://webmaster.iteye.com/blog/2092746 本次技术图书试读活动的优秀奖获奖名单及相应作品如下（优秀文章有很多，但名额有限，没获奖并不代表不优秀）： 《Java性能优化权威指南》
按字母分类： ABCDEFGHIJKLMNOPQRSTUVWXYZ其他