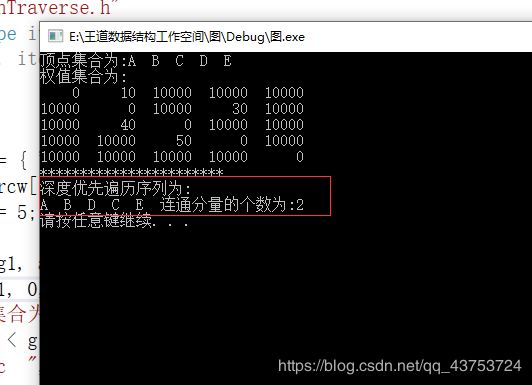
图的连通分量个数
一、定义:
在无向图中,如果从顶点vi到顶点vj有路径,则称vi和vj连通。如果图中任意两个顶点之间都连通,则称该图为连通图,否则,将其中的较大连通子图称为连通分量。
在有向图中,如果对于每一对顶点vi和vj,从vi到vj和从vj到vi都有路径,则称该图为强连通图;否则,将其中的极大连通子图称为强连通分量。
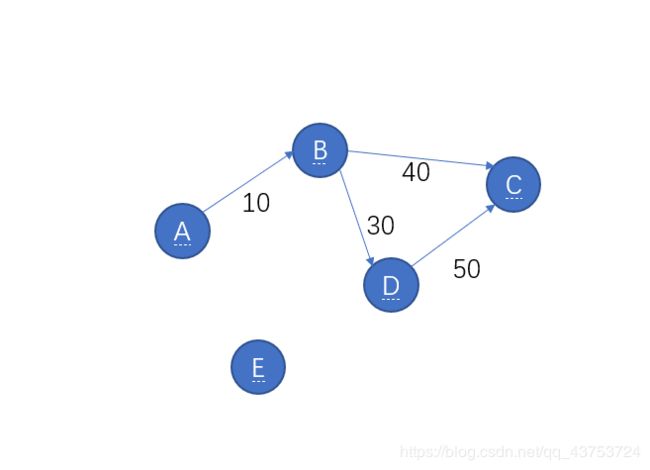
上面有向图的连通分量个数为2
二、分析:
- 我们给图的每个结点设置一个访问标志,用visited[]数组来表示,0代表未访问,1代表已经访问
- 然后我们求从每个节点开始的深度优先遍历序列,每访问到一个结点,就将该结点对应的visited[]置1.
- 若当前结点已经被访问过(也就是visited[]数组中对应位置为1),那这个结点就不用再深度优先遍历,
- 只有visited[]对应位置为0时才在当前结点进行深度优先遍历,深度优先遍历的次数就是该图的连通分量个数。
三、核心算法:
typedef struct {
DataType list[MaxSize];
int size;
}SeqList;
typedef struct {
SeqList Vertices; //存放顶点的顺序表
int edge[MaxVertices][MaxVertices];//存放边的邻接矩阵
int numOfEdges; //边的条数
}AdjMGraph; //图的结构体定义
//这里假设图的顶点信息为字母类型
//连通图的深度优先遍历函数
void DepthFSearch(AdjMGraph G, int v, int visited[], void Visit(DataType item)) {
//连通图G以v为顶点的、访问操作为Visit()的深度优先遍历
//数组visited标记相应顶点是否已访问过(0表示未访问,1表示已访问)
int w;
Visit(G.Vertices.list[v]);//访问顶点v
visited[v] = 1; //置已被访问标记
w = GetFirstVex(G,v);//取第一个邻接顶点
while (w != -1) {
if (!visited[w])
DepthFSearch(G, w, visited, Visit); //递归
w = GetNextVex(G, v, w); //取下一个邻接顶点
}
}
//非连通图的深度优先遍历函数(返回值为连通分量的个数)
int DepthFirstSearch(AdjMGraph G, void Visit(DataType item))
//非连通图G的访问操作为Visit()的深度优先遍历
{
int i;
int count = 0;
int *visited = (int *)malloc(sizeof(int)*G.Vertices.size);
for (i = 0; i < G.Vertices.size; i++) {
visited[i] = 0;
}
for (i = 0; i < G.Vertices.size; i++) {
if (!visited[i]){
count++;//统计连通分量的个数
DepthFSearch(G, i, visited, Visit);//以每个顶点为初始顶点进行调用
}
}
free(visited);
return count;
}
四、完整代码:
下面这个是有向图的代码,若要改为无向图,就将插入点和插入边的函数修改就行。
AdjMGraph.h:
#pragma once
//图的邻接矩阵存储结构
#include "SeqList.h"
typedef struct {
SeqList Vertices; //存放顶点的顺序表
int edge[MaxVertices][MaxVertices];//存放边的邻接矩阵
int numOfEdges; //边的条数
}AdjMGraph; //图的结构体定义
//初始化
void Initiate(AdjMGraph *G, int n)
{
int i, j;
for(i=0;iedge[i][j] = 0;
}
else {
G->edge[i][j] = MaxWeight; //MaxWeight表示无穷大
}
}
G->numOfEdges = 0; //边的条数置零
ListInitiate(&G->Vertices); //顺序表初始化
}
//插入顶点
void InsertVertex(AdjMGraph *G, DataType vertex) {
//在途中插入顶点Vertex
ListInsert(&G->Vertices, G->Vertices.size, vertex);//在顺序表尾部插入
}
/*
插入边
在有向图中插入一条有向边。对于增加无向边的操作,可通过增加两条有向边完成。
*/
void InsertEdge(AdjMGraph *G, int v1, int v2, int weight) {
//在图中插入边,边的权为weight
if (v1 < 0 || v1 >= G->Vertices.size || v2 < 0 || v2 >= G->Vertices.size) {
printf("参数v1或v2越界出错!\n");
return;
}
G->edge[v1][v2] = weight;
G->numOfEdges++;
}
/*
删除边
在图中删除一条有向边。对于删除无向边的操作,可通过取消两条有向边完成
*/
void DeleteEdge(AdjMGraph *G, int v1, int v2) {
//在图中删除边
if (v1 < 0 || v1 >= G->Vertices.size || v2 < 0 || v2 >= G->Vertices.size || v1 == v2) {
printf("参数v1或者v2越界出错!\n");
return;
}
if (G->edge[v1][v2] == MaxWeight || v1 == v2) {
printf("该边不存在!\n");
return;
}
G->edge[v1][v2] = MaxWeight;
G->numOfEdges--;
}
/*
取第一个邻接顶点
对于邻接矩阵来说,顶点v的第一个邻接顶点,就是邻接矩阵的顶点v行中
从第一个矩阵元素开始的非0且非无穷大的顶点
*/
int GetFirstVex(AdjMGraph G, int v)
//在图G中寻找序号为v的顶点的第一个邻接顶点
//如果这样的邻接顶点存在,则返回该邻接顶点的序号,否则返回-1
{
int col;
if (v < 0 || v >= G.Vertices.size) {
printf("参数v1越界出错");
return -1;
}
else {
for (col = 0; col < G.Vertices.size; col++) {
if (G.edge[v][col] > 0 && G.edge[v][col] < MaxWeight)
return col;
}
return -1;
}
}
/*
取下一个邻接顶点
对于邻接矩阵存储结构来说,顶点v1的邻接顶点v2的下一个邻接顶点,就是邻接矩阵的顶点
v行中从第v2+1个矩阵元素开始的非0且非无穷大的顶点
*/
int GetNextVex(AdjMGraph G, int v1, int v2) {
//在图中寻找v1的顶点的邻接顶点v2的下一个邻接顶点
//如果这样的邻接顶点存在,则返回该邻接顶点的序号,否则返回-1
//v1和v2都是相应顶点的序号
int col;
if (v1 < 0 || v1 >= G.Vertices.size || v2 < 0 || v2 >= G.Vertices.size) {
printf("参数v1或v2越界出错!\n");
return -1;
}
for (col = v2 + 1; col < G.Vertices.size; col++) {
if (G.edge[v1][col] > 0 && G.edge[v1][col] < MaxWeight)
return col;
}
return -1;
}
AdjMGraphCreate.h
#pragma once
#include "AdjMGraph.h"
typedef struct {
int Row; //行下标
int col; //列下标
int weight; //权值
}RowColWeight; //边信息结构体定义
void CreateGraph(AdjMGraph *G, char V[], int n, RowColWeight E[], int e) {
//在图G中插入n个顶点信息V和e条边信息E
int i, k;
Initiate(G, n); //顶点顺序表初始化
for (i = 0; i < n; i++)
InsertVertex(G, V[i]);//插入顶点
for (k = 0; k < e; k++)
InsertEdge(G, E[k].Row, E[k].col, E[k].weight);//插入边
}
AdjMGraphTraverse.h
#pragma once
#include"AdjMGraph.h"
#include"SeqList.h"
//这里假设图的顶点信息为字母类型
//连通图的深度优先遍历函数
void DepthFSearch(AdjMGraph G, int v, int visited[], void Visit(DataType item)) {
//连通图G以v为顶点的、访问操作为Visit()的深度优先遍历
//数组visited标记相应顶点是否已访问过(0表示未访问,1表示已访问)
int w;
Visit(G.Vertices.list[v]);//访问顶点v
visited[v] = 1; //置已被访问标记
w = GetFirstVex(G,v);//取第一个邻接顶点
while (w != -1) {
if (!visited[w])
DepthFSearch(G, w, visited, Visit); //递归
w = GetNextVex(G, v, w); //取下一个邻接顶点
}
}
//非连通图的深度优先遍历函数(返回值为连通分量的个数)
int DepthFirstSearch(AdjMGraph G, void Visit(DataType item))
//非连通图G的访问操作为Visit()的深度优先遍历
{
int i;
int count = 0;
int *visited = (int *)malloc(sizeof(int)*G.Vertices.size);
for (i = 0; i < G.Vertices.size; i++) {
visited[i] = 0;
}
for (i = 0; i < G.Vertices.size; i++) {
if (!visited[i]){
count++;//统计连通分量的个数
DepthFSearch(G, i, visited, Visit);//以每个顶点为初始顶点进行调用
}
}
free(visited);
return count;
}
SeqList.h
#pragma once
typedef struct {
DataType list[MaxSize];
int size;
}SeqList;
//初始化
void ListInitiate(SeqList *L) {
L->size = 0;
}
//求当前数据元素个数
int ListLength(SeqList L) {
return L.size;
}
//插入数据元素
int ListInsert(SeqList *L, int i, DataType x) {
//在顺序表的第i个位置(0<=i<=size)个位置前插入数据元素值x
//插入成功返回1,插入失败返回0
int j;
if (L->size >= MaxSize) {
printf("顺序表已满无法插入!");
return 0;
}
else if (i<0 || i>L->size) {
printf("参数i不合法!\n");
return 0;
}
else {
//从后向前依次后移数据,为插入做准备
for (j = L->size; j > i; j--) {
L->list[j] = L->list[j - 1];
}
L->list[i] = x;
L->size++;
return 1;
}
}
//删除数据元素
int ListDelete(SeqList *L, int i, DataType *x) {
//删除顺序表L中第i(0<=i<=size-1)个位置处的数据元素并保存到x中
//删除成功返回1,删除失败返回0
int j;
if (L->size <= 0) {
printf("顺序表已空无法删除!\n");
return 0;
}
else if (i<0 || i>L->size - 1) {
printf("参数i不合法");
return 0;
}
else {
*x = L->list[i];//保存删除的元素到x中
//从前向后依次前移
for (j = i + 1; j <= L->size - 1; j++) {
L->list[j - 1] = L->list[j];
}
L->size--;
return 1;
}
}
//取数据元素
int ListGet(SeqList L, int i, DataType *x) {
//取顺序表的第i个数据元素存于x中,成功返回1,失败返回0
if (i<0 || i>L.size - 1) {
printf("参数i不合法!");
return 0;
}
else {
*x = L.list[i];
return 1;
}
}
test.cpp:
#pragma once
#include
#include
typedef char DataType;
#define MaxSize 10
#define MaxVertices 10
#define MaxWeight 10000
#include "SeqList.h"
#include "AdjMGraph.h"
#include "AdjMGraphCreate.h"
#include"AdjMGraphTraverse.h"
void Visit(DataType item) {//定义访问操作函数
printf("%c ", item);
}
int main() {
AdjMGraph g1;
DataType a[] = { 'A','B','C','D','E' };
RowColWeight rcw[] = { {0,1,10},{0,4,20},{1,3,30},{2,1,40},{3,2,50} };
int n = 5, e = 5;
int i, j;
CreateGraph(&g1, a, n, rcw, e);
//DeleteEdge(&g1, 0, 4);//删除边<0,4>
printf("顶点集合为:");
for (i = 0; i < g1.Vertices.size; i++) {
printf("%c ", g1.Vertices.list[i]);
}
printf("\n");
printf("权值集合为:\n");
for (i = 0; i < g1.Vertices.size; i++) {
for (j = 0; j < g1.Vertices.size; j++) {
printf("%5d ", g1.edge[i][j]);
}
printf("\n");
}
printf("***********************\n");
printf("深度优先遍历序列为:\n");
int count=DepthFirstSearch(g1,Visit);
printf("连通分量的个数为:%d\n", count);
system("pause");
}