推荐系统实践(三)ICF和UCF
ICF和UCF
一、原理
ICF是基于物品的推荐(利用物品之间的相似度计算预测值)
UCF是基于用户的最近邻推荐
1.UCF
(1)输入:An×m的评分 (用户n,物品m)
(2)1.计算用户之间的相关系数person系数:(得到的值在-1~1之间,越接近1的越好)

得到与A用户近似的N个用户。
person系数的理解:在计算中不考虑平均值的差异使得用户间可以比较。
没有考虑两用户是否仅同时对很少的物品进行评分, 解决办法:重要性赋权
没考虑很多领域会存在一些所有人都喜爱的物品,让两个用户对争议的物品达到共识会比广受换烟的物品达到共识更有价值。 解决办法:对物品评分变换,降低对广受欢迎物品有相同看法的相对重要性,用方差权重因子
选择近邻: 用户相似度定义一个具体的阈值,或者讲规模大小限制为一个固定值,只考虑k个最邻近。
阈值过过高,邻近规模小;阈值过低,邻近规模不会明显降低。
2.欧几里得相似度

3.余弦相似度

Tanimoto相似度:

(3)再用得到用户来近似求解a中对物品p的缺失评分。
用户a对物品p的预测值:pred(a,p)
问题:
1.矩阵太稀疏
2.用户和物品量太大,计算机太大
3.对于新物品,没评分。
2.ICF(1)
(1)输入:An×m的评分 (用户n,物品m)
(2)计算两物品之间的关系,余弦相似度:(没考虑用户平均值差异)

改进版的余弦相似度:

或者:

(3)预测评分:pred(u,p) 与预测物品近邻的物品

数据预处理:
其想法是事先构建一个物品相似度矩阵,描述所有物品两两之间的相似度。在运行时,通过确定与p最相似的物品并计算u对这些邻近物品评分的加权总和来得到用户u对物品p的预测评分。近邻数量受限于当前用户评过分的物品个数。由于这样的物品数量一般都比较少,因此计算预测值可以在线上交互应用允许的短时间内完成。
N个物品得到的相似度的矩阵是An×n的 。但实际上项数会极低,而且还可以采取进一步的方法降低复杂度。可选的方案有,仅考虑那些与其他物品同时评分数最少的物品,或者对每个物品只记录有限的近邻。
ICF(2) Slope One
例子:
顾客吃过后,会有相关的星级评分。假设评分如下:
评分 可乐鸡翅 红烧肉
小明 4 5
小红 4 3
小伟 2 3
小芳 3 ?
问题:请猜测一下小芳可能会给“红烧肉”打多少分?
思路:把两道菜的平均差值求出来,可乐鸡翅减去红烧肉的平均偏差:[(4-5)+(4-3)+(2-3)]/3=-0.333。一个新客户比如小芳,只吃了可乐鸡翅评分为3分,那么可以猜测她对红烧肉的评分为:3-(-0.333)=3.333
这就是slope one 算法的基本思路,非常非常的简单。
算法:
Slope One 算法是由 Daniel Lemire 教授在 2005 年提出的一个Item-Based 的协同过滤推荐算法。和其它类似算法相比, 它的最大优点在于算法很简单, 易于实现, 执行效率高, 同时推荐的准确性相对较高。
Slope One算法是基于不同物品之间的评分差的线性算法,预测用户对物品评分的个性化算法。主要两步:
Step1:计算物品之间的评分差的均值,记为物品间的评分偏差(两物品同时被评分);

Step2:根据物品间的评分偏差和用户的历史评分,预测用户对未评分的物品的评分。 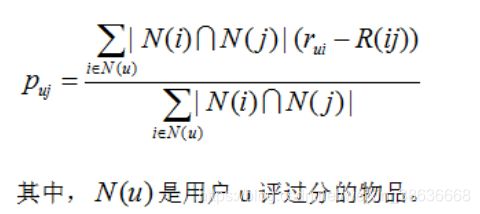
Step3:将预测评分排序,取topN对应的物品推荐给用户。
举例:
假设有100个人对物品A和物品B打分了,R(AB)表示这100个人对A和B打分的平均偏差;有1000个人对物品B和物品C打分了, R(CB)表示这1000个人对C和B打分的平均偏差;

总结:
该算法适用于物品更新不频繁,数量相对较稳定并且物品数目明显小于用户数的场景。依赖用户的用户行为日志和物品偏好的相关内容。
优点:
1.算法简单,易于实现,执行效率高;
2.可以发现用户潜在的兴趣爱好;
缺点:
依赖用户行为,存在冷启动问题和稀疏性问题。
二、代码:
1.ICF
使用的Movie数据集:(主函数)
# 为用户3推荐未看过的10个电影
if __name__ == "__main__":
cf = ItemBasedCF("./data/ml-100k/u.data")
cf.ItemSimilarity()
print(cf.Recommend("3"))
(1)读取数据,并转成字典形式
def readData(self):
"""
读取文件,并生成用户-物品,测试集
用户-物品的评分表
训练集
"""
self.train = {}
# 打开文件,读取训练集
for line in open(self.train_file):
user, item, score, _ = line.strip().split("\t")
self.train.setdefault(user, {})
self.train[user][item] = int(score)
# print(self.train()) #得到的是字典的形式,例如:'411': {'172': 5, '651': 4}
#print(self.train().items()) #得到的是 dict_items([('411', {'172': 5, '651': 4})])
#print(self.train().keys()) #dict_keys(['411'])
(2)计算相似度:
构造item-item的共现矩阵C,N记录items被多少个不同用户购买。最后相似度计算:self.W[i][j] = cij / (math.sqrt(N[i] * N[j]))
def ItemSimilarity(self):
"""
计算物品之间的相似度
"""
C = {} #items-items矩阵 行为次数的矩阵 共现矩阵
N = {} #记录items被多少个不同用户购买
#遍历训练数据,获取用户对有过行为的物品
for user, items in self.train.items():
#遍历该用户每件物品项
for i in items.keys():
#该物品被用户购买计数加1
if i not in N.keys():
N.setdefault(i, 0)
N[i] += 1
# 物品-物品共现矩阵数据加1
if i not in C.keys():
C.setdefault(i, {})
for j in items.keys():
if i == j:
continue
if j not in C[i].keys():
C[i].setdefault(j, 0)
C[i][j] += 1
#计算相似度矩阵, 计算物品-物品的相似度,余弦相似度
self.W = {}
for i, related_items in C.items():
if i not in self.W.keys():
self.W.setdefault(i, {})
for j, cij in related_items.items():
self.W[i][j] = cij / (math.sqrt(N[i] * N[j]))
return self.W
(3)推荐物品:对给定user的已知item,求出每个item对应的K个最相似的物品,对每个物品,用rank保存最后的相似度×score的值(rank[j] += score * wj,items相似度*score)。最后,返回概率最大的几个物品的值。
#给用户user推荐,前K个相关用户喜欢的
def Recommend(self, user, K=3, N=10):
"""
给用户推荐物品,取相似度最大的K个物品,推荐排名靠前的10个物品
"""
'''
:param user: 用户(str)
:param K: 相似度的前K个 W[item].items()
:param N: 最后算出来的结果的前N个
:return: 返回最后的前N个值 rank
'''
# 用户对物品的偏好值
rank = {}
# 用户产生过行为的物品项和评分
action_item = self.train[user]
#print(action_item) #用户 ‘3’ 行为的数组 {'335': 1, '245': 1, '337': 1,}
for item, score in action_item.items():
# print(sorted(self.W[item].items(), key=lambda x:x[1], reverse=True))
# print("-----------------------------------------------------------------")
# print(sorted(self.W[item].items(), key=lambda x:x[1], reverse=True)[0:K]) #和物品相似度高的前K的物品
#遍历与item最相似的前K个物品,获得这些物品及相似分数
for j, wj in sorted(self.W[item].items(), key=lambda x: x[1], reverse=True)[0:K]:
#若有该物品,跳过
if j in action_item.keys():
continue
if j not in rank.keys():
rank.setdefault(j, 0)
rank[j] += score * wj
return sorted(rank.items(), key=lambda x: x[1], reverse=True)[0:N]
总结:
整体的代码为:
import math
class ItemBasedCF:
def __init__(self, train_file):
"""
初始化对象
"""
self.train_file = train_file
self.readData()
def readData(self):
"""
读取文件,并生成用户-物品,测试集
用户-物品的评分表
训练集
"""
self.train = {}
# 打开文件,读取训练集
for line in open(self.train_file):
user, item, score, _ = line.strip().split("\t")
self.train.setdefault(user, {})
self.train[user][item] = int(score)
# print(self.train()) #得到的是字典的形式,例如:'411': {'172': 5, '651': 4}
#print(self.train().items()) #得到的是 dict_items([('411', {'172': 5, '651': 4})])
#print(self.train().keys()) #dict_keys(['411'])
def ItemSimilarity(self):
"""
计算物品之间的相似度
"""
C = {} #items-items矩阵 行为次数的矩阵 共现矩阵
N = {} #记录items被多少个不同用户购买
#遍历训练数据,获取用户对有过行为的物品
for user, items in self.train.items():
#遍历该用户每件物品项
for i in items.keys():
#该物品被用户购买计数加1
if i not in N.keys():
N.setdefault(i, 0)
N[i] += 1
# 物品-物品共现矩阵数据加1
if i not in C.keys():
C.setdefault(i, {})
for j in items.keys():
if i == j:
continue
if j not in C[i].keys():
C[i].setdefault(j, 0)
C[i][j] += 1
#计算相似度矩阵, 计算物品-物品的相似度,余弦相似度
self.W = {}
for i, related_items in C.items():
if i not in self.W.keys():
self.W.setdefault(i, {})
for j, cij in related_items.items():
self.W[i][j] = cij / (math.sqrt(N[i] * N[j]))
return self.W
#给用户user推荐,前K个相关用户喜欢的
def Recommend(self, user, K=3, N=10):
"""
给用户推荐物品,取相似度最大的K个物品,推荐排名靠前的10个物品
"""
'''
:param user: 用户(str)
:param K: 相似度的前K个 W[item].items()
:param N: 最后算出来的结果的前N个
:return: 返回最后的前N个值 rank
'''
# 用户对物品的偏好值
rank = {}
# 用户产生过行为的物品项和评分
action_item = self.train[user]
#print(action_item) #用户 ‘3’ 行为的数组 {'335': 1, '245': 1, '337': 1,}
for item, score in action_item.items():
# print(sorted(self.W[item].items(), key=lambda x:x[1], reverse=True))
# print("-----------------------------------------------------------------")
# print(sorted(self.W[item].items(), key=lambda x:x[1], reverse=True)[0:K]) #和物品相似度高的前K的物品
#遍历与item最相似的前K个物品,获得这些物品及相似分数
for j, wj in sorted(self.W[item].items(), key=lambda x: x[1], reverse=True)[0:K]:
#若有该物品,跳过
if j in action_item.keys():
continue
if j not in rank.keys():
rank.setdefault(j, 0)
rank[j] += score * wj
return sorted(rank.items(), key=lambda x: x[1], reverse=True)[0:N]
# 为用户3推荐未看过的10个电影
if __name__ == "__main__":
cf = ItemBasedCF("./data/ml-100k/u.data")
cf.ItemSimilarity()
print(cf.Recommend("3"))
2.UCF
1.读取数据data:
def readData(self):
"""
读取文件,并生成用户-物品,测试集
用户-物品的评分表
训练集
"""
self.train={}
for line in open(self.train_file):
user,item,score,_ = line.strip().split('\t') #.strip()移除空格
self.train.setdefault(user,{})
self.train[user][item] = int(score)
#print(self.train()) #得到的是字典的形式,例如:'411': {'172': 5, '651': 4}
self.test = {}
for line in open(self.test_file):
user, item, score, _ = line.strip().split('\t') # .strip()移除空格
self.test.setdefault(user, {})
self.test[user][item] = int(score)
2.求相似度:构造user-user的共线矩阵,并求解相似度:self.W[u][v] = cuv / math.sqrt(N[u] * N[v])
def UserSimilarity(self):
self.item_users = {} #item和user关系矩阵
for user, items in self.train.items():
for i in items.keys():
if i not in self.item_users.keys():
self.item_users.setdefault(i, set())
self.item_users[i].add(user)
# print(self.item_users) #得到每一个Item 有多少个User使用
C = {} #User 和User的共线矩阵
N = {} #Item中 user出现几次
# Cor = {} #关系矩阵
for i, users in self.item_users.items():
for u in users:
if u not in N.keys():
N.setdefault(u, 0)
N[u] += 1
if u not in C.keys():
C.setdefault(u, {})
for v in users:
if u == v:
continue
if v not in C[u].keys():
C[u].setdefault(v, 0)
C[u][v] += 1
# #生成关系矩阵Cor
# if u not in Cor.keys():
# Cor.setdefault(u,[])
# for v in users:
# if u == v:
# continue
# Cor[u].append(v)
# #print(Cor[u])
3.推荐:给定user,求出user对应的K个最近似的user,对每个user有其对应的items,用rank保存最后的相似度×score(也就是rvi)的值(rank[i] += rvi * wuv用户相似度*score)最后,返回概率最大的几个物品的值。
def Recommend(self,user,K=3,N=10):
'''
:param user:
:param K:
:param N:
:return:
'''
rank = {}
action_item = self.train[user].keys() # 找到用互‘3’的行为商品
for v, wuv in sorted(self.W[user].items(), key=lambda x: x[1], reverse=True)[0:K]:
for i, rvi in self.train[v].items():
if i in action_item:
continue
if i not in rank.keys():
rank.setdefault(i, 0)
rank[i] += rvi * wuv
return sorted(rank.items(), key=lambda x: x[1], reverse=True)[0:N]
主函数:
if __name__=='__main__':
cf = UserBasedCF('./data/ml-100k/u.data','./data/ml-100k/u.data')
print(cf.Recommend('3'))
ICF(2)Slope One
def loadData():
items={'A':{1:5,2:3},
'B':{1:3,2:4,3:2},
'C':{1:2,3:5}}
users={1:{'A':5,'B':3,'C':2},
2:{'A':3,'B':4},
3:{'B':2,'C':5}}
return items,users
#***计算物品之间的评分差
#items:从物品角度,考虑评分
#users:从用户角度,考虑评分
def buildAverageDiffs(items,users,averages):
#遍历每条物品-用户评分数据
for itemId in items:
for otherItemId in items:
average=0.0 #物品间的评分偏差均值
userRatingPairCount=0 #两件物品均评过分的用户数
if itemId!=otherItemId: #若无不同的物品项
for userId in users: #遍历用户-物品评分数
userRatings=users[userId] #每条数据为用户对物品的评分
#当前物品项在用户的评分数据中,且用户也对其他物品由评分
if itemId in userRatings and otherItemId in userRatings:
#两件物品均评过分的用户数加1
userRatingPairCount+=1
#评分偏差为每项当前物品评分-其他物品评分求和
average+=(userRatings[otherItemId]-userRatings[itemId])
averages[(itemId,otherItemId)]=average/userRatingPairCount
#***预测评分
#users:用户对物品的评分数据
#items:物品由哪些用户评分的数据
#averages:计算的评分偏差
#targetUserId:被推荐的用户
#targetItemId:被推荐的物品
def suggestedRating(users,items,averages,targetUserId,targetItemId):
runningRatingCount=0 #预测评分的分母
weightedRatingTotal=0.0 #分子
for i in users[targetUserId]:
#物品i和物品targetItemId共同评分的用户数
ratingCount=userWhoRatedBoth(users,i,targetItemId)
#分子
weightedRatingTotal+=(users[targetUserId][i]-averages[(targetItemId,i)])\
*ratingCount
#分母
runningRatingCount+=ratingCount
#返回预测评分
return weightedRatingTotal/runningRatingCount
# 物品itemId1与itemId2共同有多少用户评分
def userWhoRatedBoth(users,itemId1,itemId2):
count=0
#用户-物品评分数据
for userId in users:
#用户对物品itemId1与itemId2都评过分则计数加1
if itemId1 in users[userId] and itemId2 in users[userId]:
count+=1
return count
if __name__=='__main__':
items,users=loadData()
averages={}
#计算物品之间的评分差
buildAverageDiffs(items,users,averages)
#预测评分:用户2对物品C的评分
predictRating=suggestedRating(users,items,averages,2,'C')
print ('Guess the user will rate the score :',predictRating)
ICF,UCF的区别:
Item CF 和 User CF两个方法都能很好的给出推荐,并可以达到不错的效果。但是他们之间还是有不同之处的,而且适用性也有区别。
1.计算复杂度方面:
在电商平台上,用户数量超级多: ItemCF时间复杂度低
在新闻推荐方面:UCF低
2.适用场景:
社交网络上 UCF更加具有解释性。比如我知道我的某个同学买了,我就会买
基于内容的推荐上 ICF更具有解释性。
参考:
https://blog.csdn.net/xidianliutingting/article/details/51916578