图论算法——加权有向图的数据结构

引言

要解决最短路径问题，先引入加权有向图的数据结构。这和 加权无向图的数据结构很类似。

有关概念可参考博文数据结构之图的概述

加权有向边

package com.algorithms.graph;

/**
 * @author yjw
 * @date 2019/6/5/005
 */
public final class DirectedEdge {
    /**
     * 边的起点
     */
    private final int v;
    /**
     * 边的终点
     */
    private final int w;

    /**
     * 边的权重
     */
    private final double weight;

    public DirectedEdge(int v, int w, double weight) {
        this.v = v;
        this.w = w;
        this.weight = weight;
    }

    public double weight() {
        return weight;
    }

    public int from() {
        return v;
    }

    public int to() {
        return w;
    }

    @Override
    public String toString() {
        return String.format("%d -> %d(%.2f)", v, w, weight);
    }
}

加权有向图

package com.algorithms.graph;

import java.util.HashSet;
import java.util.Set;

/**
 * @author yjw
 * @date 2019/6/5/005
 */
@SuppressWarnings("unchecked")
public class EdgeWeightedDigraph {
    private final int vertexNum;
    private int edgeNum;
    private Set<DirectedEdge>[] adj;

    public EdgeWeightedDigraph(int vertexNum) {
        this.vertexNum = vertexNum;
        this.edgeNum = 0;
        adj = (Set<DirectedEdge>[]) new HashSet[vertexNum];
        for (int v = 0; v < vertexNum; v++) {
            adj[v] = new HashSet<>();
        }
    }

    public int vertexNum() {
        return vertexNum;
    }

    public int edgeNum() {
        return edgeNum;
    }

    public void addEdge(DirectedEdge e) {
        if (adj[e.from()].add(e)) {
            edgeNum++;
        }
    }

    public void addEdge(int start,int end,double weight) {
        addEdge(new DirectedEdge(start,end,weight));
    }

    //提供增加边的便利方法

    /**
     * 以同一起点增加两条边
     */
    public void addEdges(int start,int end1,double weight1,int end2,double weight2) {
        addEdge(start,end1,weight1);
        addEdge(start,end2,weight2);
    }

    /**
     * 增加三条边
     */
    public void addEdges(int start,int end1,double weight1,
                         int end2,double weight2,
                         int end3,double weight3) {
        addEdges(start,end1,weight1,end2,weight2);
        addEdge(start,end3,weight3);
    }


    /**
     * 增加四条边
     */
    public void addEdges(int start,int end1,double weight1,
                         int end2,double weight2,
                         int end3,double weight3,
                         int end4,double weight4) {
        addEdges(start,end1,weight1,end2,weight2,end3,weight3);
        addEdge(start,end4,weight4);
    }

    /**
     * 增加五条边
     */
    public void addEdges(int start,int end1,double weight1,
                         int end2,double weight2,
                         int end3,double weight3,
                         int end4,double weight4,
                         int end5,double weight5) {
        addEdges(start,end1,weight1,end2,weight2,end3,weight3,end4,weight4);
        addEdge(start,end5,weight5);
    }

    public Iterable<DirectedEdge> adj(int v) {
        return adj[v];
    }

    public Iterable<DirectedEdge> edges() {
        Set<DirectedEdge> set = new HashSet<>();
        for (int v = 0; v < vertexNum; v++) {
            set.addAll(adj[v]);
        }
        return set;
    }

    @Override
    public String toString() {
        StringBuilder s = new StringBuilder("(" + vertexNum + " vertices, " + edgeNum + " edges)\n");
        for (int v = 0; v < vertexNum; v++) {
            s.append(v).append(": ");
            for (DirectedEdge e: this.adj(v)) {
                s.append(e).append(" ");
            }
            s.append("\n");
        }
        return s.toString();
    }
}

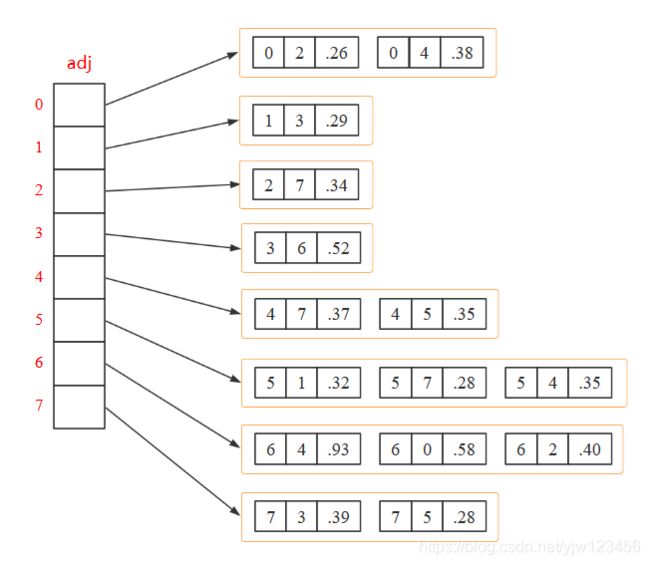
我们就来通过这个类构造上面这个图吧，构造代码：

EdgeWeightedDigraph g = new EdgeWeightedDigraph(8);
g.addEdges(0,2,.26,4,.38);
g.addEdge(1,3,.29);
g.addEdge(2,7,.34);
g.addEdge(3,6,.52);
g.addEdges(4,7,.37,5,.35);
g.addEdges(5,1,.32,7,.28,4,.35);
g.addEdges(6,4,.93,0,.58,2,.40);
g.addEdges(7,3,.39,5,.28);

System.out.println(g);

输出为：

(8 vertices, 15 edges)
0: 0 -> 2(0.26) 0 -> 4(0.38) 
1: 1 -> 3(0.29) 
2: 2 -> 7(0.34) 
3: 3 -> 6(0.52) 
4: 4 -> 5(0.35) 4 -> 7(0.37) 
5: 5 -> 4(0.35) 5 -> 1(0.32) 5 -> 7(0.28) 
6: 6 -> 4(0.93) 6 -> 0(0.58) 6 -> 2(0.40) 
7: 7 -> 5(0.28) 7 -> 3(0.39)