更高的因子有效性评价标准

文献来源: Campbell R. Harvey, Yan Liu, Heqing Zhu.(2016) … and the Cross-Section of Expected Returns [J]. The Review of Financial Studies, 29, 5-68.

推荐原因：数百篇文献以及它们所发现的因子都试图去解释横截面上的期望收益率。由于目前大规模的数据挖掘，继续使用过去通常的标准去确定是否显著就不再合理，那么目前的研究应该使用怎样的临界值？本文引入了一个新的多重检验框架并且提供了从1967年第一个实证检验开始到现在的历史临界值。一个新的因子需要超过更高的临界值，也就是t统计量大于3.0才能被认为有效。因此，我们认为大多数金融经济学研究上发现的新因子可能并不是真正有效。

1、引言

数百篇文献以及它们所发现的因子都试图去解释横截面上的期望收益率。由于目前大规模的数据挖掘，继续使用过去通常的标准去确定是否显著就不再合理，那么目前的研究应该使用怎样的临界值？本文引入了一个新的多重检验框架并且提供了从1967年第一个实证检验开始到现在的历史临界值。一个新的因子需要超过更高的临界值，也就是t统计量大于3.0才能被认为有效。因此，我们认为大多数金融经济学研究上发现的新因子可能并不是真正有效。

2、文献综述

四十多年前，对资本资产定价模型（CAPM）进行的检验发现，市场beta是对横截面上预期收益的显著的解释变量。据报道，Fama和MacBeth的t统计量为2.57,超过了通常的临界值2.0。但是，自那时以来，已有数百篇论文试图解释预期收益的横截面。由于已知因子数量增多，并且我们合理地假设还有更多已被检验但未被公布的因子，因此通常用于显著性检验的临界水平就不再合理。我们提出一个新的框架，该框架可以进行多重检验，且能为当前的资产定价研究产生推荐的统计显著水平

我们从研究横截面上的收益率的期刊中选择313篇作为研究的开始。我们提供了从1967年第一次实证检验开始一直到现今为止每年我们推荐的检验临界值，并且在假设新的因子挖掘的速度和过去十年相同的基础上预测了一直到2032年的t检验临界值。我们还提出了历史因子的分类方法。我们的工作集中在给定对其他因子检验结果的基础上估计新因子的统计显著性，所以我们的目标是用一个多重检验的框架来重新评估过去的研究，同时也能为现在和未来的研究提供一个基准。

我们从频率论的角度来处理多重检验问题。尽管贝叶斯方法也可以用来处理多重检验和变量选择的问题，但是数据的高维，而且无法观察到所有被检验的因子，这为我们使用贝叶斯方法提出了很大的挑战。所以，我们最后提出了一个频率论的方法来解决数据缺失问题，因为并不清楚如何在贝叶斯框架下解决这个问题。

我们的框架也有局限性。首先，所有因子的发现是否应该一视同仁?我们的答案是不应该。从经济学的理论中产生的因子应该比完全从实证中得到的因子有一个更低的阈值，因为经济理论是基于经济原理的，数据挖掘的空间较小。尽管如此，无论新的发现是来自理论中还是实证中，2.0的t统计量都太低。其次，我们的检验的重点是无条件检验，尽管无条件检验可能会考虑因子的边际因素，还是有可能出现该因子在特定经济环境中比较重要而在其他环境中并不重要的情况。所以，在为现在的资产定价研究使用我们推荐的显著水平时需要考虑这2个问题。

3、数据准备和模型方法

3.1 数据来源

我们的目的不是纵览所有发表的关于资产定价的文献，所以我们的关注只限于提出并检验了新因子的文章。例如，Sharpe(1964) ,Lintner(1965)和Mossin(1966)几乎同时从理论上提出了单因子模型-CAPM。随后，数百篇论文都对CAPM进行了检验。我们的研究只涉及理论的文献以及第一篇对CAPM进行检验的文献而没有包含那些在不同情况下对CAPM进行检验的论文。因为我们关注点集中在能很泛化地解释收益率的因子上，所以我们忽略了那些研究集中于一小部分股票和一小段时间的文献。此外，一些理论性的模型缺乏实证检验，尽管如果找到了合适的指标，他们都够被实证验证，我们还是选择忽略他们。

基于这些标准，我们把我们的研究范围缩小到金融，经济和会计领域的顶刊。为了包含最新的研究，我们还包含了一些已经在或者即将在顶会上展示的工作论文。最终我们的研究集中在313篇文章上，其中250篇是发表的论文，63篇是工作论文。

我们最终收集了316个因子，但是很可能低估了因子的数量。首先，我们只考虑顶刊，其次，我们是选择了一小部分工作论文，再者，对同一特征有很多变形的因子，我们是包含了最有代表性的。最后，也是最重要的，我们要估计所有被检验的因子数量，因为有一些没有通过检验的因子没有被公开，我们是无法观察到的。所以，我们的多重检验框架试图去考虑这种可能性。

3.2 因子分类

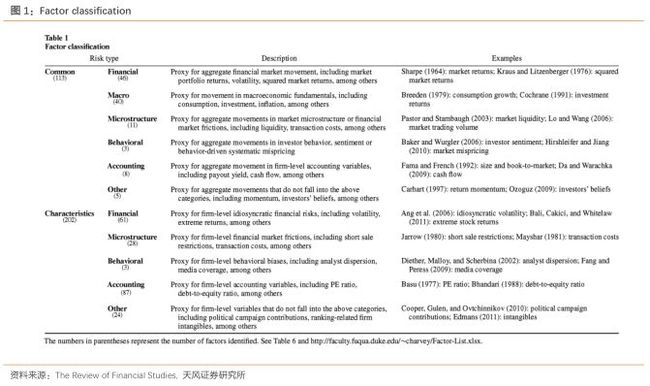
为了便于我们分析，我们把因子分类。我们先宽泛地分成公共因子和个体的特征因子。公共因子是对共同的风险来源的一个评价指标。在这种因子上的风险暴露可以帮助我们解释横截面上的因子收益率的特点。而特质因子表示这种因子是针对特定的证券或者组合有效。

严格来说，风险因子是一个随着时间变化有着我们无法预测的变化的变量，进一步来说，资产在该因子上的风险暴露需要能够用来解释横截面上的收益率的特点。基于这个标准，个体的特征因子就不能被归为风险因子，因为这些特征是已知的而且有着有限的时间序列上的变化。但是，如果我们从更广义的概念上去理论特征因子的话，如果发现某个个体的特征与横截面上的预期收益率相关，通常可以构建多空投资组合以代表潜在的未知风险因子。当我们将特定的个体特征归类为风险因子时，这个未知的风险因子正是我们要考虑的因子。

基于这些因子的性质，我们可以对风险因子和特征因子进一步分类。具体来说，我们把共同因子分类为金融，宏观，微观结构，行为，会计和其他。特征因子也是同样的分类，除了没有宏观这一分类。表1提供了这些子类的详细定义。

3.3 模型方法-多重检验中的t统计量调整

考虑到有如此众多的文章都试图去解释同一个横截面上的预期收益率，统计推断就不应该基于单检验。当只有一个假设被检验时，我们用单检验来表示，而我们的目标是使用多重检验的框架为确定合适的显著水平提供一个指导。

我们注意到偏差的存在，在很多其他领域，顶刊上会也会出现重复研究，也就是说，一个新的因子被发现了，其他人会试图去复现它。但是在金融和经济领域，重复性研究是很难发表的，所以就存在对发表新因子的偏好，而不是去验证已发现因子的存在。通常有两种方法去解决这个偏差问题，一种是样本外验证，另一种就是使用一个可以进行多重检验的统计框架。如果可行的话，样本外验证是最简单的排除假的有效因子的方法，但是样本外验证有一个很重要的缺陷，它不能被用于实际的时间数据中。为了做样本外验证，我们通常需要留出一部分数据，但是对研究者来说，所有的数据都是可观察的，那我们就需要未来的数据，也就是说我们需要很多年的数据去做样本外验证，而这是不现实的，所以我们选择使用多重检验的框架因为它能为判断一个被发现的因子是否真实提供了直接的指导。

在统计学中，多重检验是指同时对多个假设进行检验。多重检验在统计学和医学领域都是很热门的研究方向。尽管多重检验方法有着非常快速的发展，他们还没有在金融研究领域引起关注，即使是已有的用到多重检验的金融研究也局限于使用Bonferroni调整这一过于严格的方法。所以我们的文章试图去填补这一空白。

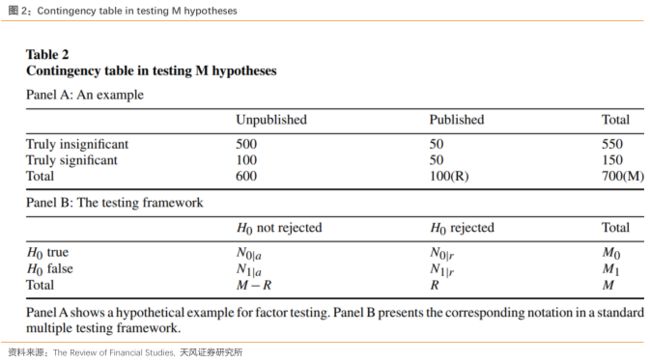
表2中我们为多重检验可能的结果进行了分类。图表A展示了结果，而图表B将A中的结果符号化以便于后续对第一类错误的定义。

我们的图表A假设有100个公布的有效因子（用R表示），其中50个是假阳性，剩下的是真的。此外，研究者还检验了其他600个因子，其中没有一个被检验为显著。其中500个是确实不显著，而剩下100个是真实显著的因子。总共的检验数（M）是700，其中50个因子是假阳性，即犯了第一类错误；而100个实际真实有效的因子因为被归类为不显著因子，没有被公布，即犯了第二类错误。多重检验的目标通常是降低‘50’或者‘50/100’，即假阳性的绝对数量或者相对比例。当然，我们只观察到了已公布的因子，因为被检验过但被发现不显著的因子很少公布。这对我们构成了挑战，因为通常的统计方法仅能处理所有检验结果均可见的情况。

3.4 第一类错误与第二类错误

在单假设检验中，α用来表示控制第一类错误率，也就是一个因子实际不显著却被认为显著的概率，α也被称为显著水平。在多重检验中，限制每个单假设检验的第一类错误类对于控制整体假阳性概率来说是远远不够的，也就是说，在以所有因子都不显著的原假设下，一个具有alpha概率发生的事件在进行很多次因子检验时是很有可能发生的。所以在多重检验中，我们需要对第一类错误的一个衡量来帮助我们同时评估多个单假设检验的结果。

FWER衡量了至少有一个假阳性发生的概率而不考虑检验的总数量。也就是说，研究者检验了100个因子，FWER衡量了错误地把一个或者多个因子认定为显著的概率。在给定显著性水平α，我们尝试了两种方法（Bonferroni和Holm调整）去保证FWER不会超过α。即使检验的个数增长，FWER依然是在衡量至少有一个假阳性的概率。这种绝对的控制和下面我们要定义的比例控制，即flase discovery rate(FDR)是截然不同的。

当我们比较2个显著性水平α相同的检验时，最合理的方法便是比较他们的第二类错误率。但是当我们进行多重检验时，第二类错误率因为依赖于我们未知的参数而难以估计。为了克服这个问题，研究者使用实际第一类错误率和给定的显著性水平之间的差值作为检验过程有有效性的衡量标准。当一个检验的第一类错误率严格小于α时，我们可以通过调高p值的临界值使检验变得宽松从而使得第一类错误率接近于α，由于第一类错误和第二类错误之间相反的关系，第二类错误率在该过程中不断下降。所以，理想情况下，我们希望检验的第一类错误率和给定的显著水平α相同。

FWER和FDR都在科研领域被广泛应用。基于不同的情形，他们被研究者偏好程度会有所不同。当检验数很大的时候，FWER控制的检验过于严格，会导致非常少的阳性结果，研究者会更偏好FDR。而在检验数相对较少的时候，FWER就更多被使用。我们的研究中涉及300多个被公布的因子以及数百个甚至上千个被检验过的因子，但是我们还是不清楚这个数字是否应该被归类为大，这就给我们选择FWER还是FDR带来了困难。在这种情况下，我们选择不去比较这2种衡量指标哪个更合适，而是选择提供FWER和FDR指标下各自调整的p值。研究者可以通过将检验的P值和通过校正得到的临界值比较来观察FDR还是FWER指标被满足。

3.5 P值校正-三种方法

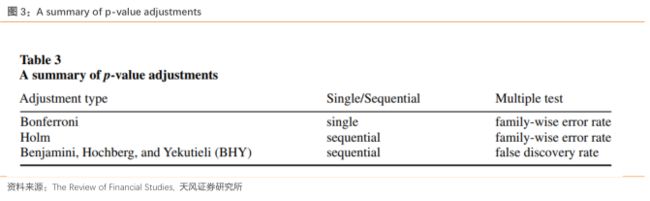
统计学研究已经提出了多种控制FWER和FDR的方法，我们选择最广为人知的三种校正进行介绍：Bonferroni校正，Holm校正以及Benjamini, Hochberg,和Yekutieli(BHY)校正。基于矫正进行的方式，他们被分为两类，单步校正（同等地去校正每个p值）和顺序校正（依赖于p值的整体分布）。Bonferroni校正是单步校正，而Holm和BHY校正是顺序校正。表3总结了三种方法的性质

3.5.1 Bonferroni 校正

3.5.2 Holm 校正

3.5.3 Benjamini, Hochberg,和Yekutieli(BHY)校正

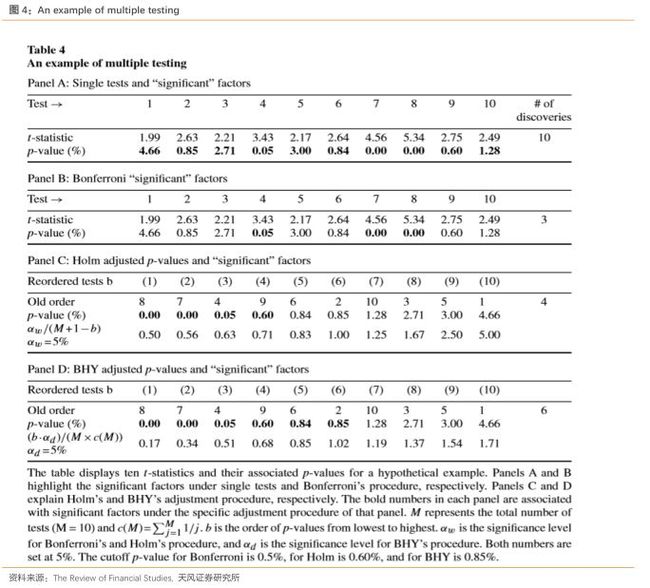
总结以上三个方法，我们发现在单假设检验下，使用通常采用的5%的临界值，10个都被判定被有效因子，使用多重检验的话，p值的临界值会小很多，BHY方法为0.85%，Holm方法为0.6%,Bonferroni方法为0.5%。

图1总结了我们上述的例子，图1画出了原始的p值以及校正后的p值临界值线。我们可以发现尽管十个因子在单假设检验下都被判定为显著有效的因子，但是在多重检验的框架下，只有3到6个因子被判定为显著。这说明尽管单假设检验保证了每个检验第一类错误率满足了给定的显著性水平，但为了满足更加严格的FWER或者FDR的控制，必须丢掉一些因子。

3.6 汇总统计数据

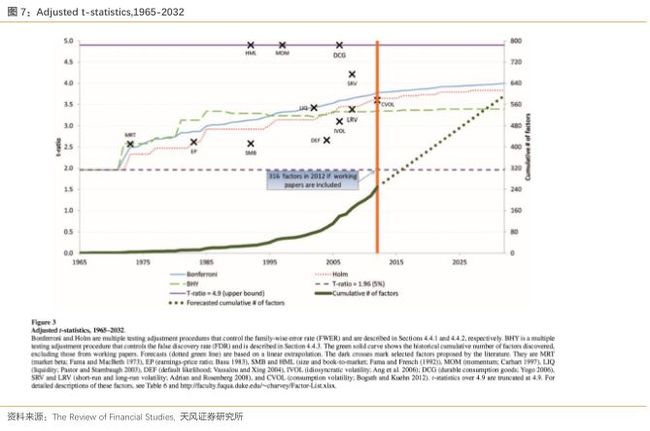
图2展示了被发现有效的因子数以及相关期刊数与年份之间的关系图。我们注意到过去十年间因子发掘速度的迅速增长。从1980年到1991年，每年几乎只有一个因子被发现，这个数字到1991到2003年期间增加到了5个，这激发了人们对于横截面上的收益率特点的研究兴趣，在过去的9年中，每年因子的发掘速度迅速增长到了18，总计164个因子被发掘。这个数字是之前年份里所有被发现的因子数量的2倍。

我们得到了316个被发现因子的t统计量，包括工作论文里的部分。这些t统计量绝大多数都超过了5%显著性水平的临界值1.96,。那些没达到临界值的都来自于那些提出了很多因子的论文。这些因子只代表了那些被检验过但t统计量没有达到临界值的因子中的很小一部分。

4、模型结果

4.1 假设所有检验都公开情况（M=R）下的p值校正

我们在假设所有被检验过的因子的检验结果我们都已知的情况下，应用之前介绍的三种校正方法。我们知道这样的假设是不真实的，因为我们低估了在传统的检验标准下不显著的因子的数量，我们会在后续设计处理这个数据缺失问题的方法。尽管有这些缺陷，我们在这一假设下得到的结果仍然至少在2个方面有意义。首先，基于我们的不完整样本得到的t统计量的临界值比真实的临界值要低，所以未来新因子的t统计量至少先超过我们的临界值才能被认为显著。其次，我们的结果可以在贝叶斯或者分层检验框架下进一步合理化。

基于我们样本中的那些已被公布因子的t统计量，我们可以得到t统计量的3种临界值。具体来说，在每一个时间点，我们把已得到的t统计量转化成相应的p值，然后应用上述的三种校正方法得到p值的三个临界值，最后再在t分布收敛于标准正态分布的假设下把这三个临界值在转化成相应的t统计量的临界值。为了指导将来的研究，我们还在假设因子发掘速度和2003-2012年间一样的基础上预测了在未来每年的t统计量临界值。

为了观察新的临界值如何更好地展现因子的统计显著性，图3中标出了一些因子的t统计量。其中，HML,MOM,DCG,SRV和MRT在三种校正方法下都依然显著，EP,LIQ,CVOL在部分校正方法下显著，而剩下的因子在各种校正下都不显著。

4.2 检验的稳定性

4.2.1 检验统计量间的相关性

有一个上述三种校正方法都需要考虑的问题，在多重检验中，如果数据之间存在一定的相关性，那么校正方法就会显得过于严格。在一个有相关性的数据中，这些方法会过多地惩罚第一类错误而使得第二类错误率增高。

理论上来说，在检验之间都独立的前提下，Bonferroni和Holm都能在检验数很多的情况下达到我们设定的显著性水平，但是，如果检验之间存在一定程度的相关性，这2个校正方法就会产生比我们希望的更少的阳性结果。也就是说，考虑一个极端情况，所有检验都一样的时候（所有的相关性都是1），我们根本就不需要进行多重检验，FWER和单假设检验的第一类错误率是一样的，所以通常用的单假设检验就足够了。类似地，BHY也会在检验之间存在相关关系时产生更少的阳性结果。

下面我们就需要讨论一些可能会违背我们假设的情形。首先，那些衡量同一种类型的风险的因子可能是相关的。如果这种相关性存在，就会导致在这三种校正方法下产生更少的阳性结果。其次，那些通过不同的样本去对同一个因子进行检验的研究也会产生高度相关的检验统计量，一个典型例子就是研究规模效应的一系列文章。所以我们通过尽可能只包含提出新因子的论文去减少这个问题。最后，如果检验统计量之间的相关性可以通过Pearson相关性检验被证实，我们在第五部分提出了一个新模型来系统性地将相关性的信息包含在内。

4.3 M>R的情形

为了解决M>R也就是存在没有被公布的检验的问题，我们在附录A中提出了一个仿真模型来估计临界t统计量。这个模型的主要思想是首先不考虑所有被尝试过的因子t统计量的潜在分布去产生t统计量的临界值，再使用三种校正方法去校正被模拟出的t统计量样本。

基于我们的估计，有71%被尝试过的因子被丢失。引入这个信息，Bonferroni和Holm方法的新的临界t统计量分别是4.01和3.96,都比M=R的时候要高，这是符合我们预期的。而BHY方法在1%和5%的显著水平下分别从3.39,2.78增加到了3.68,3.18。综合考虑上述各种情形，我们认为t统计量最小临界值是3.18，也就是M>R时BHY校正方法5%显著性水平下的临界值。

4.3.1 检验统计量之间的相关性

尽管BHY方法在检验统计量之间有任意相关性的情况下都有较好的稳定性，但是它并没有用到相关性的信息。当这些信息被恰当地包含在方法内时，可以使得方法更加准确。我们主要关注可以被Paerson相关性检验证实的相关性。在我们的研究中，检验统计量之间的相关性等价于因子收益率之间的相关性。

 

我们假设同一时期的两个因子的收益率的相关系数是ρ，不同时期的相关系数是0。最后，为了包含那些隐藏的检验，我们假设M个因子被检验，但只有达到一定的t统计量临界值的因子才被公布。我们设置这个临界值为1.96并关注被公布因子中t统计量大于1.96的因子的子集。但是，t统计量刚刚超过1.96的因子被公布的可能性比那些t统计量大的因子更低，所以我们拥有的的公布的因子的子集只包含了一部分检验中t统计量大于1.96，为了克服这个数据缺失问题，我们假设我们的子集包含了比例为r的t统计量在1.96到2.57之间的因子和所有t统计量大于2.57的因子。例如，r=1/2时，我们简单地复制t统计量在1.96到2.57之间的样本并保留t统计量大于2.57的所有样本来构建所有的样本。

其中w0和{wi},i=1,2,3是与平方距离相关的权重。通过广义矩量法（GMM），我们将这些权重设置为w0 =1和w1 = w2 = w3 = 10,000。我们估计模型中的三个参数（λ，p0和M），然后选择校准相关系数ρ。特别是，对于给定的相关性ρ，我们通过数值搜索最小化目标函数D（λ，p0，M，ρ）的模型参数（λ，p0，M）。

4.3.2 结果

综合在各个相关性水平的结果，我们估计分别需要3.9,3.0的临界值去控制FWER在5%和FDR在1%。注意到这个数字和我们之前的估计相差不大（Holm校正控制FWER在5%的临界值为3.78，BHY校正控制FDR在1%的临界值为3.38）。但是，这些相似的数字是在不同的机制下产生的。我们现在的估计是假设了因子收益率之间有一定的相关性并且假设有超过1300个因子检验。而我们之前的是假设316个公布的因子就是全部的因子并且认为没有相关性。

我们的样本无法对相关性水平作出直接的推断。但是，在表5中我们发现ρ取0.2时可以使得我们的优化目标函数取值最小，此外，我们分析了S%PCAPITAL IQ数据库中包含的美国股票市场超过400个因子的收益率时间序列数据，估计1985到2014年间的平均相关性为0.15，再结合相关文献的数据，我们最后相信因子收益率之间的平均相关性为0.2左右。

5、总结

至少316个因子被检验过以用来解释期望收益率的横截面，这些因子大部分都是在过去十年值提出。我们的论文提出将常规的统计显著性的临界值（例如t统计量超过2.0）用于资产定价是一个严重的错误。考虑到因子过剩和无法避免的数据挖掘，许多历史上被发现的因子只是因为偶然而被认定为了显著。

我们的方法中嵌入了一个重要的哲学问题。我们的临界值会随着时间而增加因为有更多的因子被数据挖掘出来，但是数据挖掘并不是新事物。为什么现在的数据挖掘要设置比1980年代的数据挖掘更高的阈值？我们认为，有三个原因用来解释为什么现在的标准更加严格。首先，“低处的水果已经被采摘了“，也就是说，发现真实有效因子的比率可能已经降低。其次，数据量有限。基于CRSP数据库只能做这么多事情。相反，在粒子物理学中，通常会在实验中创建数万亿个新观测值。我们在金融领域上没有那么奢侈。第三，数据挖掘的成本已大大降低。过去，数据收集和估计需要大量时间，因此，只有那些基于经济学原理的因子才有更高的优先级被用来检验，

我们的论文介绍了三种传统的多重检验的框架和一个尤其适合金融经济学研究的新框架。尽管这些框架假设不同，他们的结论是一致的。我们认为一个新发现的因子应该有超过3.0的临界值。我们还提供了一个推荐临界值的时间序列（从1967年到现在）。许多公布的因子没有达到我们的推荐临界值。

尽管3.0的临界值（对应p值0.27%）似乎是一个很高的标准，我们还有足够的理由认为3.0的标准太低了。首先，我们把选择了主流杂志上和一小部分工作论文里公布的因子。第二，一定有许多进行了实证检验但失败了没有公布的因子。事实上，未来的金融经济学研究一定是聚焦在发现新因子。考虑到我们只计算了316个因子，肯定太少了，这意味着t统计量的临界值有可能会更高。

那么3.0的临界值能用于未来每个新因子的检验吗，可能不能。来源于第一手的经济学原理的因子应该比完全来源于实证经验的因子有更低的阈值。但不管怎样，2,0的临界值即使是对纯来源于理论的因子也是不再合适的。

在医学研究领域，多重检验问题的提出导致他们发现许多公布的研究发现并不是真的，我们对因子的发掘也有同样的结论-许多在金融领域发现的因子其实有可能是假阳性：296个被公布的显著因子中，在Bonferonni校正下158个是假阳性，Holm下142个，BHY（1%显著水平）下132个，BHY（5%显著水平）下80个。此外，有这么多的因子也不符合主成分分析的原则。

具有讽刺意味的是，研究人员遵循的经典的统计学规则（例如，随机化，无偏）个人激励的概念背道而驰，而个人激励是经济学的基本前提之一。重要的是，数据挖掘的最佳数量不为零，因为一些数据挖掘的确产生了新的知识。正如Glaeser（2008）所说，关键是设计适当的统计方法来调整偏差。我们在文中详细阐述的多重检验框架就是与上述的建议符合的。

我们的研究量化了Fama（1991）和 Schwer（2003）提出的警告并且试图建立新的标准来指导资产定价的实证检验。

来源：量化先行者     作者：天风金工吴先兴团队

推荐阅读：

1.一个量化策略师的自白（好文强烈推荐）

2.市面上经典的量化交易策略都在这里了！（源码）

3.期货/股票数据大全查询（历史/实时/Tick/财务等）

4.干货| 量化金融经典理论、重要模型、发展简史大全

5.干货 | 量化选股策略模型大全

6.高频交易四大派系大揭