The Hidden Agenda User Simulation Model翻译

摘要

对语音对话系统采用统计方法的主要优势是能够将对话策略形式化设计为随机优化问题。但是，由于对话策略是通过交互式探索替代对话路径来学习的，因此常规的静态对话语料库不能直接用于训练，而改为使用用户模拟器。本文介绍了一种基于栈结构的表示形式（称为用户议程）的新的统计用户模型，该模型允许将状态转换建模为推入和弹出的操作序列，并从用户的角度优雅地对对话历史进行编码。提出了一种基于期望最大化的算法，该算法根据一系列隐藏状态对可观察到的用户输出进行建模，从而使模型可以在最少注释数据的语料库上进行训练。具有真实对话系统的实验结果表明，训练有素的用户模型可以成功地用于优化对话策略，该对话策略在任务完成率和用户满意度方面优于手工baseline。

1.介绍和总览

1.1 统计语音对话系统

　　传统语音对话系统（SDS）的一般体系结构如图1所示。语音识别器接收用户发出的声音信号$x_u$，将其转换为基于特征的表示形式，并输出最可能的单词序列${\tilde{w}}_u$。由语音识别器得到基于文本的输出，然后由语音理解组件进行语义解码，并与含义表示相关联，通常以对话行为${\tilde{a}}_u$的形式进行。在输出端，遵循相反的过程。机器生成的对话动作$a_m$被转换为单词$w_m$的序列，使用文本到语音的组件进行合成以产生声音输出信号$x_m$。
　　SDS核心部分的对话管理器（DM）的任务是控制对话的流程，处理由于语音识别和理解错误而引起的不确定性以及执行目标计划。DM会解释观察到（并可能已损坏）的用户行为${\tilde{a}}_u$，解析上下文引用，并更新计算机的内部状态$s_m$。基于$s_m$，然后根据系统的对话策略选择适当的系统响应$a_m$，该策略定义了机器的对话行为。

1.2 基于模拟的强化学习

　　由于对话策略是通过交互式探索替代对话路径来学习的，因此常规的静态对话语料库无法直接用于训练统计DM。取而代之的是使用两阶段方法（见图2）。在第一阶段，使用系统原型或绿野仙踪设置，在与真实用户收集的有限对话数据上训练用户行为的统计模型。在第二阶段，通过与模拟用户进行交互的强化学习来优化对话管理器。用户行为通常在对话行为的抽象级别上建模，因为这避免了生成的语音信号或单词序列的不必要的复杂性。如图2所示，还可以添加错误模型来模拟用户与系统之间的嘈杂的通信通道。基于模拟的方法允许进行任意次数的训练，从而使学习型DM可以详尽地探索可能策略的空间。
　　假设模拟用户很好地概括了未知的对话状况，那么它也使DM可以偏离训练语料库中存在的对话策略，从而有可能探索新的和可能更好的策略。

1.3 统计用户模型

在[7]中给出了用于对话优化的模拟用户技术的调查。构建良好的用户模拟器的许多困难在于，在保持较小且易于训练的模型参数集的同时，结合以现实方式再现用户行为复杂特征这一个矛盾的目标。 Levin和Pieraccini在语义级别的用户模拟方面的早期工作调查了使用简单的二元模型$P(a_u|a_m)$预测用户对机器行为的响应。尽管可以轻松地在数据上训练该模型的参数，但是生成的对话通常由于模拟用户不断更改其目标，具有重复信息或违反逻辑约束，而缺乏现实性。因此，以后的工作研究了使用明确的目标表示和较长的对话历史，以确保对话过程中用户行为的更大一致性。通常，需要某种用户状态$s_u\in S_u$表示来捕获相关对话历史记录并实现用户行为的一致性。可以在文献中找到各种不同的状态空间定义和用于$P(a_u|a_m)$建模的技术，包括基于特征丰富的信息状态的方法，聚类技术和隐马尔可夫模型。
　　训练基于状态的用户模型时出现的实际问题是，在人机对话数据中是无法观察到真实的用户状态$s_u$。在现有的基于状态的方法中，通常通过使用具有对话状态信息的标签训练数据并限制用户的输出为带注释的对话状态$s_d\in {\mathcal{S}}_d$而非未知的用户状态$s_u$上来规避此问题。尽管这简化了训练过程，但需要预先定义状态空间${\mathcal{S}}_d$并提供必要的注释，这需要大量的工作。（1）如果用手工来完成，则代价会很昂贵，并且可能难以确保注释者之间的一致。（2）使用自动工具进行对话状态注释可以提高效率，但是工具本身的开发是一个耗时的过程，如果不手动检查大量数据就无法评估自动注释的正确性。因此，非常需要一种新的模型参数估计方法，该方法仅需要如本文中提出的直接从可观测的用户话语中推导出对话行为即可。

1.4 论文大纲

本文介绍了一种基于用户状态的栈结构的表示概念的新型统计方法，用于用户模拟。这种待处理的对话结构被称为用户议程，是一种方便的机制，可用于编码对话历史记录和用户的“心理状态”（第二节）。为了允许在最小标注的训练数据上执行模型参数估计而没有特定于状态的注释，提出了一种基于期望最大化（EM）的算法，该算法根据一系列隐藏的议程状态对可观察到的用户输出进行建模（第三节） 。尽管可能的议程状态和状态转换的空间很大，但事实表明，通过减少对原子推入和弹出操作序列的动作选择和状态更新，可以实现可处理性。使用动态增长的树形结构表示状态序列以及用于状态转换的抽象空间映射，然后可以在最少注释的数据上成功执行参数估计。
　　本文大量关注评估方法和结果（第四至第六节）。在4.1节中概述了实验设置之后，4.2节中介绍了对话策略训练实验，4.3节中介绍了基于规则的对话管理器来作为baseline。第五节报告的基于模拟的结果表明，使用基于议程的用户模型训练的策略要优于使用baseline的模拟器训练的策略，并表明在嘈杂条件下进行训练的好处。通过对36个主题进行的用户研究表明，所学习策略的强大性能也可以延续到现实世界中的人机交互任务（第六节）。最后，第七节对论文进行了总结，并概述了未来的工作。

2.隐藏议程模拟用户模型

2.1 语义级别的用户行为

人机对话在语义层面上可以形式化为一系列状态和对话行为。对话行为大体上“代表了言外之意”。 它们使用户模型和对话管理器接口得以标准化，并成为标注对话数据的注释标准。对话行为分类法的定义是一个持续的研究领域，可以在文献[19] – [21]中找到各种不同的建议。
　　对于本文提出的实验，使用了剑桥大学工程系（CUED）对话动作数据集。CUED数据集非常紧凑，旨在涵盖建模简单的数据库检索任务所需的交互功能。与其他对话动作数据集相比，它的主要区别在于，它允许将语音解码或标记为替代对话动作的分布，从而避免了每个语音允许多个对话动作时出现的计算问题。为此，该方案使用动作类型定义，该定义允许将每个话语表示为单个动作，而不是动作的组合。通过使对话行为与概率相关联，可以用一组对话行为假设来标记每个话语，其概率总和为$1$。CUED对话动作数据集的语法要求每个动作的形式为：
$$acttype(\underset{actitems}{a=x,b=y,\cdots })\{prob\}$$
其中$prob$表示假设的概率。$acttype$指对话动作的类型，例如$inform(...),request(...)$或$hello(...)$。接下来参数列表（可能为空）$a=x,b=y$称为对话动作项。这些项通常是诸如$food=French$或$drinks=wine$之类的时段值对，但也可以是诸如$addr$之类的各个槽名称。例如，在稍后第四节中描述的旅游信息领域，话语$“IamlookingforacheapChineserestaurantneartheCinema”$将被编码为$inform(type=restaurant,pricerange=cheap,food=Chinese,near=Cinema)$，而$“CanyougivemetheaddressandphonenumberofPizzaPalace?”$将被编码为$request(addr,phone,name{=}^{\prime }PizzaPalac{e}^{\prime })$。速记符号$a_u[i]$将用于表示动作$a_u$和$\mathbb{T}(a_u)$表示$a_u$的$acttype$的第$i$个项目。

2.2 将状态分解为目标和议程

　　在任何时刻$t$，用户都处于状态$s_u\in {\mathcal{S}}_u$，执行操作$a_u\in {\mathcal{A}}_u$，转换为中间状态$s_u^{\prime }$，接收机器操作$a_m$，然后转换为下一个状态$s_u^{\prime \prime }$，并重新开始下一循环。请注意，在本文全文中，双破折号将用于表示时刻$t+1$的状态，因此：
$$s_u\to a_u\to s_u^{\prime }\to a_m\to s_u^{\prime \prime }\to ...\text{\hspace{1em}(1)}$$
　　假设采用马尔可夫状态表示，则可以将用户行为分解为三个模型：$P(a_u|s_u)$用于用户动作的选择，$P(s_u^{\prime }|a_u,s_u)$用于将状态转换为$s_u^{\prime }$，以及$P(s_u^{\prime \prime }|a_m,s_u^{\prime })$用于将状态转换为$s_u^{\prime \prime }$。受基于议程的对话管理方法的启发，用户状态$s_u$被分解为议程$A$和目标$G$，即$S=(A,G)$，其中$G=(C,R)$由约束$C$和请求$R$组成。在对话过程中，目标$G$以一致的，目标明确的方式确保用户行为。约束$C$指定所需的场所，例如$“acentrallylocatedbarservingbeer”$，而请求$R$指定所需的信息，例如$“thename,addressandphonenumberofthevenue.”$。$C$和$R$都可以方便地表示为【槽/值】对列表，如以下示例所示：
$$C=\left[\begin{array}{c}type=bar\\ drinks=beer\\ area=central\end{array}\right]R=\left[\begin{array}{c}name=\\ addr=\\ phone=\end{array}\right].$$
　　用户议程$A$是一个栈的结构，其中包含引发目标中指定的信息所需的用户对话操作。（1）在对话开始时，使用系统数据库随机生成一个新目标，并通过将所有目标约束转换为$inform()$行为并将所有目标请求转换为$request()$行为来填充议程。此外，在议程的底部添加了$bye()$动作以结束对话。因此，上面介绍的示例的初始议程A如下所示。（2）随着对话的进行，议程会动态更新，并且从议程的顶部选择行为以形成用户行为。在该示例中，通过从$A$弹出$n=2$个项以给出$A^{\prime }$来生成用户响应$a_u=inform(type=bar,drinks=beer)$，如下所示：

　　基于响应于得到的机器行为$a_m$，新的用户行为被推入到议程上，不再删除相关的行为。因此，议程是跟踪对话进度以及对相关对话历史进行编码的便捷方式。当需要首先发出较高优先级的动作时，也可以临时存储对话动作，从而为模拟器提供了简单的用户存储模型（详细说明请参见图3）。相比之下，当使用基于n元语法的方法时，除非将n设置为一个较大的值，否则将忽略对话轮次之间的这种长距离依赖性，这反过来通常会导致泛化较差和模型参数估计不可靠。
　　基于议程的方法的另一个（也许不太明显）优点是，当对话因识别错误而损坏或传入的系统动作与当前任务无关时，它使模拟用户可以主动采取行动。后一点对于训练统计对话管理模型至关重要，因为通常是从随机开始学习策略。早期训练阶段的“对话历史”通常是一系列随机对话行为或对话状态，在训练数据中从未见过。在这种情况下，即使在系统看起来毫无目标的情况下，对话栈仍可在议程上起作用，从而使用户模型能够主动采取行动并以目标导向的方式行事。

2.3 动作选择和状态转移模型

将用户状态$s_u$分解为目标$G$和议程$A$简化了动作选择和状态转换的模型。
　　（1）动作选择模型
　　假定议程（长度为$N$）是根据优先级排序的，其中$A[N]$表示顶部，$A[1]$表示底部。因此，形成用户响应等同于从堆栈顶部弹出$n$个项。假设$a_u[i]$表示$a_u$中的第$i$个对话行为，则最终用户行为如下所示：
$$a_u[i]:=A[N-n+i]\forall i\in [1\dots n],1\le n\le N.\text{\hspace{1em}(2)}$$
　　使用$A[N-n+1\dots N]$作为$A$上前$n$个项的简写，则动作选择模型变为：
$$P(a_u|s_u)=\delta (a_u,A[N-n+1\dots N])P(n|A,G)\text{\hspace{1em}(3)}$$
其中Kronecker delta函数$\delta (p,q)$表示如果$p=q$则为1，否则为零。这意味着，如果可以从$A$弹出$a_u$，则只能在状态$s_u=(A,G)$中生成用户响应$a_u$。相应弹出操作的概率取决于弹出项的数量$n$，并且以$A$和$G$为条件。
　　（2）状态转移模型
　　状态转换模型$P(s_u^{\prime }|a_u,s_u)$和$P(s_u^{\prime \prime }|a_m,s_u^{\prime })$被重写如下。在弹出$a_u$并使用$N^{\prime }=N-n$表示$A^{\prime }$的大小之后，令$A^{\prime }$表示议程，我们有：
$$A^{\prime }[i]:=A[i]\forall i\in [1\dots N^{\prime }]\text{\hspace{1em}(4)}$$
　　使用$A^{\prime }$的这种定义并假设目标在用户执行$a_u$时保持不变，则由$a_u$决定的第一个状态转换是完全确定性的，因为它仅涉及从议程中弹出给定数量的项：
$$P(s_u^{\prime }|a_u,s_u)=P(A^{\prime },G^{\prime }|a_u,A,G)=\delta (A^{\prime },A[1\dots N^{\prime }])\delta (G^{\prime },G).\text{\hspace{1em}(5)}$$
　　基于$a_m$的第二个状态转换被分解为目标更新和议程更新步骤：
$$P(s_u^{\prime \prime }|a_m,s_u^{\prime })=\underset{agendaupdate}{P(A^{\prime \prime }|a_m,A^{\prime },G^{\prime \prime })}\underset{goalupdate}{P(G^{\prime \prime }|a_m,G^{\prime })}\text{\hspace{1em}(6)}$$
　　（3）模型参数
　　现在可以将模型参数集合$\theta$总结为：
$$\theta =\{P(n|A,G),P(A^{\prime \prime }|a_m,A^{\prime },G^{\prime \prime }),P(G^{\prime \prime }|a_m,G^{\prime })\}.\text{\hspace{1em}(7)}$$
以下各节将讨论公式(6)中的RHS上显示的更新步骤。

3.模型参数估计

3.1 将用户状态作为隐藏变量

估计动作选择和状态转移模型的参数并非易事，因为在训练数据中无法观察到由目标和议程表示的状态。如本文第一节所述，先前基于状态的统计用户模拟方法的工作通过用对话状态信息来标记训练数据来规避无法观察到的用户状态问题，并根据观察到的对话状态调节用户输出。虽然这简化了训练过程，但提供需要的注释容易出错，并且需要大量的精力。
　　这里提出的参数估计方法通过议程和用户目标状态的隐藏序列对可观察到的用户和机器对话行为进行建模，从而避免了对话状态注释的需要。更正式地说，每个对话数据$D$包含$T$轮对话：
$$\mathcal{D}=\{{\text{a}}_u,{\text{a}}_m\}=\{a_{m,1},a_{u,1},...,a_{m,T},a_{u,T}\}\text{\hspace{1em}(8)}$$
用隐藏变量$X=\{\text{A},\text{G}\}$建模，其中$\text{A}=\{A_1,A_1^{\prime },...,A_T,A_T^{\prime }\}$和$\text{G}=\{G_1,G_1^{\prime },...,G_T,G_T^{\prime }\}$。从第二节收集的结果，注意到从式(5)中选择$n$个确定性固定的$A^{\prime }$，并用$A_t^{\prime \prime }$表示$A_{t+1}$，联合概率可以表示为：
$$\begin{gathered} P(X,\mathcal{D})=\prod _{t=1}^{T-1}P(n_t|A_t,G_t) \\ \times P(A_t^{\prime \prime }|a_{m,t},A_t^{\prime },G_t^{\prime \prime })P(G_t^{\prime \prime }|a_{m,t},G_t^{\prime })P(a_{m,t}).\text{\hspace{1em}(9)} \end{gathered}$$
　　目标是学习模型参数$\theta$的最大似然（ML）值，以使对数似然$\mathcal{L}(\theta )=logP(\mathcal{D}|\theta )$最大化：
$$\begin{gathered} {\theta }_{ML}=\underset{\theta }{\mathrm{argmax}}\mathcal{L}(\theta )=\underset{\theta }{\mathrm{argmax}}logP(\mathcal{D}|\theta ) \\ =\underset{\theta }{\mathrm{argmax}}log\sum _{X}P(X,\mathcal{D}|\theta ).\text{\hspace{1em}(10)} \end{gathered}$$
　　由于在(10)中存在隐藏变量之和，因此$\mathcal{L}(\theta )$的直接优化是不可能的，但是，可以使用基于迭代期望最大化（EM）的方法来找到隐藏变量模型似然的（局部）最大值。 如[25]所示，这涉及到最大化辅助函数：
$$Q(\theta ,{\theta }^{(k-1)})=\sum _X(X,\mathcal{D}|{\theta }^{(k-1)})logP(X,\mathcal{D}|\theta ).\text{\hspace{1em}(11)}$$
并导出(12)–(14)中给出的参数重新估计公式：

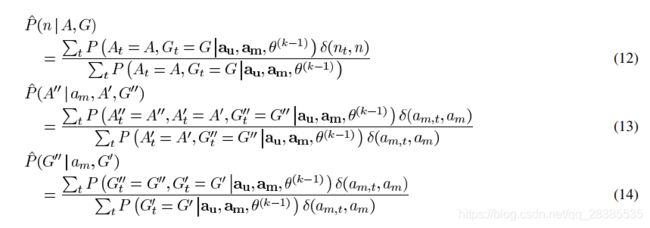
3.2 将议程作为一系列推入动作来更新

以易处理的方式实现上述隐藏变量方法并非易事。用于本文所提出的实验的用户和机器对话动作集${\mathcal{A}}_u$和${\mathcal{A}}_m$的大小为$|{\mathcal{A}}_u|\approx 10^3$和$|{\mathcal{A}}_m|\approx 10^3$。使用先前SDS用户试验中使用的目标规范的典型值，目标状态空间的大小可以估算为$|\mathcal{G}|\approx 10^7$。议程状态空间$\mathcal{A}$的大小取决于上文所定义的用户对话动作$|{\mathcal{A}}_u|$的数量以及在议程上的用户对话动的最大数量。议程的最大长度是可选择的设计，但是除非设置为至少8，否则很难模拟现实的对话。如[25]所示，$\mathcal{A}$包含大量的$|\mathcal{A}|\approx 10^{20}$个潜在议程状态，因此模型$P(A^{\prime \prime }|a_m,A^{\prime },G^{\prime \prime })$所需的参数数量约为：
$$|\mathcal{A}\times {\mathcal{A}}_m\times \mathcal{A}\times \mathcal{G}|\approx 10^{50}\text{\hspace{1em}(15)}$$
　　这些估计表明，当不对${\mathcal{A}}^{\prime \prime }$施加任何限制时，从${\mathcal{A}}^{\prime }$到${\mathcal{A}}^{\prime \prime }$的可能状态转换的空间是非常大的。尽管以上给出的数字是此处展示的特定于议程模型和对话领域的估计，但是任何假定真实状态为隐藏状态的用户模型训练算法都可能出现类似的易处理性问题，无论状态表示如何。基于议程的状态表示形式具有显著优势，可以假定每个状态都从先前的状态派生而来，并且每个转移只需要有限数量的明确定义的原子操作。如本节其余部分所示，这可以在不过度限制模型的表达能力的情况下实现易处理性。
　　（1）更具体地说，议程从${\mathcal{A}}^{\prime }$转移到${\mathcal{A}}^{\prime \prime }$可以看作是将一系列对话行为添加到议程顶部的推入式操作。在第二个“清理”步骤中，必须删除重复的对话动作、“空”动作和对于已经填充的目标请求槽的不必要的$request()$动作，但这是确定性的过程，因此为了简化起见，可以将其排除在以下推导中 。仅考虑推入操作，议程底部的项从$1$到$N^{\prime }$保持不变，并且议程更新模型可以重写如下：
$$\begin{gathered} P(A^{\prime \prime }|a_m,A^{\prime },G^{\prime \prime }) \\ =P(A^{\prime \prime }[1..N^{\prime }],A^{\prime \prime }[N^{\prime }+1..N^{\prime \prime }]|a_m,A^{\prime }[1..N^{\prime }],G^{\prime \prime }) \\ =\delta (A^{\prime \prime }[1..N^{\prime }],A^{\prime }[1..N^{\prime }])\times P(A^{\prime \prime }[N^{\prime }+1..N^{\prime \prime }]|a_m,G^{\prime \prime })\text{\hspace{1em}(16)} \end{gathered}$$
　　（2）现在可以通过假设$a_m$中的每个对话行为（槽值对）触发一个推入操作来进一步简化（16）的RHS的第二项。可以进行这种假设而不会失去一般性，因为推入“空”行为（以后将其删除）或推入一项以上的行为是可能的。这种假设的优势在于，$a_m$中已知的项数目$M$决定了推入操作的次数。因此，$N^{\prime \prime }=N^{\prime }+M$，并且：
$$\begin{gathered} P(A^{\prime \prime }[N^{\prime }+1..N^{\prime \prime }]|a_m,G^{\prime \prime }) \\ =P(A^{\prime \prime }[N^{\prime }+1..N^{\prime }+M]|a_m[1..M],G^{\prime \prime })(17) \\ =\prod _{i=1}^{M}P(A^{\prime \prime }[N^{\prime }+i]|a_m[i],G^{\prime \prime })\text{\hspace{1em}(18)} \end{gathered}$$
　　表达式(18)表明，系统动作中的每个项$a_n[i]$都会触发一个推入操作，并且该操作取决于目标。例如，假设$a_m[i]$中的项$x=y$违反了$G^{\prime \prime }$中的约束，则可以将以下之一推到$A^{\prime \prime }$中：$negate()$，$inform(x=z)$，$deny(x=y,x=z)$等。
　　令$a_{push}\in {\mathcal{A}}_u$表示推入动作$A^{\prime \prime }[N^{\prime }+i]$，$a_{cond}\in A_m$表示包含单个对话动作项$a_m[i]$的条件对话动作。在式(16)中省略Kronecker delta函数，议程更新步骤随后减少为重复应用推入转换模型$P(a_{push}|a_{cond},G^{\prime \prime })$。模型$P(a_{push}|a_{cond},G^{\prime \prime })$所需的参数数量约为：
$$|{\mathcal{A}}_u\times {\mathcal{A}}_m\times \mathcal{G}|\approx 10^{13}\text{\hspace{1em}(19)}$$
尽管数量仍然很大，但这个数量要比建模从$A^{\prime }$到$A^{\prime \prime }$的无限制转移所需的参数数量小得多。

3.3 推入转移的简易空间模型

　　（1）为了进一步减小模型参数的大小并实现对$P(a_{push}|a_{cond},G^{\prime \prime })$的易于估计，引入“简易空间”的概念很有用，就像先前在对话管理的背景下所做的那样。首先，定义一个函数$\varphi$，用于将机器对话行为$a_{cond}\in {\mathcal{A}}_m$和目标状态$G^{\prime \prime }\in \mathcal{G}$从机器行为${\mathcal{A}}_m$和目标状态$\mathcal{G}$的空间映射到“简易条件”的较小简易空间${\mathcal{Z}}_{cond}$，如下所示：
$$\varphi :{\mathcal{A}}_m\times \mathcal{G}\mapsto {\mathcal{Z}}_{cond}with|{\mathcal{A}}_m\times \mathcal{G}|\gg |{\mathcal{Z}}_{cond}|.\text{\hspace{1em}(20)}$$
例如，所有尝试对违反现有用户目标约束$a=y$的槽值对$a=x$进行$confirm()$的系统动作$a_m$都映射到简易条件$ReceiveConfirmAXnotOk[a=x]$。
　　（2）其次，定义了“简易推入动作”空间${\mathcal{Z}}_{push}$，该空间将真实用户对话动作分组为较小的一组等效类。使用函数$\omega$，简易推入动作被映射回“真实”对话动作：
$$\omega :{\mathcal{Z}}_{push}\mapsto {\mathcal{A}}_{u}with|{\mathcal{Z}}_{push}|\ll |{\mathcal{A}}_u|.\text{\hspace{1em}(21)}$$
例如，简易推入动作$PushNegateAY$映射到实际的对话动作$negate(a=y){(}^{\prime \prime }No,Iwanta=y{!}^{\prime \prime })$。请注意，映射$\varphi$和$\omega$都是确定性的，需要由系统设计人员手工制作，这将在下面更详细地讨论。
　　（3）令$z_{push}\in {\mathcal{Z}}_{push}$和$z_{cond}\in {\mathcal{Z}}_{cond}$，议程状态转换模型可以在简易空间中定义为：
$$P(a_{push}|a_{cond},G^{\prime \prime })\approx P(z_{push|z_{cond}})\text{\hspace{1em}(22)}$$
其中$z_{cond}=\varphi (a_{cond},G^{\prime \prime })$和$a_{push}=\omega (z_{push})$。对于本文中介绍的实验，大约定义了30个简易条件和30个简易推入动作（请参见下面的示例和讨论）。因此，对议程状态转换进行建模所需的参数$P(z_{push}|z_{cond})$的总数为$|{\mathcal{Z}}_{cond}\times {\mathcal{Z}}_{push}|\approx 900$，即足够小从而可以根据实际对话数据进行估算。
　　（4）图4给出了简化示例，其给出了用于议程更新的简要空间技术。在该示例中，输入的机器动作$a_m=confreq(p=q,r)$是对槽值对$p＝q$的隐式确认和对槽$r$的请求。更新步骤如下进行：

• 根据目标的当前状态（此处未显示），第一步是将每个对话行为项（槽值对）映射到简易条件$z_{cond}$。假设示例中的确认$p=q$不违反任何用户目标中的约束条件，将其映射到$ReceiveConfirmAXok[p=q]$。对$r$的请求映射到$ReceiveRequestA[r]$。
• 现在为每个简易条件$z_{cond}$生成一个简易推入动作$z_{push}$的列表，每个动作的概率为$P(z_{push}|z_{cond})$。图中显示了一个（简短的）示例列表。例如，简易推入动作$PushInformAX$意味着将带有请求的槽（在这种情况下为$r$）的$inform()$动作推入到议程上。请注意，此时可以丢弃概率为零的简易推入操作。
• 现在，简易推入操作已映射到实际推入操作。这是大多数简易推入操作的一对一映射，但是某些简易推入操作可以映射到多个实际推入操作。在图中对简易推入操作$PushInformBY$进行了说明，这表示相应的实际推入操作是一个$inform()$对话操作，其中包含一些槽值对$B=Y$（而不是请求的槽），在这种情况下为$s=y$或$t=z$。在这种情况下，概率值在简易推入操作所对应的实际推入操作之间平均分配，如图所示。
• 现在使用每个简易条件中的一个实际推入动作，生成推入动作所有可能组合的列表。每个组合代表一系列将被推到议程上的对话行为。如图所示，每种组合都用于创建新议程。转换概率计算为用于进行转换的实际推入动作的乘积。

简易条件集${\mathcal{Z}}_{cond}$和简易推入操作集${\mathcal{Z}}_{push}$与领域无关，并且与槽和数据库条目的数量无关，因此允许将该方法扩展到更复杂的问题领域和更大的数据库上。${\mathcal{Z}}_{cond}$和${\mathcal{Z}}_{push}$的定义以及手工构建的映射函数$\varphi :{\mathcal{A}}_m\times \mathcal{G}\mapsto {\mathcal{Z}}_{cond}$和$\omega :{\mathcal{Z}}_{push}\mapsto {\mathcal{A}}_u$的实现需要详细了解对话行为集，并需要在槽填充对话场景中基本熟悉用户行为。但是，手工构建的映射函数不依赖于特定的领域和应用场景，而仅依赖于通用的应用类。
　　通过为每种机器对话行为类型定义一个简易条件，可以采用一种系统化的设计过程方法，例如，$ReceiveHello$用于$hello()$，$ReceiveInformAX$用于$inform(a=x)$，$ReceiveConfirmAX$用于$confirm(a=x)$。类似地，为每种用户行为类型定义了一个简易推入操作，例如，用于$hello()$的$PushHello$，用于$request(a)$的$PushRequestA$，用于$bye()$的$PushBye$。这确保了简易条件集覆盖了所有可能的机器对话行为和目标状态的空间，并且确保简易推入动作集覆盖了所有可能的用户对话行为的空间。对于第2.1节和[29]中所述的CUED对话动作集，这将导致一组大约15个简易条件和15个简易推入动作。然后可以通过“拆分简易条件”进一步细化${\mathcal{Z}}_{cond}$：例如，可以将$ReceiveConfirmAX$拆分为$ReceiveConfirmAXok$和$ReceiveConfirmAXnotOk$，以区分给定的槽值对$a=x$是否匹配或违反了现有用户目标约束中的槽$a$。类似地，可以通过选择一组更细粒度的简易推入操作来完善${\mathcal{Z}}_{push}$：例如，可以将$PushRequestA$拆分为$PushRequestForUnknownSlotA$和$PushRequestForFilledSlotA$。此过程通常需要反复试验，但是与使用状态特定信息注释对话语料库所涉及的工作相比，进行这些迭代改进所需的时间仍然微不足道。而且，结果可以在具有相同对话动作集的一类槽填充应用中重复使用。

3.4 议程状态序列表示

　　考虑到议程状态空间规模巨大，事先将所有状态直接枚举显然是行不通的。但是，对特定对话行为序列进行建模所需的实际状态数量要少得多，因为议程转换仅限于推入/弹出操作且取决于对话上下文。训练算法可以通过动态生成状态序列并丢弃任何$P(X,\mathcal{D}|\theta )=0$的状态序列$X$来利用这一点。
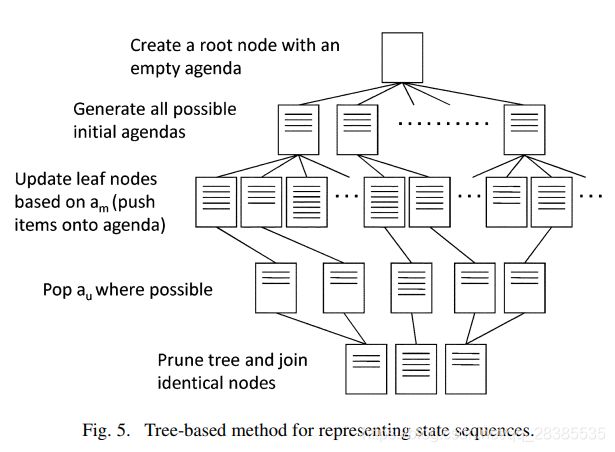
　　可以通过动态增长的树的形式找到适合的实现方式，该树可以将议程状态表示为树节点，而状态转换则表示为分支。通过创建包含空议程的根节点来初始化树，然后根据目标规范（如2.2节中所述）填充议程。由于对话在议程上的初始顺序是未知的，因此必须创建约束和请求的所有排列，如图5所示。
　　（1）初始化树后，通过生长树并为所有可能的状态序列创建分支来“解析”对话。基于机器对话动作$a_m$的更新涉及使用函数$\varphi$将$a_m$中的每个项映射到其对应的简易条件$z_{cond}$。并且对于每一个$z_{cond}$生成对应的简易推入操作$z_{push}$列表，并丢弃其中$P(z_{push}|z_{cond})=0$的项，然后使用$\omega$将简易推入操作映射回实际的推入操作，并用于创建新议程，这些议程作为新分支附加到树上。转移（分支）的概率计算为实际推动入动作概率的乘积（参见3.3节中的图4）。然后，以确定性的过程清理叶节点，以删除空的和重复的对话行为，删除$bye()$行为之下的所有对话行为，并删除对用户目标中已填写项的所有请求。
　　（2）在下一步中，将根据观察到的用户动作$a_u$更新树。此部分简化为在可能的情况下从议程顶部弹出$a_u$。不允许弹出$a_u$的议程表示状态的概率为零，可以将其丢弃。在所有其他情况下，具有更新议程的新节点将附加到树上。该分支被标记为弹出转移，并且根据弹出的项数计算其概率。
　　（3）基于$a_u$的更新完成后，将修剪树以减少节点和分支的数量。首先，删除在新一轮对话时未扩展的所有分支，即无法从叶节点议程弹出$a_u$的分支。剩下的所有分支代表议程状态的可能序列，到目前为止，对话行为的概率不为零。在第二步中，可以通过删除不具有给定最小叶节点概率的所有分支来执行更具侵略性的修剪类型。修剪后，通过合并具有相同议程的节点来进一步减小树的大小。
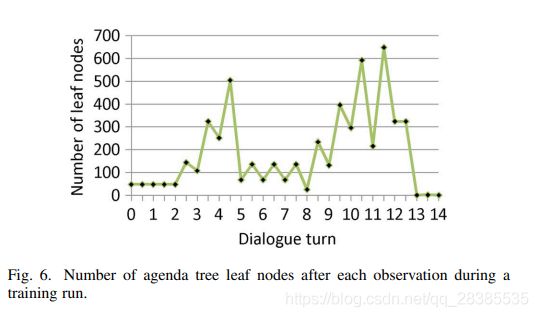
　　图6显示了样例对话的典型训练期间议程树叶子节点的数量。如上所述，对于每个机器对话动作，树被扩展，并且树每个分支上附加了一个或多个新节点，从而叶节点的数量保持恒定或增加。然后在可能的情况下执行弹出操作，修剪树并将相同的节点合并，以使数目保持不变或减少。对话结束时，仅剩下一个空议程的叶子节点。

3.5 动作选择和目标更新模型

动作选择和目标更新模型与议程更新模型一样遇到类似的易处理性问题，但是对于这两个模型，都发现了一种简单的解决方案可以产生令人满意的结果。
　　（1）动作选择模型
　　为了简化动作选择模型$P(n|A,G)$，可以将随机变量$n$设置为议程栈中最上层项的对话行为类型。令$\mathbb{T}(\cdot )$代表对话行为的类型，可以表示为：
$$P(n|A,G)=P(n|T(A[N])).\text{\hspace{1em}(23)}$$
　　然后，通过获取每个用户动作中对话行为项的频率次数，可以直接从对话数据中估计$n$个小整数值（通常在0到6范围内）上的概率分布$P(n|T(A[N]))$。
　　（2）目标更新模型
　　目标更新模型$P(G^{\prime \prime }|a_m,G^{\prime })$被分解为约束和请求的单独更新步骤。给定$C^{\prime \prime }$后，假设$R^{\prime \prime }$在条件上独立于$C^{\prime }$，则很容易证明：
$$P(G^{\prime \prime }|a_m,G^{\prime })=P(R^{\prime \prime }|a_m,R^{\prime },C^{\prime \prime })P(C^{\prime \prime }|a_m,R^{\prime },C^{\prime }).\text{\hspace{1em}(24)}$$
　　这两个更新步骤可以分别处理，并可以使用两个规则确定性地实现。1）如果$R^{\prime }$包含一个空槽$u$并且$a_m$是$inform(u=v,r=s,...)$形式的对话行为，并假定$a_m$中没有其他信息违反$C^{\prime \prime }$中的任何约束，则通过设置$u=v$从$R^{\prime }$转移到$R^{\prime \prime }$。 2）如果$a_m$包含对插槽$x$的请求，则将新约束$x=y$或$x=dontcare$添加到$C^{\prime }$中以形成$C^{\prime \prime }$。注意，这并不意味着用户必须对任何槽$x$的系统请求作出响应，因为议程更新模型不强制执行要发出的相应用户对话动作。
　　此处实现的目标更新模型实现允许用户在对话过程中更改目标，但将可能的目标状态转换的空间限制为确定性更新。这可以简化模型参数估计，因为可以从可观察到的对话行为顺序中直接推断出目标状态的顺序。但是，它将用户模拟器限制为用户不放松或修改其约束的对话任务。实际用户在所需场所不存在的情况下的行为，例如，不能始终被当前实现所覆盖。确定性更新模型也不是可训练的，这意味着无法从数据中学习不同目标状态转换的可能性。

3.6 应用前向/后向算法

通过将简易空间映射用于议程转换并简化上述目标更新和动作选择模型的假设，由(12)–(14)定义的参数更新方程集可简化为一个方程式：

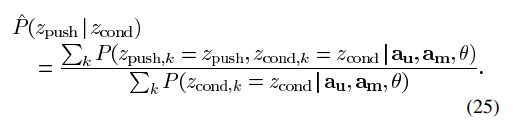
请注意，此处使用$k$而不是$t$，因为每个对话回合$t$都涉及两个状态转换，因此有$K=2T$个观察和更新步骤。现在可以通过应用前向/后向算法来有效地实现参数更新方程，如[25]所示。