n皇后2种解题思路与代码-Java与C++实现
林炳文Evankaka原创作品。转载请注明出处http://blog.csdn.net/evankaka
摘要:本文主要讲了n皇后问题的解题思路,并分别用java和c++实现了过程,最后,对于算法改进,使用了位运算。
一、问题抛出与初步解题思路
问题描述:八皇后问题是一个以国际象棋为背景的问题:如何能够在 8×8 的国际象棋棋盘上放置八个皇后,使得任何一个皇后都无法直接吃掉其他的皇后?为了达到此目的,任两个皇后都不能处于同一条横行、纵行或斜线上。
转化规则:其实八皇后问题可以推广为更一般的n皇后摆放问题:这时棋盘的大小变为n×n,而皇后个数也变成n。当且仅当 n = 1 或 n ≥ 4 时问题有解。令一个一位数组a[n]保存所得解,其中a[i] 表示把第i个皇后放在第i行的列数(注意i的值都是从0开始计算的),下面就八皇后问题做一个简单的从规则到问题提取过程。
(2)所有的皇后都不能在对角线上,那么该如何检测两个皇后是否在同一个对角线上?我们将棋盘的方格成一个二维数组,如下: 假设有两个皇后被放置在(i,j)和(k,l)的位置上,明显,当且仅当|i-k|=|j-l| 时,两个皇后才在同一条对角线上。
二、代码与结果
(1)C++版本
运行平台:VS2013
操作系统:Windows7
/**
* n皇后问题解决
* @author lin
*
*/
#include
#include
#include
using namespace std;
/**皇后的数目*/
static int num;
/**下标i表示第几行,x[i]表示第i行皇后的位置,注意此处0行不用*/
static int *x;
/**解的数目*/
static int sum = 0;
/**
* 判断第k行皇后可以放置的位置
* @param k k表示第k行,X[K]k表示第k行上皇后的位置
* @return boolean false表示此处不能放置皇后
*/
bool place( int k )
{
for ( int j = 1; j < k; j++ )
{
/* 如果当前传入的第K行上的皇后放置的位置和其它皇后一个对角线(abs(x[k]- x[j])==abs(k-j)或一个直线上(x[j] == x[k]) */
if ( abs( x[k] - x[j] ) == abs( k - j ) || x[j] == x[k] )
{
return(false);
}
}
return(true);
}
/**
* 一行一行的确定该行的皇后位置
* @param t
*/
void backtrack( int t )
{
if ( t > num ) /* 如果当前行大于皇后数目,表示找到解了 */
{
sum++;
/* 依次打印本次解皇后的位置 */
for ( int m = 1; m <= num; m++ )
{
//cout << x[m]; /* 这一行用输出当递归到叶节点的时候,一个可行解 */
//这里只是为了好看才写成下面的
for(int k =1; k <= num;k++){
if(k == x[m]){
cout << x[m] <<" ";
}else {
cout << "* ";//用*表示没有被用到的位置
}
}
cout << endl;
}
cout << endl;
} else {
for ( int i = 1; i <= num; i++ )
{
x[t] = i; /* 第t行上皇放在i列处 */
if ( place( t ) )
{
/* 此处的place函数用来进行我们上面所说的条件的判断,如果成立,进入下一级递归 */
backtrack( t + 1 );
}
}
}
}
int main()
{
cout<<"请输入皇后数目:";
cin>>num;
clock_t start,finish;
double totaltime;//计算程序运行时间
start=clock();//起始时间
x = new int[num + 1]; /* 此处注意加1,这里0行不用,1-num分别对应1-num行 */
for ( int i = 0; i <= num; i++ )
x[i] = 0;
backtrack( 1 ); /*传入第一个皇后,开始递归 */
cout << "方案共有" << sum;
delete[]x;
finish=clock();//结束时间
totaltime=(double)(finish-start)/CLOCKS_PER_SEC;
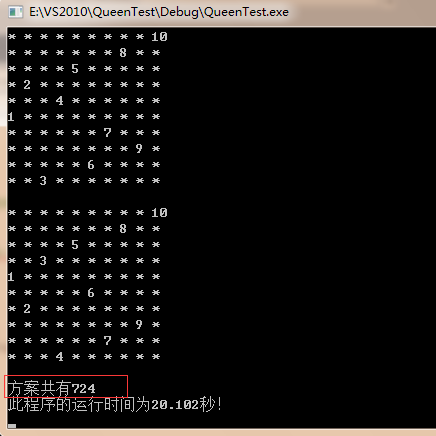
cout<<"\n此程序的运行时间为"< 输出结果:
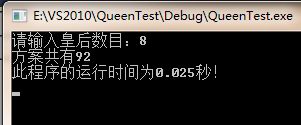
8皇后:
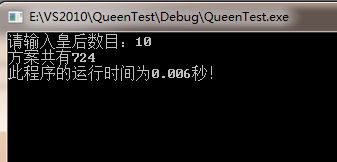
10皇后:
(2)java版本
运行平台:eclispse luna
操作系统:Windows7
package com.lin;
import java.lang.*;
/**
* n皇后问题解决
* @author lin
*
*/
public class QueenTest {
/**下标i表示第几行,x[i]表示第i行皇后的位置,注意此处0行不用*/
public int[] x;
/**皇后的数目*/
public int queenNum;
/**解的数目*/
public int methodNum;
QueenTest(int queenNum) {
this.queenNum = queenNum;
this.x = new int[queenNum+1];//注意,这里我们从第1行开始算起,第0行不用
backtrack(1);//从第一个皇后开始递归
}
/**
* 一行一行的确定该行的皇后位置
* @param t
*/
public void backtrack(int t)
{
if( t > queenNum) //如果当前行大于皇后数目,表示找到解了
{
methodNum++;//sum为所有的可行的解
//依次打印本次解皇后的位置
for(int m = 1; m <= queenNum; m++){
//System.out.println(x[m]);//这一行用输出当递归到叶节点的时候,一个可行解
//这里只是为了好看才写成下面的
for(int k =1; k <= queenNum;k++){
if(k == x[m]){
System.out.print(x[m]+" ");
}else {
System.out.print("* ");//用*表示没有被用到的位置
}
}
System.out.println();
}
System.out.println();
}
else{
for(int i = 1;i <= queenNum;i++)
{
x[t] = i;//第t行上皇后的位置只能是1-queenNum
if(place(t)) {//此处的place函数用来进行我们上面所说的条件的判断,如果成立,进入下一级递归,即放置下一个皇后
backtrack(t+1);
}
}
}
}
/**
* 判断第k行皇后可以放置的位置
* @param k k表示第k行,X[K]k表示第k行上皇后的位置
* @return boolean false表示此处不能放置皇后
*/
public boolean place(int k) {
for (int j = 1; j < k; j++)
// 如果当前传入的第K行上的皇后放置的位置和其它皇后一个对角线(abs(x[k]- x[j])==abs(k-j)或一个直线上(x[j] == x[k])
if (Math.abs(x[k] - x[j]) == Math.abs(k - j) || (x[j] == x[k])){
return false;
}
return true;
}
public static void main(String[] args) {
QueenTest queenTest = new QueenTest(8);
System.out.println("总共解数为:"+ queenTest.methodNum);
}
}
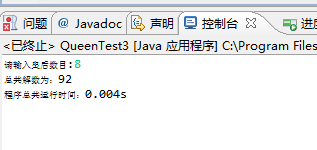
输出结果:
这是八皇后
三、更加高效的算法-位运算版本
上面的方法递归次数实在太多了,也浪费空间,下面介绍目前号称是最快的--位运算。原理就不介绍了,看这里吧http://blog.csdn.net/xadillax/article/details/6512318
(1)Java代码
package com.lin;
import java.util.Scanner;
/**
* n皇后问题解决
* @author lin
*
*/
public class QueenTest3 {
/**sum用来记录皇后放置成功的不同布局数*/
public long sum = 0;
/**upperlim用来标记所有列都已经放置好了皇后*/
public long upperlim = 1;
/**
* 试探算法从最右边的列开始。
* @param row 竖列
* @param ld 左对角线
* @param rd 右对角线
*/
void queenPos(long row, long ld, long rd)
{
if (row != upperlim)
{
// row,ld,rd进行“或”运算,求得所有可以放置皇后的列,对应位为0,
// 然后再取反后“与”上全1的数,来求得当前所有可以放置皇后的位置,对应列改为1
// 也就是求取当前哪些列可以放置皇后
long pos = upperlim & ~(row | ld | rd);
while (pos != 0) // 0 -- 皇后没有地方可放,回溯
{
// 拷贝pos最右边为1的bit,其余bit置0
// 也就是取得可以放皇后的最右边的列
long p = pos & -pos;
// 将pos最右边为1的bit清零
// 也就是为获取下一次的最右可用列使用做准备,
// 程序将来会回溯到这个位置继续试探
pos -= p;
// row + p,将当前列置1,表示记录这次皇后放置的列。
// (ld + p) << 1,标记当前皇后左边相邻的列不允许下一个皇后放置。
// (ld + p) >> 1,标记当前皇后右边相邻的列不允许下一个皇后放置。
// 此处的移位操作实际上是记录对角线上的限制,只是因为问题都化归
// 到一行网格上来解决,所以表示为列的限制就可以了。显然,随着移位
// 在每次选择列之前进行,原来N×N网格中某个已放置的皇后针对其对角线
// 上产生的限制都被记录下来了
queenPos(row + p, (ld + p) << 1, (rd + p) >> 1);
}
}
else
{
// row的所有位都为1,即找到了一个成功的布局,回溯
sum++;
}
}
/**
* 根据传入的皇后数目开始计算
* @param n 皇后数据
*/
void queen(int queenNum) {
if ((queenNum < 1) || (queenNum > 32)) {
System.out.println(" 只能计算1-32之间\n");
return;
}
// N个皇后只需N位存储,N列中某列有皇后则对应bit置1。
upperlim = (upperlim << queenNum) - 1;
queenPos(0, 0, 0);
}
public static void main(String[] args) {
Scanner sc=new Scanner(System.in);
System.out.print("请输入皇后数目:");
int num=sc.nextInt();
long starTime=System.currentTimeMillis();//程序开始时间
QueenTest3 queenTest3 = new QueenTest3();
queenTest3.queen(num);
System.out.println("总共解数为:"+ queenTest3.sum);
long endTime=System.currentTimeMillis();//程序结束时间
double runTimes=(double)(endTime-starTime) / 1000.0;
System.out.println("程序总共运行时间:"+ runTimes + "s");
}
}
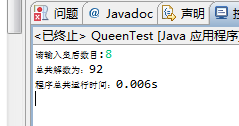
八皇后的效果:(位运算版本)
把上面的代码中的输出结果的去掉:(非位运算版本)
//依次打印本次解皇后的位置
/* for(int m = 1; m <= queenNum; m++){
//System.out.println(x[m]);//这一行用输出当递归到叶节点的时候,一个可行解
//这里只是为了好看才写成下面的
for(int k =1; k <= queenNum;k++){
if(k == x[m]){
System.out.print(x[m]+" ");
}else {
System.out.print("* ");//用*表示没有被用到的位置
}
}
System.out.println();
}
System.out.println();*/然后输出如下:
经过两者对比,发现快了2ms
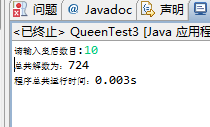
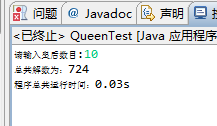
十皇后效果,没想到反而比八皇后的位运算版本还快(十皇后位运算版本)
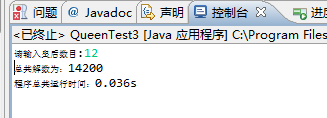
12皇后
位运算
非位运算
(2)C++版本
/*
** 目前最快的N皇后递归解决方法
** N Queens Problem
** 试探-回溯算法,递归实现
*/
#include
using namespace std;
#include
// sum用来记录皇后放置成功的不同布局数;upperlim用来标记所有列都已经放置好了皇后。
long sum = 0, upperlim = 1;
// 试探算法从最右边的列开始。
void test(long row, long ld, long rd)
{
if (row != upperlim)
{
// row,ld,rd进行“或”运算,求得所有可以放置皇后的列,对应位为0,
// 然后再取反后“与”上全1的数,来求得当前所有可以放置皇后的位置,对应列改为1
// 也就是求取当前哪些列可以放置皇后
long pos = upperlim & ~(row | ld | rd);
while (pos) // 0 -- 皇后没有地方可放,回溯
{
// 拷贝pos最右边为1的bit,其余bit置0
// 也就是取得可以放皇后的最右边的列
long p = pos & -pos;
// 将pos最右边为1的bit清零
// 也就是为获取下一次的最右可用列使用做准备,
// 程序将来会回溯到这个位置继续试探
pos -= p;
// row + p,将当前列置1,表示记录这次皇后放置的列。
// (ld + p) << 1,标记当前皇后左边相邻的列不允许下一个皇后放置。
// (ld + p) >> 1,标记当前皇后右边相邻的列不允许下一个皇后放置。
// 此处的移位操作实际上是记录对角线上的限制,只是因为问题都化归
// 到一行网格上来解决,所以表示为列的限制就可以了。显然,随着移位
// 在每次选择列之前进行,原来N×N网格中某个已放置的皇后针对其对角线
// 上产生的限制都被记录下来了
test(row + p, (ld + p) << 1, (rd + p) >> 1);
}
}
else
{
// row的所有位都为1,即找到了一个成功的布局,回溯
sum++;
}
}
int main()
{
int num;
cout<<"请输入皇后数目:";
cin>>num;
clock_t start,finish;
double totaltime;//计算程序运行时间
start=clock();//起始时间
// 因为整型数的限制,最大只能32位,
// 如果想处理N大于32的皇后问题,需要
// 用bitset数据结构进行存储
if ((num < 1) || (num > 32))
{
cout << " 只能计算1-32之间\n";
return 0;
}
// N个皇后只需N位存储,N列中某列有皇后则对应bit置1。
upperlim = (upperlim << num) - 1;
test(0, 0, 0);
cout << "方案共有" << sum;
finish=clock();//结束时间
totaltime=(double)(finish-start)/CLOCKS_PER_SEC;
cout<<"\n此程序的运行时间为"< 输出结果:
下面来对比下java和C++运算的效果:
16皇后C++版本(位运算)
16皇后java版本(位运算)
发现又是java快了点。