2020牛客暑期多校训练营（第九场） Groundhog Chasing Death

原题
题目描述

样例1
输入

1 2 1 2 8 4

输出

2048

样例2
输入

1 2 3 4 120 180

输出

235140177

思路
首先看数据范围，如果直接枚举$x$ⁱ，$y$^j，时间复杂度为$3e6\times 3e6=9e12$，$TLE$等着你。所以我们要想出$O(n)$的算法。
我们先固定$i$，然后把$x$ⁱ和$y$^j$(j：c$~$d)$分解质因数：
$x$ⁱ$=$$q1$^x1$\times$$q2$^x2$\times$$q3$^x3 $\times$$q4$^x4$\dots \dots$
$y$^j$=$$q1$^y1$\times$$q2$^y2$\times$$q3$^y3 $\times$$q4$^y4$\dots \dots$
我们可以把他们最大公因数的函数图像画出来，大概是以下这种情况$：$

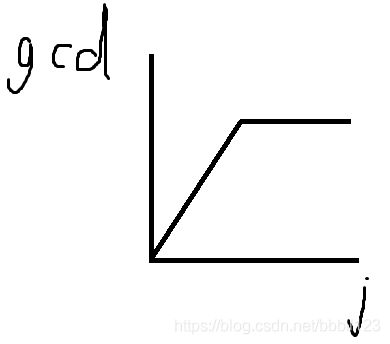
刚开始$gcd$随$j$的增加而增加。后来$x$ⁱ的与$y$每个公共因子$y$^z次方匹配完。所以之后$y$^x到$y$^d与$x$ⁱ的最大公因数不变。观察函数图像，我们会知道$：$

• 前$y$的$z-1$次方与$x$ⁱ的最大公因数递增，可以用等差数列求和。
• 后$y$的$z$次方与$x$ⁱ的最大公因数不变，直接计算即可。

注意$：$最后如果$x>1$，则表示$x$与$y$可能还有质因数，再计算一次即可。
时间复杂度：$O(n)$
代码

#include
#define ll long long
using namespace std;
const ll mod=998244353,md=998244352;
ll a,b,c,d,x,y,z,ans=1,n,u,v;
ll ksm(ll a,ll b)
{
	ll c=1;
	while(b)
	{
		if(b&1)c=c*a%mod;
		a=a*a%mod;b>>=1;
	}
	return c;
}
ll get(ll x,ll y)
{
	ll k=0,p;
	for(int i=1;i<=x;i++)p=u*i/v,p=min(p,y),k=(k+(p+1ll)*p/2%md*v)%md,k=(k+1ll*i*(y-p)%md*u)%md;
	return k;
}
int main()
{
	scanf("%lld%lld%lld%lld%lld%lld",&a,&b,&c,&d,&x,&y);n=max(x,y);
	for(int i=2;i*i<=n;i++,u=0,v=0)
	{
		while(x%i==0)u++,x/=i;while(y%i==0)v++,y/=i;
		if(u&&v)z=(2ll*md+get(b,d)+get(a-1,c-1)-get(a-1,d)-get(b,c-1))%md,ans=1ll*ans*ksm(i,z)%mod;
	}
	if(x^0&&x==y)
	{
		u=v=1;
		z=(2ll*md+get(b,d)+get(a-1,c-1)-get(a-1,d)-get(b,c-1))%md;
		ans=1ll*ans*ksm(x,z)%mod;
	}
	printf("%lld",ans);
	return 0;
}