深入理解带权并查集（例题+思考）

普通的并查集仅仅记录的是集合的关系，这个关系无非是同属一个集合或者是不在一个集合。而带权并查集，不仅记录集合的关系，还记录着集合内元素的关系或者说是元素连接线的权值。这里用三个例题讲解一下吧。

How Many Answers Are Wrong （HDU - 3038）

题目大意：
给你一系列区间和，判断给出的区间中有几个是不合法的。
思考：
1.如何建立区间之间的联系
2.如何发现悖论
首先是如何建立联系，我们可以用一张图表示

假如说区间【fx，x】是之前建立的区间，他们之间和为sum[x]，fx和x的联系可以用集合来存储，同理【fy，y】也是如此。当给出了一个新的区间【x，y】时，且区间和为s。就产生了两种情况了，如果fx == fy 那么这两个区间是有关联的区间，也就是【x，y】之间的和是可以求出的。可以把这个图看成一个向量。 区间【x，y】的和就是可以写成sum[x] - sum[y]。判断给出的s与向量法计算的区间和是否相等就可以判断是否是悖论。
当然如果fx ！= fy就需要建议新的区间关系。首先将fy指向fx，这代表fx是区间的左端点，计算sum【fy】= sum【x】- sum【y】+ s；这里同样用的是向量法。
这样建立联系与判断悖论都可以表达了，接下来就是一些细节了，比如在更新区间的时候要进行路径的压缩，压缩的过程中需要对权值进行更新，目的是使每个已知区间最大化。
代码

#include 

const int maxn = 200000 + 10;

int pre[maxn];
int sum[maxn];    // sum是该节点到其根的和，比如说sum[3],3的根是1，那么sum[3]表示的就是1到3的和……

int find(int x) {
    if (x == pre[x])  return x;
    else {
        int root = find(pre[x]);     // 找到根节点
        sum[x] += sum[pre[x]];       // 权值合并，更新
        return pre[x] = root;        // 压缩路径
    }
}

int main() {
    int n, m;
    while(~scanf("%d%d", &n, &m)) {
        for(int i = 0; i <= n; i++) {
            pre[i] = i;
            sum[i] = 0;
        }
        int x, y;
        int s;
        int ans = 0;
        while(m--) {
            scanf("%d%d%d", &x, &y, &s);
            x--;        // 想一下为什么要减一，可以让类似【1,5】【6,10】这样的区间可以合并……
            int fx = find(x);
            int fy = find(y);
            if (fx != fy) {
                pre[fy] = fx;
                sum[fy] = sum[x] - sum[y] + s;
            }
            else if (sum[y] - sum[x] != s)  ans++;


        }
        printf("%d\n", ans);
    }
    return 0;
}

有了这道题的基础我们可以将带权并查集升级成种类并查集

比如所这道题

A Bug’s Life POJ - 2492

每次给出两个昆虫的关系（异性关系），然后发现这些条件中是否有悖论
就比如说第一组数据

1 2
2 3
1 3
1和2是异性，2和3是异性，然后说1和3是异性就显然不对了。

我们同样可以思考一下这道题如何用带权并查集去做。

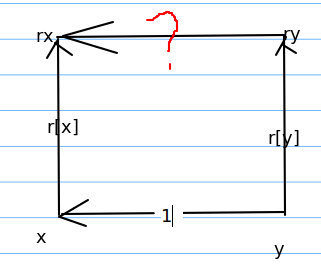
首先用r[x]存储的是x与其根节点rx的关系，0代表同性1代表异性（其实反着也一样因为这个关系是一个环状的）
这道题与上一道题唯一的不同是权值不是累加的关系而是相当于二进制的个位，也就是累加结果取%2。
这样就很容易仿照上一道题写出一下代码

#include 

const int maxn = 2000 + 10;

int pre[maxn];
int r[maxn];  // 与根节点的关系，如果值为1则为异性如果为0则为同性

int find(int x) {
    int t = pre[x];
    if (pre[x] != x) {
        pre[x] = find(pre[x]);
        r[x] = (r[x] + r[t]) % 2;  // 更新关系
    }
    return pre[x];
}

int main() {
   // freopen("input.txt", "r", stdin);
    int flag;
    int kase = 0;
    int T;
    int x, y;
    int n, m;
    scanf("%d", &T);
    while(T--) {
         flag = 1;
         scanf("%d%d", &n, &m);
         for(int i = 1; i <= n; i++) {
             pre[i] = i;
             r[i] = 0;
         }
         while(m--) {
             scanf("%d%d", &x, &y);
             if (!flag) continue;
             int rx = find(x);
             int ry = find(y);
             if (rx == ry) {
                if ((r[x] - r[y]) % 2 == 0) {
                    flag = 0;
                }
             }
             else {
                 pre[rx] = ry;
                 r[rx] = (r[x] - r[y] + 1) % 2;
             }
         }
         printf("Scenario #%d:\n",++kase);
         if(flag)
                printf("No suspicious bugs found!\n\n");
         else
                printf("Suspicious bugs found!\n\n");
    }

    return 0;
}

我们再把上一道题升级一下，从两个种类拓展为三个种类，由于三个种类的关系依旧是一个环所以依然可以套带权并查集模版。有几个种类就取几模，这里是%3

食物链 POJ - 1182

这里给出三种生物的关系，吃与同类的关系。由于这三种生物的关系依旧可以形成一个环，A吃B，B吃C，C又吃A。所以可以套种类并查集模版。
代码

#include

const int maxn = 100000 + 10;

int pre[maxn], r[maxn];    // 父节点，与父节点的关系。0代表同类，1代表吃父节点，2代表被父节点吃。

int Find(int x)
{
    int t = pre[x];
    if(pre[x] != x)
    {
        pre[x] = Find(pre[x]);          // 压缩路径
        r[x] = (r[t] + r[x]) % 3;       // 更新关系
    }
    return pre[x];
}
int main()
{
    freopen("input.txt", "r", stdin);
    int i, N, T, ans;
    scanf("%d%d", &N, &T);
    for(i=0; i<=N; i++) {
        pre[i] = i;
        r[i] = 0;
    }
    ans = 0;
    while(T--)
    {
        int x, y, d;
        scanf("%d%d%d", &d, &x, &y);

        int rx = Find(x);
        int ry = Find(y);
        if(x>N || y>N || (d==2 && x==y) )
            ans++;
        else if(rx == ry && (r[x] - r[y] + 3)%3 != d - 1)
            ans++;
        else if(rx != ry) {
            pre[rx] = ry;
            r[rx] = ((d-1) + r[y] - r[x] + 3) % 3;
        }
    }
    printf("%d\n", ans);
    return 0;
}

ps

这篇文章有什么错误的地方欢迎指正……