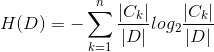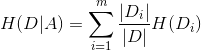机器学习学习笔记（14）----决策树
决策树是一种树结构的机器学习模型。因为其决策过程就像一颗倒置的树，所以叫决策树。举个例子，我们假设去水果摊买水果，我们需要分辨水果的种类，这时可以通过如下的一个简单的决策过程：
通过几个特征规则，我们可以构建一颗决策树，来确定水果的种类。
从上图可以看出，树的叶节点就是最终的决策结果，根节点和非叶子节点用于根据某一特征来决策后面的分支路径。那么问题来了，我们怎么构造这样一棵决策树，哪个特征判据应该放在根节点，哪个特征判据应该放在叶子节点？
为合理量化决策树特征判据的选择标准，可以使用信息论中熵的有关知识对样本的纯度进行定量表示和分析。
信息熵（简称熵，entropy）是信息论中定量描述随机变量不确定度的一类度量指标，主要是用来衡量数据取值的无序程度，熵的值越大，则表明数据取值越杂乱无序。
设
为一个可取有限个值{
}的离散型随机变量，其概率分布为：
,
则随机变量熵定义为：
(1)
如果
，则定义
。显然，如果
的值越大，则随机变量的不确定性就越大。
例如：投掷硬币时，朝上面的是随机变量，其中正面朝上的概率是p，反面朝上的概率为1-p，那么按照(1)式，信息熵是：
(2)
可以通过python绘制这个信息熵函数：
>>> import numpy as np
>>> import matplotlib.pyplot as plt
>>> def entropy(p):
if p in (0,1) :
return 0
h = -p*np.log2(p)-(1-p)*np.log2(1-p)
return h
>>> plot_x = np.linspace(0, 1, 100)
plot_y = np.empty(100)
for i in range(0, 100):
plot_y[i] = entropy(plot_x[i])
>>> plt.plot(plot_x, plot_y)
>>> plt.show()
可以看到
时，信息熵最大，等于1，也就是正反面出现等概率时，随机变量的不确定性最高。
条件信息熵:
设为一个可取有限个值{}的离散型随机变量，
为一个可取有限个值{
}的离散型随机变量，则条件熵定义为：
（3）
可以看出，条件熵是在随机变量条件夏随机变量的熵的数学期望。
经验熵：
具体到一个给定的训练样本集合
，可将集合看成一个关于样本标签取值状态的随机变量，那么按照(1)式，我们可以定义一个量化指标
，用于度量中类型的样本纯度，称为经验熵：
(4)
其中n表示样本标签值的取值状态数，
表示训练样本集中所标注值为第k个取值的训练样本的集合，
和
分别表示集合和的样本数。
经验条件熵：
对于训练样本集上的任意属性
，可以在经验熵的基础上进一步定义一个量化指标
来度量集合中样本以属性为标准划分后的纯度，通常称为集合基于属性的经验条件熵（对应公式(3)）：
(5)
其中m表示属性的取值状态数，
表示集合在以属性为标准划分后所生成的子集，即为中所有属性取第i个状态的样本组成的集合。
信息熵增益：
对于训练样本集上的任意属性，属性关于集合的信息熵增益
定义为经验熵与条件经验熵之差：
（6）
显然，对于属性关于集合的信息熵增益越大，表示使用属性划分后的样本的集合纯度提升越多，决策树模型的分类能力更强，故可以用作为标准选择合适的判别属性。
举个简单例子（数据来自《程序员的AI书：从代码开始》），感受一下决策树的构建：
| 收入 | 公积金 | 是否已婚 | 是否买房子 |
| 中 | 有 | 是 | 是 |
| 低 | 无 | 是 | 否 |
| 低 | 有 | 否 | 否 |
| 高 | 有 | 是 | 是 |
| 中 | 有 | 是 | 否 |
| 高 | 有 | 是 | 是 |
把“是否买房子”作为，经验熵是：
（7）
以“收入”（X1）为属性的条件经验熵是：
(8)
其中收入用X1表示，H1，H2，H3分别表示收入低，中，高的熵。
（9）
(10)
(11)
把H1，H2和H3的结果代入(8)，得
（12）
最终得信息增益
：
（13）
类似的，我们可以算得
（X2表示“公积金”）：
（14）
（X3表示“是否已婚”）：
（15）
这样，我们可以得出收入高低是判断是否买房的主要标准，应该作为决策树的根节点。
参考资料：
《机器学习简明教程》
《程序员的AI书：从代码开始》
《Python机器学习算法：原理，实现与案例》