简介: 最新发布的《Java开发手册(嵩山版)》增加了前后端规约,其中有一条:禁止服务端在超大整数下使用Long类型作为返回。这是为何?在实际开发中可能出现什么问题?本文从IEEE754浮点数标准讲起,详细解析背后的原理,帮助大家彻底理解这个问题,提前避坑。

8月3日,这个在我等码农心中具有一定纪念意义的日子里,《Java开发手册》发布了嵩山版。每次发布我都特别期待,因为总能找到一些程序员不得不重视的“血淋淋的巨坑”。比如这次,嵩山版中新增的模块——前后端规约,其中一条禁止服务端在超大整数下使用Long类型作为返回。
这个问题,我在实际开发中遇到过,所以印象也特别深。如果在业务初期没有评估到这一点,将订单ID这类关键信息,按照Long类型返回给前端,可能会在业务中后期高速发展阶段,突然暴雷,导致严重的业务故障。期望大家能够重视。
这条规约给出了直接明确的避坑指导,但要充分理解背后的原理,知其所以然,还有很多点要思考。首先,我们来看几个问题,如果能说出所有问题的细节,就可直接跳过了,否则下文还是值得一看的:
- 一问:JS的Number类型能安全表达的最大整型数值是多少?为什么(注意要求更严,是安全表达)?
- 二问:在Long取值范围内,2的指数次整数转换为JS的Number类型,不会有精度丢失,但能放心使用么?
- 三问:我们一般都知道十进制数转二进制浮点数有可能会出现精度丢失,但精度丢失具体怎么发生的?
- 四问:如果不幸中招,服务端正在使用Long类型作为大整数的返回,有哪些办法解决?
基础回顾
在解答上面这些问题前,先介绍本文涉及到的重要基础:IEEE754浮点数标准。如果大家对IEEE754的细节烂熟于心的话,可以跳过本段内容,直接看下一段,问题解答部分。
当前业界流行的浮点数标准是IEEE754,该标准规定了4种浮点数类型:单精度、双精度、延伸单精度、延伸双精度。前两种类型是最常用的。我们单介绍一下双精度,掌握双精度,自然就了解了单精度(而且上述问题场景也是涉及双精度)。
双精度分配了8个字节,总共64位,从左至右划分是1位符号、11位指数、52位有效数字。如下图所示,以0.7为例,展示了双精度浮点数的存储方式。
存储位分配
1)符号位:在最高二进制位上分配1位表示浮点数的符号,0表示正数,1表示负数。
2)指数:也叫阶码位。
在符号位右侧分配11位用来存储指数,IEEE754标准规定阶码位存储的是指数对应的移码,而不是指数的原码或补码。根据计算机组成原理中对移码的定义可知,移码是将一个真值在数轴上正向平移一个偏移量之后得到的,即[x]移=x+2^(n-1)(n为x的二进制位数,含符号位)。移码的几何意义是把真值映射到一个正数域,其特点是可以直观地反映两个真值的大小,即移码大的真值也大。基于这个特点,对计算机来说用移码比较两个真值的大小非常简单,只要高位对齐后逐个比较即可,不用考虑负号的问题,这也是阶码会采用移码表示的原因所在。
由于阶码实际存储的是指数的移码,所以指数与阶码之间的换算关系就是指数与它的移码之间的换算关系。假设指数的真值为e,阶码为E ,则有 E = e + (2 ^ (n-1) - 1),其中 2 ^ (n-1) - 1 是IEEE754 标准规定的偏移量。则双精度下,偏移量为1023,11位二进制取值范围为[0,2047],因为全0是机器零、全1是无穷大都被当做特殊值处理,所以E的取值范围为[1,2046],减去偏移量,可得e的取值范围为[-1022,1023] 。
3)有效数字:也叫尾数位。最右侧分配连续的52位用来存储有效数字,IEEE754标准规定尾数以原码表示。
浮点数和十进制之间的转换
在实际实现中,浮点数和十进制之间的转换规则有3种情况:
1 规格化
指数位不是全零,且不是全1时,有效数字最高位前默认增加1,不占用任何比特位。那么,转十进制计算公式为:
(-1)^s*(1+m/2^52)*2^(E-1023)其中s为符号,m为尾数,E为阶码。比如上图中的0.7 :
1)符号位:是0,代表正数。
2)指数位:01111111110,转换为十进制,得阶码E为1022,则真值e=1022-1023=-1。
3)有效数字:
0110011001100110011001100110011001100110011001100110转换为十进制,尾数m为:1801439850948198。
4)计算结果:
(1+1801439850948198/2^52)*(2^-1) =0.6999999999999999555910790149937383830547332763671875经过显示优化算法后(在后文中详述),为0.7。
2 非规格化
指数位是全零时,有效数字最高位前默认为0。那么,转十进制计算公式:
(-1)^s*(0+m/2^52)*2^(-1022)注意,指数位是-1022,而不是-1023,这是为了平滑有效数字最高位前没有1。比如非规格最小正值为:
0x0.0000000000001_2^-1022=2^-52_ 2^-1022 = 4.9*10^-324
3 特殊值
指数全为1,有效数字全为0时,代表无穷大;有效数字不为0时,代表NaN(不是数字)。
问题解答
1 JS的Number类型能安全表达的最大整型数值是多少?为什么?
规约中已经指出:
在Long类型能表示的最大值是2的63次方-1,在取值范围之内,超过2的53次方(9007199254740992)的数值转化为JS的Number时,有些数值会有精度损失。
“2的53次方”这个限制是怎么来的呢?如果看懂上文IEEE754基础回顾,不难得出:在浮点数规格化下,双精度浮点数的有效数字有52位,加上有效数字最高位前默认为1,共53位,所以JS的Number能保障无精度损失表达的最大整数是2的53次方。
而这里的题问是:“能安全表达的最大整型”,安全表达的要求,除了能准确表达,还有正确比较。2^53=9007199254740992,实际上,
9007199254740992+1 == 9007199254740992的比较结果为true。如下图所示:
这个测试结果足以说明2^53不是一个安全整数,因为它不能唯一确定一个自然整数,实际上9007199254740992、9007199254740993,都对应这个值。因此这个问题的答案是:2^53-1。
2 在Long取值范围内,2的指数次整数转换为JS的Number类型,不会有精度丢失,但能放心使用么?
规约中指出:
在Long取值范围内,任何2的指数次整数都是绝对不会存在精度损失的,所以说精度损失是一个概率问题。若浮点数尾数位与指数位空间不限,则可以精确表示任何整数。
后半句,我们就不说了,因为绝对没毛病,空间不限,不仅是任何整数可以精确表示,无理数我们也可以挑战一下。我们重点看前半句,根据本文前面所述基础回顾,双精度浮点数的指数取值范围为[-1022,1023],而指数是以2为底数。另外,双精度浮点数的取值范围,比Long大,所以,理论上Long型变量中2的指数次整数一定可以准确转换为JS的umber类型。但在JS中,实际情况,却是下面这样:
2的55次方的准确计算结果是:36028797018963968,而从上图可看到,JS的计算结果是:36028797018963970。而且直接输入36028797018963968,控制台显示结果是36028797018963970。
这个测试结果,已经对本问题给出答案。为了确保程序准确,本文建议,在整数场景下,对于JS的Number类型使用,严格限制在2^53-1以内,最好还是信规约的,直接使用String类型。
为什么会出现上面的测试现象呢?
实际上,我们在程序中输入一个浮点数a,在输出得到a',会经历以下过程:
1)输入时:按照IEEE754规则,将a存储。这个过程很有可能会发生精度损失。
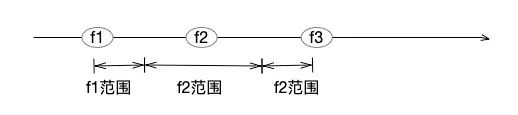
2)输出时:按照IEEE754规则,计算a对应的值。根据计算结果,寻找一个最短的十进制数a',且要保障a'不会和a隔壁浮点数的范围冲突。a隔壁浮点数是什么意思呢?由于存储位数是限定的,浮点数其实是一个离散的集合,两个紧邻的浮点数之间,还存在着无数的自然数字,无法表达。假设有f1、f2、f3三个升序浮点数,且它们之间的距离,不可能在拉近。则在这三个浮点数之间,按照范围来划分自然数。而浮点数输出的过程,就是在自己范围中找一个最适合的自然数,作为输出。如何找到最合适的自然数,这是一个比较复杂的浮点数输出算法,大家感兴趣的,可参考相关论文[1]。
所以,36028797018963968和36028797018963970这两个自然数,对应到计算机浮点数来说,其实是同一个存储结果,双精度浮点数无法区分它们,最终呈现哪一个十进制数,就看浮点数的输出算法了。下图这个例子可以说明这两个数字在浮点数中是相等的。另外,大家可以想想输入0.7,输出是0.7的问题,浮点数是无法精确存储0.7,输出却能够精确,也是因为有浮点数输出算法控制(特别注意,这个输出算法无法保证所有情况下,输入等于输出,它只是尽力确保输出符合正常的认知)。
扩展
JS的Number类型既用来做整数计算、也用来做浮点数计算。其转换为String输出的规则也会影响我们使用,具体规则如下: 
上面是一段典型的又臭又长但逻辑很严谨的描述,我总结了一个不是很严谨,但好理解的说法,大家可以参考一下:
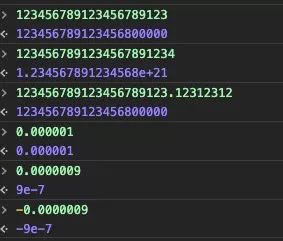
除了小数点前的数字位数(不算开始的0)少于22位,且绝对值大于等于1e-6的情况,其余都用科学计数法格式化输出。举例:
3 我们一般都知道十进制数转二进制浮点数有可能会出现精度丢失,精度丢失怎么发生的?
通过前面IEEE754分析,我们知道十进制数存储到计算机,需要转换为二进制。有两种情况,会导致转换后精度损失:
1)转换结果是无限循环数或无理数
比如0.1转换成二进制为:
0.0001 10011001100110011001100110011...其中0011在循环。将0.1转换为双精度浮点数二进制存储为:
0 01111111011 1001100110011001100110011001100110011001100110011001按照本文前面所述基础回顾中的计算公式 (-1)^s_(1+m/2^52)_2^(E-1023)计算,可得转换回十进制为:0.09999999999999999。这里可以看出,浮点数有时是无法精确表达一个自然数,这个和十进制中1/3 =0.333333333333333...是一个道理。
2)转换结果长度,超过有效数字位数,超过部分会被舍弃
IEEE754默认是舍入到最近的值,如果“舍”和“入”一样接近,那么取结果为偶数的选择。
另外,在浮点数计算过程中,也可能引起精度丢失。比如,浮点数加减运算执行步骤分为:
零值检测 -> 对阶操作 -> 尾数求和 -> 结果规格化 -> 结果舍入其中对阶和规格化都有可能造成精度损失:
- 对阶:是通过尾数右移(左移会导致高位被移出,误差更大,所以只能是右移),将小指数改成大指数,达到指数阶码对齐的效果,而右移出的位,会作为保护位暂存,在结果舍入中处理,这一步有可能导致精度丢失。
- 规格化:是为了保障计算结果的尾数最高位是1,视情况有可能会出现右规,即将尾数右移,从而导致精度丢失。
4 如果不幸中招,服务端正在使用Long类型作为大整数的返回,有哪些办法解决?
需要分情况。
1)通过Web的ajax异步接口,以Json串的形式返回给前端
方案一:如果,返回Long型所在的POJO对象在其他地方无使用,那么可以将后端的Long型直接修改成String型。
方案二:如果,返回给前端的Json串是将一个POJO对象Json序列化而来,并且这个POJO对象还在其他地方使用,而无法直接将其中的Long型属性直接改为String,那么可以采用以下方式:
String orderDetailString = JSON.toJSONString(orderVO, SerializerFeature.BrowserCompatible);SerializerFeature.BrowserCompatible 可以自动将数值变成字符串返回,解决精度问题。
方案三:如果,上述两种方式都不适合,那么这种方式就需要后端返回一个新的String类型,前端使用新的,并后续上线后下掉老的Long型(推荐使用该方式,因为可以明确使用String型,防止后续误用Long型)。
2)使用node的方式,直接通过调用后端接口的方式获取
方案一:使用npm的js-2-java的 java.Long(orderId) 方法兼容一下。
方案二:后端接口返回一个新的String类型的订单ID,前端使用新的属性字段(推荐使用,防止后续踩坑)。
引用
[1] http://citeseerx.ist.psu.edu/viewdoc/summary?doi=10.1.1.52.2247&rank=2
[2]《码出高效》