基于音乐识别的频谱转换算法——常数Q变换CQT（转载修改）

傅立叶变换的缺点

由于在音乐中，所有的音都是由若干八度的12平均律共同组成的，这十二平均律对应着钢琴中一个八度上的十二个半音。这些半音临近之间频率比为2^1/12。显然，同一音级的两个八度音，高八度音是低八度音频率的两倍。

因此在音乐当中，声音都是以指数分布的，但我们的傅立叶变换得到的音频谱都是线性分布的，两者的频率点是不能一一对应的，这会指使某些音阶频率的估计值产生误差。所以现代对音乐声音的分析，一般都采用一种具有相同指数分布规律的时频变换算法——CQT。

什么是恒Q变换（CQT）

CQT指中心频率按指数规律分布，滤波带宽不同、但中心频率与带宽比为常量Q的滤波器组。它与傅立叶变换不同的是，它频谱的横轴频率不是线性的，而是基于log2为底的，并且可以根据谱线频率的不同该改变滤波窗长度，以获得更好的性能。由于CQT与音阶频率的分布相同，所以通过计算音乐信号的CQT谱，可以直接得到音乐信号在各音符频率处的振幅值，对于音乐的信号处理来说简直完美。

关于信号处理中的窗口

在实际的信号处理过程中，我们会将时间片段分帧，按照帧为单位，转换成一个基于时间帧的频谱图，然后我们再将这些频谱图放到时间轴上，就可以形成一个类似热力图样的，基于时间变换的频谱变换图。

现在我们注意一个问题，在我们的单个时间帧内（实际上我们在对信号进行截断），信号很可能不呈现它原周期的整数倍（周期截断），那么截断后的信号会泄漏问题，为了更好地满足傅立叶变换（实际上是FFT）处理的周期性要求，我们需要使用加权函数，也叫窗函数。加窗主要是为了使时域信号似乎更好地满足FFT处理的周期性要求，减少泄漏。

我们关注上述“中心频率与带宽比为常量Q”，从公式上看，我们可以表达为下述公式

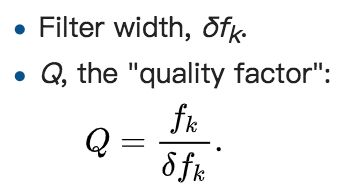
直观的理解是，恒Q变换避免了时频分辨率均匀的缺点，对于低频的波，它的带宽十分小，但有更高的频率分辨率来分解相近的音符；但是对于高频的波，它的带宽比较大，在高频有更高的时间分辨率来跟踪快速变化的泛音。

假设处理的最低音为f_min，f_k表示第k分量的频率，b为一个八度内所包含的频谱线数，例如b=36，表示每个八度内有36条频谱线，每个半音三条频率分量。
$$K=\lceil b\cdot lo{g}_2(\frac{f_{max}}{f_{min}})\rceil$$

（向上取整）
$$f_k=2^{k/b}{f}_{min}，k=0,1...,K-1$$

并且有
$$f_{k+1}-f_k=f_k(2^{1/b}-1)$$

即
$$f_k=f_{min}\cdot 2^{k/b}，k=0,1,...,K-1$$

设 δ_f 表示的是频率 f 处的频率带宽，也可以称为频率解析度，那么根据定义得知：
$$Q=\frac{f}{{\delta }_f}=\frac{1}{2^{1/b}-1}$$

得知常量Q是只与b相关的常数。

假设N_k是随频率变换的窗口长度，fs表示采样频率：
$$N_k=\lceil Q\frac{f_s}{f_k}\rceil ，k=0,1...,K-1$$

同时我们的线性频率应该变为基于log2的非线性频率

CQT通过采用不同的窗口宽度，获得不同的频率解析度，从而可以得到各个半音的频率振幅。在CQT中第n帧的第k个半音频率分量可表示为
$$X^{CQT}(k)=\frac{1}{N_k}\sum _{n=0}^{N_k-1}x(n)w_{N_k}(n)e^{-j\frac{2\pi Q}{N_k}n}$$

其中， w(n)是长度为N_k的窗函数；Q是CQT变换中的常数因子；k是CQT谱的频率序号；N_k值与k值有关。

Reference
[1]陈燕文, 李坤, 韩焱, et al. 基于多特征融合的乐器声品质评价方法研究[J]. 测试技术学报, 2019(5).
[2]https://www.jianshu.com/p/53c93947c417