【java算法】贪心算法-(贪心算法的基本要素、最小生成树、哈夫曼编码)
文章目录
- 贪心算法
- 贪心算法与动态规划的区别
- 贪心选择性质
- 哈夫曼编码
- 最小生成树
- 克鲁斯卡尔算法
- Prim
贪心算法
假设有4种硬币,它们的面值分别为二角五分、一角、五分和一分。现在要找给某顾客六角三分钱。这时,很自然会拿出2个二角五分的硬币,1个一角的硬币和3个一分的硬币交给顾客。这种找硬币的方法与其他找法相比,所拿硬币个数是最少的。其实这里用到的找硬币算法就是:首先选出一个面值不超过六角三分的最大硬币,即二角五分,然后从剩下的硬币中选出面值不超过三角八分的最大硬币,一直如此下去直到找到。这个找硬币的方法实际上就是贪心算法。
贪心算法总是做出在当前看来最好的选择,也就是说贪心算法并不从整体最优考虑,它所做出的选择只是在某种意义上的局部最优的选择。当然,希望贪心算法得到的最终结果也是整体最优的。上面所说的找硬币算法得到的结果是整体最优解。找硬币问题本身具有最优子结构性质,它可以用动态规划算法求解。但用贪心算法更简单、更直接,且解题效率更高。
贪心算法利用了问题本身的一些特性。例如,上述找硬币的算法利用了硬币面值的特殊性。如果硬币的面值改为一分、五分和一角一分,而要找给顾客的是一角五分钱。还用贪心算法,找给顾客一个一角一分和4个一分的硬币。然而3个五分的硬币显然是最好的找法。虽然贪心算法不能对所有问题都得到整体最优解,但是对许多问题它能产生整体最优解。例如,图的单源最短路径问题,最小生成树等。在一些情况下,即使贪心算法不能得到整体最优解,其最终结果却是最优解的很好近似。
贪心算法与动态规划的区别
**所谓贪心选择性质是指所求问题的整体最优解可以通过一系列局部最优的选择,即贪心选择来达到。**这是贪心算法可行的第一个基本要素,也是贪心算法与动态规划算法的主要区别。
- 在动态规划算法中,每步所做出的选择往往依赖于相关子问题的解。因而只有在解出相关东西后,才能做出选择。
- 在贪心算法中,仅在当前状态下做出最好选择,即局部最优选择。然后再去解释做出这个选择后产生的相应的子问题。贪心算法所做出的的贪心选择可以依赖于以往所做过的选择,但绝不依赖于将来所做的选择,也不依赖于子问题的解。
正是由于这种差别,动态规划算法通常以自底向上的方式解各子问题,而贪心算法则通常以自顶向上的方式进行,以迭代的方式做出相继的贪心选择,每做出一次贪心选择就将所求问题简化为规模更小的子问题。
例:比如0-1背包可以用动态规划求解
背包问题用贪心算法求解
贪心选择性质
对于一个具体问题,要确定它是否具有贪心选择性质,必须证明每一步所做出的贪心选择最终导致问题的整体最优解。通常可以用类似于证明活动安排问题的贪心选择性质时所采用的方法来证明。首先考查问题的一个整体最优解,并证明可修改这个最优解,使其以贪心选择开始。做出贪心选择后,原问题简化为规模更小的类似子问题。然后,用数学归纳法证明,通过每一步做贪心选择,最终可得到问题的整体最优解。其中,证明贪心选择后的问题简化为规模最小的类似子问题的关键在于利用该问题的最优子结构性质。
当一个问题的最优解包含其子问题的最优解时,称此问题具有最优子结构性质。问题的最优子结构性质是该问题可用动态规划或贪心算法求解的关键特征。
哈夫曼编码
其实当我们看到问题时,先想清楚他的结构,才能更好的设计类,
什么是哈夫曼树?
假设有n个权值{w1,w2,……,wn},试构造一颗有n个叶子结点的二叉树,每个叶子结点带权为w1,则其中带权路径长度WPL最小的二叉树称为最优二叉树或哈夫曼树。

我们可以看到,将权值大的和路径短的放在一起,此时乘积最小。
那么如何构造呢?

书上给出这样的算法,我们给出具体的场景来分析
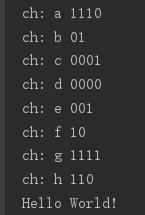
已知某系统在通信联络中只可能出现8种字符,其概率分别为0.05,0.29,0.07,0.08,0.14,0.23,0.11,试设计哈夫曼编码。
设权w=(5,29,7,8,14,23,3,11),n=8,则m=15,按上述算法可构造一颗哈夫曼树
我们按照上述方法,将每个权值看成一个哈夫曼节点,按照算法的意思,取最小的两个,生成一个树根节点为权值之和,在原数组中将这两个节点删除,将新的树插入到原数组,这时再取最小值取得就是这个树的整体。

我们设左子树为1,右子树为0
则每个编码如右图,和之前数字图像处理中的哈夫曼编码的方法求解出来的结果一样
那我们具体怎么实现呢?
- 做准备工作:将结构设计出来,包括哈夫曼节点,哈夫曼树
- 我们需要一个找第一小和第二小的算法
简单理解,每次找最小就用到了贪心选择
设计的类
```java
class HuffNode
{
public int weight=0;
public int parent=0;
public int leftchild=0;
public int rightchild=0;
public HuffNode()
{}
}
class HuffCode
{
char ch;
char []code;
public HuffCode(char x,int n)
{
ch = x;
code =new char[n];
code[n-1]='\0';
}
}
这是设计一个保存树结构的Node类和保存编码的Code类
```java
class HuffManTree
{
final static int LEAFSIZE = 8;
final static int SUMSIZE = (LEAFSIZE*2);
HuffNode []hft = null;
HuffCode []hcd = null;
public HuffManTree()
{
hft = new HuffNode[SUMSIZE];
for(int i = 0;i hft[j].weight)
{
i = j;
}
}
hft[i].parent = -1;
return i;
}
public void CreateHuffTree()
{
int i = LEAFSIZE+1;
while(i 核心代码是构建,CreateHuffTree,其实就是找到最小的两个节点更新左右孩子父节点,已经被选过的节点的父节点置为-1,防止重复选择
最小生成树
设G=(V,E)是无向连通带权图,即一个网络。E中每条边(v,w)的权为c[v][w]。如果G的子图G是一颗包含G的所有顶点的树,则称G’为G的生成树。生成树上各边权的总和称为该生成树的耗费。在G的所有生成树中,耗费最小的生成树称为G的最小生成树。
实际意义:最小生成树给出了建立通信网络的最经济的方案
解决这个问题我们先来解决图的问题。
图可以分为
有向图与无向图
完全图
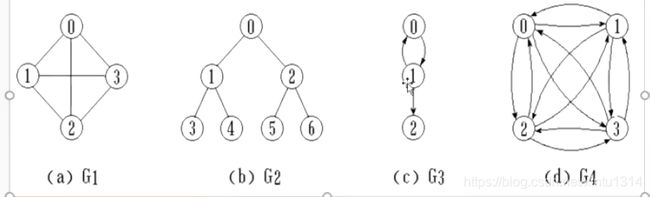
简单路径:路径上的各点均不互相重复
我们举一个例子来理解图

上图是一个图,双向图,1——》2,2——》1,但是1不能到3
我们可以用右边的二维数组来表示之间的关系,可以到的就是1,不能到的就是0
我们可以根据思路来设计代码
这是来初始化一个图的代码
将可以走的路径设为1
class Graph
{
int vernum;//节点个数
int arcnum;//路径个数
char []verlist;
int [][]edges;
public Graph()
{
vernum = 0;
arcnum = 0;
verlist = null;
edges = null;
}
void InitGraph()
{
vernum = 6;
arcnum = 10;
verlist = new char[vernum+1];
for(int i = 0;i<vernum;++i)
{
verlist[i] = (char)( 'A'+i);
}
edges = new int[vernum][vernum]; // 6 * 6
for(int i = 0;i<vernum;++i) edges[i][i]= 0;
int []begin={0,0,0,1,1,2,2,2,3,4};
int []end ={1,2,3,2,4,3,4,5,5,5};
for(int i = 0;i<arcnum;++i)
{
int v = begin[i];
int u = end[i];
edges[v][u] = 1;
edges[u][v] = 1;
}
}
void Print()
{
System.out.println("verlist");
for(int i = 0;i<vernum;++i)
{
System.out.printf("%c ",verlist[i]);
}
System.out.println();
System.out.println("Edges");
for(int i = 0;i<vernum;++i)
{
for(int j = 0;j<vernum;++j)
{
System.out.printf("%4d",edges[i][j]);
}
System.out.println();
}
System.out.println();
}
void DFS(int v,boolean []visited)
{
visited[v] = true;
System.out.println(verlist[v]);
for(int j = vernum-1;j>=0;--j)
{
if(!visited[j] && edges[v][j] == 1)
{
DFS(j,visited);
}
}
}
void BFS()
{
int v = 0;
boolean []visited = new boolean[vernum];
for(int i = 0;i<vernum;++i) visited[i] = false;
Queue<Integer> qu = new LinkedList<Integer>();
qu.offer(v);
visited[v] = true;
while(!qu.isEmpty())
{
v = qu.poll();
System.out.println(verlist[v]);
for(int j = 0;j<vernum;++j)
{
if(!visited[j] && edges[v][j] == 1)
{
qu.offer(j);
visited[j] = true;
}
}
}
System.out.println();
}
}
public class GraphTest {
public static void main(String[] args)
{
Graph gh = new Graph();
gh.InitGraph();
gh.Print();
gh.BFS();
System.out.println("Hello World!");
}
并查集
等价关系和等价类
等价类:从数学上看,等价类是一个对象(或成员)的集合,在此集合中所有对象应满足等价关系

构建并查集

节点:0 1 2 3 4 5 6 7 8 9 10 11
双亲:-5 3 0 -3 0 3 -4 0 6 8 6 2
class UFSets {
int[] parent;
int size;
public UFSets(int sz) {
parent = new int[sz];
size = sz;
for (int i = 0; i < size; ++i) {
parent[i] = -1;
}
}
public int FindRoot(int child)
{
while(parent[child] >= 0)
{
child = parent[child];
}
return child;
}
public boolean Union(int ac,int bc)
{
boolean tag = false;
int pac = FindRoot(ac);
int pbc = FindRoot(bc);
if(pac != pbc)
{
parent[pac] += parent[pbc];
parent[pbc] = pac;
tag = true;
}
return tag;
}
void Print(int pa)
{
System.out.printf(" %d ",pa);
for(int i = 0;i<size;++i)
{
if(parent[i] == pa)
{
Print(i);
}
}
}
public void PrintSet()
{
int k = 1;
for(int i = 0;i<size;++i)
{
if(parent[i] < 0)
{
System.out.printf("第 %d 集合 \n",k++);
Print(i);
System.out.println();
}
}
}
现在我们开始构建树——
克鲁斯卡尔算法
class MinSpanNode
{
int head=-1;
int tail=-1;
int cost=0; //
public MinSpanNode()
{
}
public MinSpanNode(int ha, int ta,int ct)
{
head = ha;
tail = ta;
cost = ct;
}
}
class MinSpanTree
{
MinSpanNode []data;
int size;
public MinSpanTree()
{
data = null;
size = 0;
}
public void CreateMinSpan(Graph1 gh)
{
int n = gh.GetVer();
UFSets st = new UFSets(n);
Comparator<MinSpanNode> DisCost = new Comparator<MinSpanNode>() {
@Override
public int compare(MinSpanNode first, MinSpanNode second) {
if(first.cost > second.cost)
{
return 1;
}else if(first.cost < second.cost)
{
return -1;
}else
{
return 0;
}
}
};
Queue<MinSpanNode> pri = new PriorityQueue<MinSpanNode>(gh.vernum,DisCost);
for(int i = 1;i<gh.vernum;++i)
{
for(int j = 0 ; j<i;++j)
{
if(gh.edges[i][j] != 0x7fffffff)
{
MinSpanNode x = new MinSpanNode(i,j,gh.edges[i][j]);
pri.add(x);
}
}
}
size = n - 1; //
data = new MinSpanNode[size];
int i = 0;
while(i<size && !pri.isEmpty())
{
MinSpanNode x = pri.poll();
if(st.Union(x.head,x.tail)) {
data[i] = x;
++i;
}
}
}
public void Print()
{
for(int i = 0;i<size;++i)
{
System.out.printf(" %d head -> %d tail=> %d cost \n",data[i].head,data[i].tail,data[i].cost);
}
}
}
按权的递增顺序查看的边的序列可以看作一个优先队列,它的优先级为边权。顺序查看等价于对优先队列执行removeMin运算。可以用优先级队列。
Prim
public void Prim(Graph1 gh)
{
int v = 0;
int n = gh.GetVer();
size = n - 1;
data = new MinSpanNode[size];
int k = 0;
for(int i = 0;i<n && k < size ;++i)
{
if(i != v)
{
MinSpanNode x = new MinSpanNode(v,i,gh.edges[v][i]);
data[k] = x;
++k;
}
}
//////////////////////////////////
for(int i = 0;i<size-1;++i)
{
int minid = i;
for(int j = i+1;j<size;++j)
{
if(data[minid].cost > data[j].cost)
{
minid = j;
}
}
///////////////////
if(i != minid)
{
MinSpanNode x = data[i];
data[i] = data[minid];
data[minid] = x;
}
int u = data[i].tail;
for(int j = i+1;j<size;++j)
{
if(data[j].cost > gh.edges[u][data[j].tail] )
{
data[j].head = u;
data[j].cost = gh.edges[u][data[j].tail];
}
}
}
}