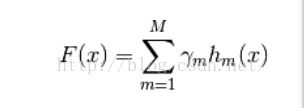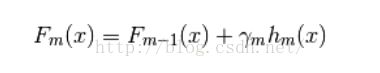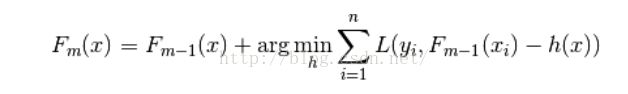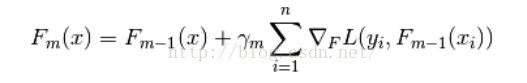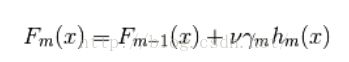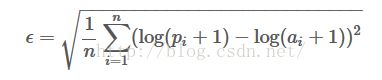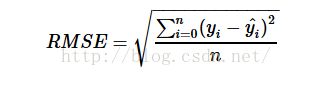机器学习模型（一） GBDT

 

一、   概述

GBDT（GradientBoosting Decision Tree）/ GBRT（Gradient Boosting Regression Trees），是一个比较广泛的概念，可以使用不同的损失函数解决分类回归问题，但值得注意的是这里用的决策树总是“回归树”。同时，也是一个准确的，有效的，现成的可以用于回归或者分类问题的模型。包括网页搜索和生态学都有应用。

二、   原理

i.             模型（假设函数）

其中：

    是弱学习其的假设函数

即：

对每个弱分类器结果进行累加

ii.             算法

      

     逐步迭代，其中是能够使得当前模型损失函数最小的

      即:

   

   

      GradientBoosting求解这个最小化问题的方法是：总是往损失函数的负梯度方向移动，即

  

  

注：计算损失函数的负梯度在当前模型的值，将它作为残差的估计，对于平方损失函数它就是残差，对于一般损失函数，它就是残差（预测值与真实值的差）的近似值，对于分类问题，实际处理可以加入logistic变化。

 

对于步长，使用线搜索（Line Search）的方法，即：

  

iii.             策略（损失函数）

1.   回归

a.  最小二乘/均方差/Least squares

b.  最小绝对偏差/Least absolutedeviation

c.  Huber损失函数（a和b的结合，对异常值不敏感）

d.  分位数（分位数回归使用的损失函数，可以得到预测区间）

2.   分类

e.  二项式损失（二分类问题）

f.  多项式损失（对于类别数量较多的分类效率较低）

g.  指数损失（与AdaBoost相同的损失函数，对于缺失标记的数据处理没有前两者好，只能用于二分类问题）

iv.             正则化

1.   缩减（Shrinkage）

a.  Idea

更小的学习率，逐步接近，效果比大的学习率要好

b.  原理

   增加参数作为学习率，一般设置为< 0.1

2.   子采样（Subsampling）

a.  与bagging(Bootstrap averaging)结合

即自助法采样，每一步迭代都进行重新采样（有放回的）

b.  对特征进行子采样

即类似随机森林，对特征进行随机采样

c. 备注

对于out-of-bag数据，可以使用OOB估计，但通常情况下使用交叉验证会比较好

v.             解释性

1.   特征重要性评价

即认为：特征A越多被用作单棵树的分支节点，那么它就越重要

所以我们可以对某特征在所有单棵树上的重要性（作为分支节点的数量）作平均值

2.    局部依赖图

关注目标特征（通常只选择一到三个特征）与目标函数之间的关系（由局部函数依赖计算），直接汇出图，判断，是否相关，何时相关，如何相关

其中，局部依赖的计算方法为：

1、 计算单棵树所有被遍历到的叶子的权值平均

a.  从根节点开始遍历，如果分支节点与目标特征有关，则转向对应的左分支或右分支；如果无关，则左右分支都继续遍历

b.  最终，函数结果是所有被遍历到的叶子的权值平均。其中权值是训练集中进入某分支的数量

2、 将每棵树的结果再次进行平均

3、 实验证明这样的函数对于决策树可以高效的得到局部依赖关系而不依赖于具体的训练数据

vi.             优劣

1.   优

a.  可以处理多种类型的数据（连续型，离散型）

b.  高准确率

c.  通过误差函数（如Huber Loss），使得程序鲁棒性较好（对outlier不敏感）

d.  不易过拟合（总是更加关注错误的类别，逐步求解，通过对单棵树深度的限制，使用了较少的特征）

2.   劣

e.  需要作归一化

f.  属于boosting方法，并行化较难

三、   应用

1.   预测Yelp评论中得到"Useful"的票数

a.      模型判断

回归模型，GBDT(Regressor)

b.      数据

Yelp 提供的250M（约120万条数据）

c.       特征（共36个）

                                      i.  评论日期(对于某绝对时间的相对日期)(date)

                                     ii.  评论目标商家的等级数(stars)

                                   iii.   评论长度(review_len)

                                     iv.  词干化后的评论长度(stem_len)

                                      v.  词干化后去除重复单词的评论长度(stem_unipue_len)

                                     vi.  300个聚类中心下的类别(clust_300)

                                   vii.   500个聚类中心下的类别(clust_500)

                                 viii.   750个聚类中心下的类别(clust_750)

                                     ix.  1000个聚类中心下的类别(clust_1000)

                                      x.  评论对应商户周i的checkin总数(checkin_di)

                                     xi.  对应商户获得的评论数（与其check_all总数相除得到一个比值）（w_count_store）

                                   xii.   对应客户发出的评论总数（与其check_all总数相除得到一个比值）（w_count）

                                 xiii.   评论的平均用户评分是与当前评论获得的评分之差（delta_user_review_star）

                                   xiv.   对应商户获得的平均评分与当前评论获得的评分之差（delta_review_business_star）

                                     xv.  获得”cool/funny/useful”的得票数（与review总数作差）

d.      参数设置

                                         i.     迭代次数：400

                                       ii.     树的深度：4

e.      评价标准（回归）

 i.     线上

平方根对数误差（RMSLE）

  其中：

  N是评论总数

  P是预测为useful的数量（对于评论i）

  A是实际的useful数量（对于评论i）

 ii.     线下

1.  RMSLE

2.  RMSE

即：使用欧式距离

  但平均值对异常点敏感，非鲁棒性，所以可以用分位数来替代平均数

3.  MAPE

即：使用相对误差的中位数

f.        对回归结果进行解释

 i.     特征重要性

将Yelp提供的数据放入模型，输出特征重要性：

[0.13744402  0.01273528  0.03524743 0.01961557  0.02436443  0.02966849

  0.03414323 0.02825288  0.02709121  0.0299446  0.02945635  0.02395466

  0.02081807 0.0264301   0.02784376  0.01271173 0.01977887  0.01872961

  0.0212326  0.0207145   0.02266258  0.01709742 0.0201273   0.0153837

  0.01610106 0.01900703  0.00754138  0.01574936 0.01609759  0.04067123

  0.02745899 0.03278133  0.00955519  0.05214835 0.03273104  0.05470907]

可以看出，第一个特征（Date）的占用的权值最多，也就是在许多棵树里出现了。一方面，说明Date总是被分错，使得模型严重关注他，另一方面，可能Date可能是一个相关性不大的特征

 ii.     局部依赖图

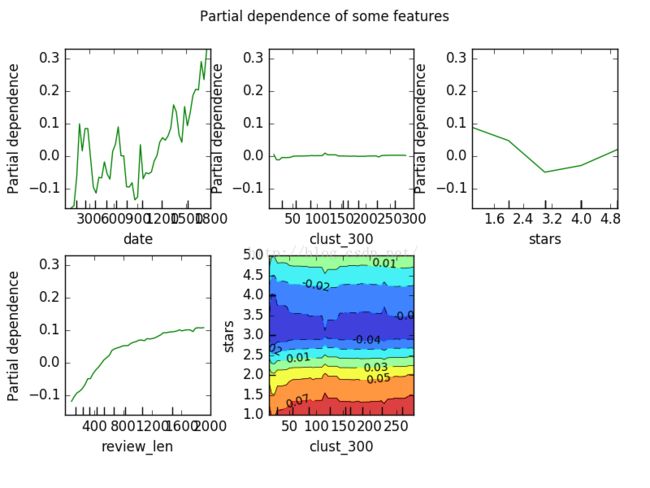
这里我们选用几个典型的特征绘图观察（当然包括Date）

图1：

可以看到，对于Date，日期的变化，纵轴的几乎是无规律，这也就意味着，Date与评论是否获得点赞几乎是没有关系，也恰与“特征重要性”一栏相对应

同时，也注意到，评论长度的变化，纵轴大致缓缓向上（类似倒抛物线），说明评论长度与评论获赞存在较强的相关性（可能是多项式相关）

对于彩色图，则结合了两个特征，聚类中心为300和商家获得的星标数，可以看到，当固定纵轴时，对于横轴的变化，相关性变化微乎其微，说明聚类中心为300几乎对最后票数预测没什么帮助。而固定横轴时，可以看到相关指数变化在变小，说明商铺的星标数与最后的获赞票数有关