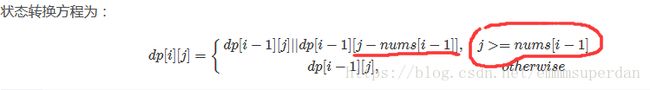emmmsuperdan
emmmsuperdan

动态规划之划分两个和相同的子集

题目描述：

给一 只含有正整数的非空数组, 找到这个数组是否可以划分为 两个 元素和相等的子集。

注意事项：
所有数组元素不超过100.
数组大小不超过200.

样例：
给一数组 [1, 5, 11, 5] , 返回 true ,
两个子集:[1, 5, 5], [11]
给一数组 [1, 2, 3, 9] , 返回 false

 

思路：首先判断元素总和，如果是奇数一定分不出；
 

是偶数的话，就用动态规划：dp[i][j]表示在第一个到第i个元素集中，是否存在和为j的布尔值；

sum=sum/2;

int[][] dp=new int[len+1][sum+1];

 

套路基本就是dp【i】【j】，i表示数目之类的，而j就用来表示总和，总价值之类的；

dp【i】【j】=dp【i-1】【j】（表示从dp[i-1][j]到dp[i][j]就没拿东西（总数没变））

dp【i】【j】=dp【i-1】【j-A【i-1】】(表示dp【i-1】【j-A【i-1】】到dp[i][j]拿了东西（因为总数加上了A[i-1]）)

 

横坐标表示j从1---》sum之间，若j大于nums[i-1]的话，那就用j，那么总数就变成了[j-[nums[i-1]]],（即j表示零钱数，为什么j能替换掉nums[i-1]，因为j比它大；如果j比nums[i-1]小的话,[j-[nums[i-1]]]是不存在的，也就不能代替nums[i-1]了）

动态规划之划分两个和相同的子集_第1张图片

 

你可能感兴趣的:(java算法)

  • Java算法之LRUCache缓存实现 持续输出... #Java算法java算法缓存
    实现一个LRU（最近最少使用）缓存可以通过使用HashMap和双向链表来实现。HashMap用于快速查找缓存中的元素，而双向链表用于维护元素的使用顺序实现思路：1.使用HashMap存储键值对，以便快速访问。2.使用双向链表维护元素的使用顺序，最近使用的元素放在链表头部，最少使用的元素放在链表尾部。3.每次访问或插入元素时，将该元素移动到链表头部。4.当缓存容量达到上限时，移除链表尾部的元素。5.
  • Java算法之判断平衡二叉树 持续输出... #Java算法算法
    判断一棵二叉树是否是平衡二叉树（即AVL树）是一个常见的问题。平衡二叉树的定义是：对于树中的每个节点，其左右子树的高度差不超过1。我们可以通过递归的方法来判断一棵二叉树是否是平衡的packagecom.huawei.od.huawei.algorithm;/***@ClassName:IsBalancedBinaryTree是否是平衡二叉树*@Desc:判断一棵二叉树是否是平衡二叉树（即AVL树）
  • Java算法之归并排序（Merge Sort） 持续输出... #Java算法算法java排序算法
    归并排序简介归并排序是一种采用分治法的排序算法，它将排序问题分解为多个较小的子问题来解决，然后将这些子问题的解合并以得到原问题的解。归并排序以其稳定性和高效率而著称，尤其适用于大数据集的排序。算法原理归并排序的基本步骤包括：分解：将数组递归地分成两半，直到每个子数组只有一个元素。解决：由于每个只有一个元素的子数组自然是有序的，不需要排序。合并：将已排序的子数组合并成更大的有序数组，直到最终得到完全
  • Java算法之冒泡排序（Bubble Sort） 持续输出... #Java算法算法java
    冒泡排序简介冒泡排序是一种基础的排序算法，以其简单性和直观性而著称。它通过重复遍历待排序的数列，比较每对相邻元素，并在必要时交换它们的位置，从而实现排序。算法原理冒泡排序的基本思想是：通过重复遍历整个数组，每次遍历都会将最大的元素“冒泡”到它应该在的位置。这个过程会一直重复，直到整个数组变得有序。代码实现以下是使用Java实现冒泡排序的示例代码：publicclassBubbleSort{publ
  • Java算法之TimSort 持续输出... #Java算法算法java排序算法
    TimSort简介TimSort是一种高效的排序算法，由TimPeters于2002年设计，主要特点是结合了归并排序（MergeSort）和插入排序（InsertionSort）的优点。这种算法在很多编程语言的默认排序函数中得到应用，如Python的sort()和Java的Arrays.sort()。算法原理TimSort的工作原理如下：分解：将待排序数组分解为小的有序序列，每个序列长度为minr
  • Java算法之梳排序（Comb Sort） 持续输出... #Java算法算法
    梳排序简介梳排序（CombSort）是冒泡排序的一个变种，其核心思想是在比较相邻元素之前先进行更大步长的比较。这种算法的名称来源于其工作方式类似于梳头发时的动作，先大范围地移动，然后逐渐减小移动的步长，直至相邻。算法原理梳排序的工作原理包括以下几个步骤：初始化步长：设置一个初始步长，通常为数组长度的缩放因子，如gap=n/1.3。比较与交换：从数组的开头开始，比较相隔gap个元素的两个数，如果前一
  • Java算法之希尔排序（Shell Sort） 持续输出... #Java算法算法java排序算法
    简介希尔排序，又称为缩小增量排序，是插入排序的一种改进算法。它通过引入增量序列，将原始数据序列分成多个子序列，对每个子序列进行插入排序，然后逐渐减小增量，直到增量为1，完成整个排序过程。算法步骤选择一个增量序列，例如初始时为数组长度的一半。将数组分为多个子序列，每个子序列的元素间隔为增量序列的第一个值。对每个子序列进行直接插入排序。逐步减小增量序列的值，重复步骤2和3，直到增量为1。//shell
  • Java算法之插入排序（Insertion Sort） 持续输出... #Java算法算法java排序算法
    插入排序简介插入排序是一种简单直观的排序算法，它的工作原理是通过构建有序序列，对于未排序数据，在已排序序列中从后向前扫描，找到相应位置并插入。这个过程像打牌时整理手中的牌一样，逐步将数据排列成有序。算法原理插入排序的工作原理如下：将第一元素视为已排序的序列。从未排序序列中取第一个元素，从已排序序列的末尾开始比较。比较如果已排序序列中的元素比待插入元素大，则将已排序序列的元素向后移动一位。重复步骤3
  • Java算法 —— 二分查找（图解、代码展示） 肥兄 Java基础算法二分查找算法java经验分享
    概述：普通查找和二分查找的区别：普通查找：首先要遍历数组，获取每个元素，判断当前遍历的元素是否和要查找的元素相同，相同的话就返回该元素的索引，没找到，手动返回-1二分查找：每一次都要去获取数组的中间索引对应的元素，然后和要查找的元素进行比对。如果相同，返回索引值。如果不同，就比较中间元素和要查找的元素值。1、如果中间元素的值【大于】要查找的元素，说明要查找的元素在左侧，那么就从左侧按照上述思想继续
  • Java 最长子串、子序列问题 「已注销」 java开发语言后端
    Java算法之最长子串、最长公共子序列、最长公共子串、最长回文串1.无重复字符的最长子串（对应力扣题3）给定一个字符串s，请你找出其中不含有重复字符的最长子串的长度。示例1:输入:s="abcabcbb"输出:3解释:因为无重复字符的最长子串是"abc"，所以其长度为3。可以使用「滑动窗口」来解决这个问题：我们使用两个指针表示字符串中的某个子串（或窗口）的左右边界，其中左指针代表着窗口的左边界「枚
  • 比较好的知识点 hc.Geng java
    2023年Java超全面试题及答案解析---https://blog.csdn.net/qq_42301302/article/details/1287852747分钟带你细致解析4个Java算法必刷题---https://blog.csdn.net/hcxy2022/article/details/12796379750道JAVA基础算法编程题【内含分析、程序答案】---https://blog
  • 完成所有工作的最短时间（Java算法每日一题） 万家林 leetcode算法leetcode
    问：给你一个整数数组jobs，其中jobs[i]是完成第i项工作要花费的时间。请你将这些工作分配给k位工人。所有工作都应该分配给工人，且每项工作只能分配给一位工人。工人的工作时间是完成分配给他们的所有工作花费时间的总和。请你设计一套最佳的工作分配方案，使工人的最大工作时间得以最小化。返回分配方案中尽可能最小的最大工作时间。原题链接：https://leetcode.cn/problems/find
  • Java算法排序之冒泡/插入/选择/快速、二分查找 - 附动图 布衣不才Jerry
    1.Java排序：冒泡排序-最简单（1）比较前后相邻的二个数据，如果前面数据大于后面的数据，就将这二个数据交换。（2）这样对数组的第0个数据到N-1个数据进行一次遍历后，最大的一个数据就“沉”到数组第N-1个位置。（3）N=N-1，如果N不为0就重复前面二步，否则排序完成。Java冒泡排序【逻辑】外层0~array[j+1]){//相邻元素，升序//if(array[j]0;j--){//temp
  • java算法笔记 倔强青铜弟中弟
    排序算法冒泡排序冒泡排序是最简单的排序之一了，其大体思想就是通过与相邻元素的比较和交换来把小的数交换到最前面。这个过程类似于水泡向上升一样，因此而得名。举个栗子：对5,3,8,6,4这个无序序列进行冒泡排序。1.首先从后向前冒泡，4和6比较，把4交换到前面，序列变成5,3,8,4,6。2.同理4和8交换，变成5,3,4,8,6,3和4无需交换。3.5和3交换，变成3,5,4,8,6,3.这样一次冒
  • 华为OD机试 - 数组去重和排序（Java） 程序员阿甘 Java华为OD机试AB卷华为odjava算法
    题目描述给定一个乱序的数组，删除所有的重复元素，使得每个元素只出现一次，并且按照出现的次数从高到低进行排序，相同出现次数按照第一次出现顺序进行先后排序。输入描述一个数组输出描述去重排序后的数组用例输入1,3,3,3,2,4,4,4,5输出3,4,1,2,5备注数组大小不超过100数组元素值大小不超过100。题目解析简单的排序问题。Java算法源码importjava.util.HashMap;im
  • CISC 223 java算法分析 后端
    CISC223-Assignment2(Winter2024)Due:ThursdayFebruary8,2:00PMRegulationsonassignments•Theassignmentsaregradedaccordingtothecorrectness,precisenessandlegibilityofthesolutions.Allhandwrittenparts,includin
  • Java算法练习4 It_张 算法练习Javajava算法开发语言
    Java算法练习41.1[145.二叉树的后序遍历](https://leetcode.cn/problems/binary-tree-postorder-traversal/)1.2[173.二叉搜索树迭代器](https://leetcode.cn/problems/binary-search-tree-iterator/)1.3[98.验证二叉搜索树](https://leetcode.cn
  • Java算法 leetcode简单刷题记录11 程序媛一枚~ JAVA算法算法javaleetcode
    Java算法leetcode简单刷题记录11删除排序链表中的重复元素：https://leetcode.cn/problems/remove-duplicates-from-sorted-list/合并俩个有序数组：https://leetcode.cn/problems/merge-sorted-array/int[]数组转List:Arrays.stream(arr).collect(Coll
  • LeetCode题解java算法： 83. 删除排序链表中的重复元素 神石石 Leecode数据结构和算法链表leetcodejava算法数据结构
    存在一个按升序排列的链表，给你这个链表的头节点head，请你删除所有重复的元素，使每个元素只出现一次。返回同样按升序排列的结果链表。示例1：输入：head=[1,1,2]输出：[1,2]示例2：输入：head=[1,1,2,3,3]输出：[1,2,3]链表解题思路：/***Definitionforsingly-linkedlist.*publicclassListNode{*intval;*Li
  • Java算法 leetcode简单【树的遍历，深度计算及比较】刷题记录 程序媛一枚~ JAVA算法算法javaleetcode
    Java算法leetcode简单【树的遍历，深度计算及比较】刷题记录俩数之和：https://leetcode.cn/problems/two-sum/二进制求和：https://leetcode.cn/problems/add-binary/classSolution{publicStringaddBinary(Stringa,Stringb){intnumA=a.length();intnum
  • 2024年Java实战面试题 内卷成仙 2024年Java面试题java面试springcloud开发语言Java面试题
    高阶篇：2024年Java高阶面试题-CSDN博客算法篇：2024年Java算法面试题-CSDN博客基础篇：2024年Java基础面试题-CSDN博客原理篇：2024年Java原理面试题-CSDN博客搭建篇：2024年Java搭建面试题-CSDN博客
  • 2024年Java算法面试题 内卷成仙 2024年Java面试题算法java排序算法Java面试题
    2024年Java实战面试题（北京）_java5年面试-CSDN博客一、波菲那契递归System.out.println("banc="+banc(10))publicstaticintbanc(intn){if(n==0){return0;}elseif(n==1){return1;}else{returnbanc(n-1)+banc(n-2);}}二、冒泡排序publicstaticvoids
  • Java算法 leetcode简单刷题记录9 程序媛一枚~ JAVA算法算法javaleetcode
    Java算法leetcode简单刷题记录9购买俩块巧克力：https://leetcode.cn/problems/buy-two-chocolates/给定数组量并不大，因此也可以不用PriorityQueue，每次输出最小值；可以暴力循环classSolution{publicintbuyChoco(int[]prices,intmoney){intsum=Integer.MAX_VALUE;
  • Java算法 leetcode简单刷题记录8 程序媛一枚~ JAVA算法算法javaleetcode
    Java算法leetcode简单刷题记录8找出不同元素数目差数组：https://leetcode.cn/problems/find-the-distinct-difference-array/保龄球游戏的获胜者：https://leetcode.cn/problems/determine-the-winner-of-a-bowling-game/计数器II：https://leetcode.cn
  • Java算法 leetcode简单刷题记录10 程序媛一枚~ JAVA算法算法javaleetcode
    Java算法leetcode简单刷题记录10庆祝一下：大概花费了9天，我把所有leetcodeJava的简单题都刷完了，接下来开始冲刺中等和复杂；简单题里用到的比较多的是字符串的处理，转换，拆分，替换，PriorityQueue依次输出最大最小值；走楼梯等动态规划；charAtstartsWithtoLowerCase()replaceAllsplitindexOf进制转换：Integer.val
  • Java算法---递归算法基础介绍 菜到极致就是渣 Java算法算法java
    目录一、递归算法二、递归算法的典型例子（1）阶乘（2）二分查找（3）冒泡排序（4）插入排序一、递归算法计算机科学中，递归是一种解决计算问题的方法。其中解决方案取决于同一类问题的更小子集。说明如下。（1）自己调用自己，如果说每个函数对应着一种解决方案，自己调用自己意味着解决方案是一样的（有规律的）（2）每次调用，函数处理的数据会较上次缩减（子集），而且最后会缩减至无须继续递归。（3）内层函数调用（子
  • java算法之简单的矩阵螺旋式遍历Spiral Matrix Tomes_V_White java算法
    转载自：http://blog.csdn.net/ylyg050518/article/details/48547619继续看一个与数组操作相关的算法，这道题目给我们提供了一个遍历二维数组的新方式——螺旋式遍历。问题描述原文：Givenamatrixofm×nelements(mrows,ncolumns),returnallelementsofthematrixinspiralorder.For
  • Java算法练习题 wsrfsg Java算法练习java算法数据结构动态规划
    目录有效的数独单词拆分动态规划题型dp难点如果想要将列表中的所有字符串连接成一个单一的字符串，可以使用stream().collect()和joining()方法获取列表中的第一个字符串有效的数独publicclassIsShuDu{publicbooleanisValiduku(char[][]board){boolean[][]rowUsed=newboolean[9][9];boolean[
  • Java算法 leetcode简单刷题记录6 程序媛一枚~ JAVA算法算法javaleetcode
    Java算法leetcode简单刷题记录6环和杆：https://leetcode.cn/problems/rings-and-rods/统计范围内的元音字符串数：https://leetcode.cn/problems/count-the-number-of-vowel-strings-in-range/最长平衡子字符串：https://leetcode.cn/problems/find-the
  • Java算法 leetcode简单刷题记录7 程序媛一枚~ 算法JAVA算法javaleetcode
    Java算法leetcode简单刷题记录7最长奇偶子数组：https://leetcode.cn/problems/longest-even-odd-subarray-with-threshold/有的题看着不难，根据提示往下写，有的case就是死活过不了这道题耗了挺久…classSolution{publicintlongestAlternatingSubarray(int[]nums,intt
  • 辗转相处求最大公约数 沐刃青蛟 C++漏洞
    无言面对”江东父老“了，接触编程一年了，今天发现还不会辗转相除法求最大公约数。惭愧惭愧！   为此，总结一下以方便日后忘了好查找。   1.输入要比较的两个数a,b   忽略：2.比较大小（因为后面要的是大的数对小的数做%操作）   3.辗转相除（用循环不停的取余，如a%b,直至b=0）   4.最后的a为两数的最大公约数 &
  • F5负载均衡会话保持技术及原理技术白皮书 bijian1013 F5负载均衡
    一.什么是会话保持？        在大多数电子商务的应用系统或者需要进行用户身份认证的在线系统中，一个客户与服务器经常经过好几次的交互过程才能完成一笔交易或者是一个请求的完成。由于这几次交互过程是密切相关的，服务器在进行这些交互过程的某一个交互步骤时，往往需要了解上一次交互过程的处理结果，或者上几步的交互过程结果，服务器进行下
  • Object.equals方法：重载还是覆盖 Cwind javagenericsoverrideoverload
    本文译自StackOverflow上对此问题的讨论。 原问题链接   在阅读Joshua Bloch的《Effective Java（第二版）》第8条“覆盖equals时请遵守通用约定”时对如下论述有疑问： “不要将equals声明中的Object对象替换为其他的类型。程序员编写出下面这样的equals方法并不鲜见，这会使程序员花上数个小时都搞不清它为什么不能正常工作：” pu
  • 初始线程 15700786134
          暑假学习的第一课是讲线程，任务是是界面上的一条线运动起来。            既然是在界面上，那必定得先有一个界面，所以第一步就是，自己的类继承JAVA中的JFrame，在新建的类中写一个界面，代码如下： public class ShapeFr
  • Linux的tcpdump 被触发 tcpdump
    用简单的话来定义tcpdump，就是：dump the traffic on a network，根据使用者的定义对网络上的数据包进行截获的包分析工具。 tcpdump可以将网络中传送的数据包的“头”完全截获下来提供分析。它支 持针对网络层、协议、主机、网络或端口的过滤，并提供and、or、not等逻辑语句来帮助你去掉无用的信息。 实用命令实例 默认启动 tcpdump 普通情况下，直
  • 安卓程序listview优化后还是卡顿 肆无忌惮_ ListView
    最近用eclipse开发一个安卓app，listview使用baseadapter，里面有一个ImageView和两个TextView。使用了Holder内部类进行优化了还是很卡顿。后来发现是图片资源的问题。把一张分辨率高的图片放在了drawable-mdpi文件夹下，当我在每个item中显示，他都要进行缩放，导致很卡顿。解决办法是把这个高分辨率图片放到drawable-xxhdpi下。 &nb
  • 扩展easyUI tab控件，添加加载遮罩效果 知了ing jquery
    (function () { $.extend($.fn.tabs.methods, { //显示遮罩 loading: function (jq, msg) { return jq.each(function () { var panel = $(this).tabs(&
  • gradle上传jar到nexus 矮蛋蛋 gradle
    原文地址： https://docs.gradle.org/current/userguide/maven_plugin.html configurations {     deployerJars } dependencies {     deployerJars "org.apache.maven.wagon
  • 千万条数据外网导入数据库的解决方案。 alleni123 sqlmysql
    从某网上爬了数千万的数据，存在文本中。 然后要导入mysql数据库。 悲剧的是数据库和我存数据的服务器不在一个内网里面。。 ping了一下， 19ms的延迟。 于是下面的代码是没用的。 ps = con.prepareStatement(sql); ps.setString(1, info.getYear())............; ps.exec
  • JAVA IO InputStreamReader和OutputStreamReader 百合不是茶 JAVA.io操作 字符流
    这是第三篇关于java.io的文章了，从开始对io的不了解-->熟悉--->模糊，是这几天来对文件操作中最大的感受，本来自己认为的熟悉了的，刚刚在回想起前面学的好像又不是很清晰了，模糊对我现在或许是最好的鼓励 我会更加的去学 加油！： JAVA的API提供了另外一种数据保存途径，使用字符流来保存的，字符流只能保存字符形式的流   字节流和字符的难点：a,怎么将读到的数据
  • MO、MT解读 bijian1013 GSM
    MO= Mobile originate，上行，即用户上发给SP的信息。MT= Mobile Terminate，下行，即SP端下发给用户的信息； 上行:mo提交短信到短信中心下行:mt短信中心向特定的用户转发短信，你的短信是这样的，你所提交的短信，投递的地址是短信中心。短信中心收到你的短信后，存储转发，转发的时候就会根据你填写的接收方号码寻找路由，下发。在彩信领域是一样的道理。下行业务：由SP
  • 五个JavaScript基础问题 bijian1013 JavaScriptcallapplythisHoisting
    下面是五个关于前端相关的基础问题，但却很能体现JavaScript的基本功底。 问题1：Scope作用范围 考虑下面的代码：  (function() { var a = b = 5; })(); console.log(b); 什么会被打印在控制台上？  回答：         上面的代码会打印 5。 &nbs
  • 【Thrift二】Thrift Hello World bit1129 Hello world
    本篇，不考虑细节问题和为什么，先照葫芦画瓢写一个Thrift版本的Hello World，了解Thrift RPC服务开发的基本流程   1. 在Intellij中创建一个Maven模块，加入对Thrift的依赖，同时还要加上slf4j依赖，如果不加slf4j依赖，在后面启动Thrift Server时会报错 <dependency>
  • 【Avro一】Avro入门 bit1129 入门
    本文的目的主要是总结下基于Avro Schema代码生成，然后进行序列化和反序列化开发的基本流程。需要指出的是，Avro并不要求一定得根据Schema文件生成代码，这对于动态类型语言很有用。   1. 添加Maven依赖   <?xml version="1.0" encoding="UTF-8"?> <proj
  • 安装nginx+ngx_lua支持WAF防护功能 ronin47
    需要的软件:LuaJIT-2.0.0.tar.gz                   nginx-1.4.4.tar.gz          &nb
  • java-5.查找最小的K个元素-使用最大堆 bylijinnan java
    import java.util.Arrays; import java.util.Random; public class MinKElement { /** * 5.最小的K个元素 * I would like to use MaxHeap. * using QuickSort is also OK */ public static void
  • TCP的TIME-WAIT bylijinnan socket
    原文连接： http://vincent.bernat.im/en/blog/2014-tcp-time-wait-state-linux.html 以下为对原文的阅读笔记 说明： 主动关闭的一方称为local end，被动关闭的一方称为remote end 本地IP、本地端口、远端IP、远端端口这一“四元组”称为quadruplet，也称为socket 1、TIME_WA
  • jquery ajax 序列化表单 coder_xpf Jquery ajax 序列化
       checkbox 如果不设定值，默认选中值为on；设定值之后，选中则为设定的值   <input type="checkbox" name="favor" id="favor" checked="checked"/> $("#favor&quo
  • Apache集群乱码和最高并发控制 cuisuqiang apachetomcat并发集群乱码
    都知道如果使用Http访问，那么在Connector中增加URIEncoding即可，其实使用AJP时也一样，增加useBodyEncodingForURI和URIEncoding即可。 最大连接数也是一样的，增加maxThreads属性即可，如下，配置如下： <Connector maxThreads="300" port="8019" prot
  • websocket dalan_123 websocket
    一、低延迟的客户端-服务器 和 服务器-客户端的连接 很多时候所谓的http的请求、响应的模式，都是客户端加载一个网页，直到用户在进行下一次点击的时候，什么都不会发生。并且所有的http的通信都是客户端控制的，这时候就需要用户的互动或定期轮训的，以便从服务器端加载新的数据。   通常采用的技术比如推送和comet（使用http长连接、无需安装浏览器安装插件的两种方式：基于ajax的长
  • 菜鸟分析网络执法官 dcj3sjt126com 网络
      最近在论坛上看到很多贴子在讨论网络执法官的问题。菜鸟我正好知道这回事情.人道"人之患好为人师" 手里忍不住,就写点东西吧. 我也很忙.又没有MM,又没有MONEY....晕倒有点跑题. OK,闲话少说,切如正题. 要了解网络执法官的原理. 就要先了解局域网的通信的原理. 前面我们看到了.在以太网上传输的都是具有以太网头的数据包. 
  • Android相对布局属性全集 dcj3sjt126com android
    RelativeLayout布局android:layout_marginTop="25dip" //顶部距离android:gravity="left" //空间布局位置android:layout_marginLeft="15dip //距离左边距 // 相对于给定ID控件android:layout_above 将该控件的底部置于给定ID的
  • Tomcat内存设置详解 eksliang jvmtomcattomcat内存设置
    Java内存溢出详解   一、常见的Java内存溢出有以下三种：   1. java.lang.OutOfMemoryError: Java heap space ----JVM Heap（堆）溢出JVM在启动的时候会自动设置JVM Heap的值，其初始空间(即-Xms)是物理内存的1/64，最大空间(-Xmx)不可超过物理内存。 可以利用JVM提
  • Java6 JVM参数选项 greatwqs javaHotSpotjvmjvm参数JVM Options
    Java 6 JVM参数选项大全（中文版）   作者：Ken Wu Email: [email protected] 转载本文档请注明原文链接 http://kenwublog.com/docs/java6-jvm-options-chinese-edition.htm！   本文是基于最新的SUN官方文档Java SE 6 Hotspot VM Opt
  • weblogic创建JMC i5land weblogicjms
    进入 weblogic控制太 1.创建持久化存储 --Services--Persistant Stores--new--Create FileStores--name随便起--target默认--Directory写入在本机建立的文件夹的路径--ok 2.创建JMS服务器 --Services--Messaging--JMS Servers--new--name随便起--Pers
  • 基于 DHT 网络的磁力链接和BT种子的搜索引擎架构 justjavac DHT
    上周开发了一个磁力链接和 BT 种子的搜索引擎 {Magnet & Torrent}，本文简单介绍一下主要的系统功能和用到的技术。 系统包括几个独立的部分： 使用 Python 的 Scrapy 框架开发的网络爬虫，用来爬取磁力链接和种子； 使用 PHP CI 框架开发的简易网站； 搜索引擎目前直接使用的 MySQL，将来可以考虑使
  • sql添加、删除表中的列 macroli sql
    添加没有默认值：alter table Test add BazaarType char(1) 有默认值的添加列：alter table Test add BazaarType char(1) default(0) 删除没有默认值的列：alter table Test drop COLUMN BazaarType 删除有默认值的列：先删除约束（默认值）alter table Test DRO
  • PHP中二维数组的排序方法 abc123456789cba 排序二维数组PHP
    <?php/*** @package     BugFree* @version     $Id: FunctionsMain.inc.php,v 1.32 2005/09/24 11:38:37 wwccss Exp $*** Sort an two-dimension array by some level
  • hive优化之------控制hive任务中的map数和reduce数 superlxw1234 hivehive优化
    一、    控制hive任务中的map数: 1.    通常情况下，作业会通过input的目录产生一个或者多个map任务。 主要的决定因素有： input的文件总个数，input的文件大小，集群设置的文件块大小(目前为128M, 可在hive中通过set dfs.block.size;命令查看到，该参数不能自定义修改)；2. 
  • Spring Boot 1.2.4 发布 wiselyman spring boot
    Spring Boot 1.2.4已于6.4日发布，repo.spring.io and Maven Central可以下载(推荐使用maven或者gradle构建下载)。   这是一个维护版本，包含了一些修复small number of fixes,建议所有的用户升级。   Spring Boot 1.3的第一个里程碑版本将在几天后发布，包含许多
按字母分类： ABCDEFGHIJKLMNOPQRSTUVWXYZ其他