Python计算机视觉第三章 图像映射
原理
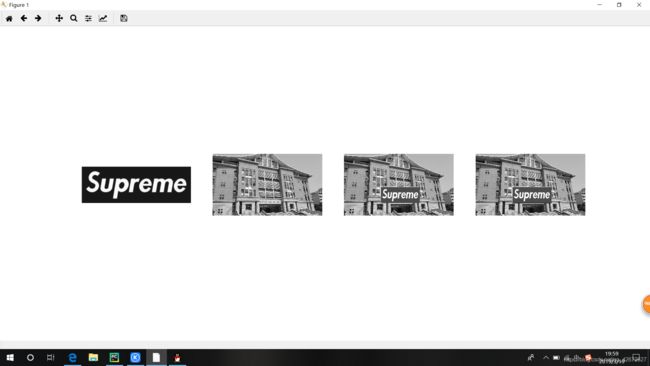
仿射扭曲的一个简单例子是将图像或者图像的一部分放置到另一幅图像中。函数输入两幅图像和一个坐标。其中tp是设置将第一幅图像放置到第二幅图像中的角点坐标。前面4个数字[a1,a2,a3,a4]代表角点的纵坐标,后面4个数[b1,b2,b3,b4]为横坐标,从左上角为第一个角点逆时针下去,即[a1,b1]为左上角点坐标,[a2,b2]为左下角点坐标,以此类推。最后面全为1的是α通道,将该图片所在的位置全部设为1(即可以通过)。函数Haffine_from_point()会返回给定点对应点对的最优仿射变换,用fp与tp比较。在例子中,对应点对为图像和建筑物的角点。在透视效应比较弱,那么这种方法会返回很好的结果。
附Alpha 通道定义:一个图像的每个像素都有 RGB 三个通道,后来 Alvy Ray Smith 提出每个像素再增加一个 Alpha 通道,取值为0到1,用来储存这个像素是否对图片有「贡献」,0代表透明、1代表不透明。
代码
from PCV.geometry import warp, homography
from PIL import Image
from pylab import *
from scipy import ndimage
im1 = array(Image.open('s.jpg').convert('L'))
im2 = array(Image.open('7.jpg').convert('L'))
tp = array([[120,260,260,120],[500,500,730,730],[1,1,1,1]])
#tp = array([[675,826,826,677],[55,52,281,277],[1,1,1,1]])
im3 = warp.image_in_image(im1,im2,tp)
figure()
gray()
subplot(141)
axis('off')
imshow(im1)
subplot(142)
axis('off')
imshow(im2)
subplot(143)
axis('off')
imshow(im3)
m,n = im1.shape[:2]
fp = array([[0,m,m,0],[0,0,n,n],[1,1,1,1]])
tp2 = tp[:,:3]
fp2 = fp[:,:3]
H = homography.Haffine_from_points(tp2,fp2)
im1_t = ndimage.affine_transform(im1,H[:2,:2],
(H[0,2],H[1,2]),im2.shape[:2])
alpha = warp.alpha_for_triangle(tp2,im2.shape[0],im2.shape[1])
im3 = (1-alpha)*im2 + alpha*im1_t
tp2 = tp[:,[0,2,3]]
fp2 = fp[:,[0,2,3]]
H = homography.Haffine_from_points(tp2,fp2)
im1_t = ndimage.affine_transform(im1,H[:2,:2],
(H[0,2],H[1,2]),im2.shape[:2])
alpha = warp.alpha_for_triangle(tp2,im2.shape[0],im2.shape[1])
im4 = (1-alpha)*im3 + alpha*im1_t
subplot(144)
imshow(im4)
axis('off')
show()