Python中如何利用经纬度进行距离计算

前些天由于工作中需求，要计算经纬度之间的距离，当我去网上搜索距离计算的方法时，发现很多文章中的方法乍一看都是很不同的，同是进行距离计算，为啥这么不一样呢？后来才发现问题在于很多文章没有进行相关的原理说明，直接上了一段代码，让人看了云里雾里的。

其实经纬度属于球面坐标，而我们常规的距离是在平面维度上的，因此，在进行距离计算之前，首先需将球面坐标转换为平面坐标，这样之后才能进行平面距离的测算，计算出来的距离单位就是米了，符合我们的常规认知。（我之前查到的一些方法中，有些是直接调包，有些是十进制和弧度互相做转换，初次接触时可能不是那么好理解背后原理）

以下是亲身实践后，总结的一些可行的计算方法。

一、这种方法按照以上原理，一步一步进行。即先做坐标转换，再进行平面距离计算。
1、这里的坐标转换，可以使用pyproj包中的Transformer功能，以下是代码：

def axis_conversion(data,lat,lon):
    #注意lat 在前，lon在后，不能写反
    lon = data[lon].values
    lat = data[lat].values
    transformer = Transformer.from_crs("epsg:4326", "epsg:3857")
    #这里将epsg4326转换为epsg3857
    #关于坐标系的知识可以参考这个网址：https://www.cnblogs.com/E7868A/p/11460865.html
    x3, y3 = transformer.transform(lat, lon)
    return (x3,y3)

2、坐标转换完成后，套用欧氏距离计算公式，来进行距离的测算。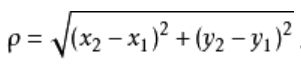
二、直接使用python中现有包的功能（推荐）。
这里的包指的是scipy，scipy是一个高级的科学计算库，常见的是插值运算、优化算法、图像处理和数学统计等。它用于有效计算Numpy矩阵，使Numpy和Scipy协同工作，高效解决问题。
这里使用到的是scipy.spatial子模块，具体使用方式如下：

from scipy.spatial.distance import cdist
lonlat1=data_lonlat_1[['lat_1','lon_1']]       
lonlat2=data_lonlat_2[['lat_2','lon_2']]
distance=cdist(lonlat1,lonlat2,metric='euclidean')

不得不说，方法二真的很强大了！对比方法一会高效很多，当数据量大的时候尤其明显，更推荐哈（两种方法的结果是一致的）。

三、其他
在资料搜索过程中，也有看到另外两种方法，我目前没有真正使用，但是测试过，与上面两种方法得出的结果，会稍有偏差，感兴趣的可以研究下。

from geopy.distance import geodesic
print(geodesic((lat1,lon1), (lat2,lon2)).m)

from math import radians, cos, sin, asin, sqrt
def distance_between_points(lat1, lon1, lat2, lon2):
    """
    Calculate the great circle distance between two points
    on the earth (specified in decimal degrees)
    """
    # 将十进制度数转化为弧度
    lon1, lat1, lon2, lat2 = map(radians, [float(lon1), float(lat1), float(lon2), float(lat2)])
    # haversine 公式
    dlon = lon2 - lon1
    dlat = lat2 - lat1
    a = sin(dlat / 2) ** 2 + cos(lat1) * cos(lat2) * sin(dlon / 2) ** 2
    c = 2 * asin(sqrt(a))
    r = 6371  # 地球平均半径，单位为公里
    return c * r * 1000  

如果这篇文章对你有帮助，请帮忙点点赞哦~