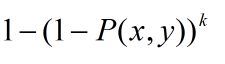福州大学第十四届程序设计竞赛-重现赛（Record）
Accept: 108 Submit: 400
Time Limit: 1000 mSec Memory Limit : 32768 KB
Problem Description
海边躺着一排咸鱼，一些有梦想的咸鱼成功翻身（然而没有什么卵用），一些则是继续当咸鱼。一个善良的渔夫想要帮这些咸鱼翻身，但是渔夫比较懒，所以只会从某只咸鱼开始，往一个方向，一只只咸鱼翻过去，翻转若干只后就转身离去，深藏功与名。更准确地说，渔夫会选择一个区间[L,R]，改变区间内所有咸鱼的状态，至少翻转一只咸鱼。
渔夫离开后想知道如果他采取最优策略，最多有多少只咸鱼成功翻身，但是咸鱼大概有十万条，所以这个问题就交给你了！
Input
包含多组测试数据。
每组测试数据的第一行为正整数n，表示咸鱼的数量。
第二行为长n的01串，0表示没有翻身，1表示成功翻身。
n≤100000
Output
在渔夫的操作后，成功翻身咸鱼（即1）的最大数量。
Sample Input
Sample Output
类似于最大连续子序列
dp[x]：前x个鱼最多能翻出多少条
如果第i个数为0，那么dp[i] = dp[i-1]+1，否则dp[i] = max(dp[i-1]-1, 0)
最后答案再加上1的数量，注意如果全为1的时候因为必须要翻所以答案是n-1，坑
#include
#include
#include
using namespace std;
int a[100005], dp[100005];
int main(void)
{
int n, i, ans, temp;
while(scanf("%d", &n)!=EOF)
{
temp = ans = 0;
memset(dp, 0, sizeof(dp));
for(i=1;i<=n;i++)
{
scanf("%d", &a[i]);
if(a[i]==0)
dp[i] = dp[i-1]+1;
else
{
temp++;
dp[i] = max(dp[i-1]-1, 0);
}
ans = max(ans, dp[i]);
}
if(temp==n)
printf("%d\n", temp-1);
else
printf("%d\n", ans+temp);
}
return 0;
}
Accept: 33 Submit: 188
Time Limit: 1000 mSec Memory Limit : 32768 KB
Problem Description
在过三个礼拜，YellowStar有一场专业英语考试，因此它必须着手开始复习。
这天，YellowStar准备了n个需要背的单词，每个单词的长度均为m。
YellowSatr准备采用联想记忆法来背诵这n个单词：
1、如果YellowStar凭空背下一个新词T，需要消耗单词长度m的精力
2、如果YellowSatr之前已经背诵了一些单词，它可以选择其中一个单词Si，然后通过联想记忆的方法去背诵新词T，需要消耗的精力为hamming(Si, T) * w。
hamming(Si, T)指的是字符串Si与T的汉明距离，它表示两个等长字符串之间的汉明距离是两个字符串对应位置的不同字符的个数。
由于YellowStar还有大量繁重的行政工作，因此它想消耗最少的精力背诵下这n个单词，请问它最少需要消耗多少精力。
Input
包含多组测试数据。
第一行为n, m, w。
接下来n个字符串，每个字符串长度为m，每个单词均为小写字母'a'-'z'组成。
1≤n≤1000
1≤m, w≤10
Output
输出一个值表示答案。
Sample Input
Sample Output
就是个最小生成树嘛，任意两个单词之间都连一条长度为hamming(Si, T)*w的边，
然后新建一个点，所有的单词都向这个点连一条长度为m的边
最后求这个图的最小生成树就好了，模板模板
#include
#include
#include
#include
char str[1005][15];
int road[1005][1005], flag[1005], bet[1005], sum;
int CreatMST(int n);
int main()
{
int n, m, w, i, j, k, cot;
while(scanf("%d%d%d", &n, &m, &w)!=EOF)
{
n += 1;
memset(road, 88, sizeof(road));
for(i=2;i<=n;i++)
{
scanf("%s", str[i]+1);
road[1][i] = road[i][1] = m;
}
for(i=2;i<=n;i++)
{
for(j=2;j<=n;j++)
{
if(i==j)
continue;
cot = 0;
for(k=1;k<=m;k++)
{
if(str[i][k]!=str[j][k])
cot++;
}
road[i][j] = road[j][i] = cot*w;
}
}
sum = 0;
memset(flag, 0, sizeof(flag));
printf("%d\n", CreatMST(n));
}
return 0;
}
int CreatMST(int n)
{
int i, j, x, k;
flag[1] = 1;
for(i=2;i<=n;i++)
bet[i] = road[1][i];
for(i=2;i<=n;i++)
{
k = INT_MAX, x = 2;
for(j=2;j<=n;j++)
{
if(flag[j]==0 && bet[j] C：过河
没写，感觉还是个dp，dp[k][a][b]表示已经开了k次船当前岸边还剩下a和Y星人和b个S星人的情况个数
不知道这样行不行，时间不够先溜了
Accept: 58 Submit: 221
Time Limit: 1500 mSec Memory Limit : 32768 KB
Problem Description
某一天，YellowStar在人生的道路上迷失了方向，迷迷糊糊之中，它误入了一座迷宫中，幸运的是它在路口处发现了一张迷宫的地图。
经过它的观察，它发现这个迷宫一共有n个房间，并且这n个房间呈现一个有根树结构，它现在所在的1号房间为根，其它每个房间都有一个上级房间，连接第i个房间和它的上级房间Pi的道路长度为Wi。
在地图的背面，记载了这个迷宫中，每个房间拥有一个时空传送门，第i个房间的传送门可以花费Di单位的时间传送到它的任意一个下级房间中（如果x是y的下级房间，并且y是z的下级房间，那么x也是z的下级房间）。
YellowStar的步行速度为1单位时间走1长度，它现在想知道从1号房间出发，到每一个房间的最少时间。
Input
包含多组测试数据。
第一行输入n表示n个房间。
第二行输出n个数字，第i个数字Di表示i号房间传送器需要花费的时间。
接下来n-1行，第i行包含两个数字Pi和Wi，表示i+1号房间的上级房间为Pi，道路长度为Wi。
1≤n≤100000
1≤Di, Wi≤10^9
Output
输出n个数，第i个数表示从1号房间出发到i号房间的最少时间。 (注意，输出最后一个数字后面也要加一个空格)
Sample Input
Sample Output
很简单的树形dp
从根往下搜，dp[x]表示到达x节点的最小时间，每次传入所有祖宗中最dp[i]+D[i]最小的那个和直接移动作对比
#include
#include
#include
using namespace std;
#define LL long long
vector G[100005];
int fly[100005], len[100005];
LL dp[100005];
void Sech(int u, int p, LL bet)
{
int v, i;
for(i=0;i
Accept: 8 Submit: 39
Time Limit: 1000 mSec Memory Limit : 32768 KB
Problem Description
Saya最近喜欢上了小熊饼干，但是他有非常严重的选择困难症，当然面对这一堆小熊饼干的时候，想起了一句至理名言“犹豫不决么？ 那就来RAND()一下吧！”。
于是，Saya把小熊饼干排成了一个N*M的矩阵，每个位置上都放着一块小熊饼干。每当他想吃小熊饼干的时候，他就运行一下代码。（random()为生成一个任意正整数）。
x1=random() mod N+1;
y1=random() mod M+1;
x2=random() mod N+1;
y2=random() mod M+1;
然后将以(x1, y1)，(x2, y2)为两个顶点的，四条边平行于边界的一个子矩形内的小熊饼干全部吃掉（两个点的连线为矩形的对角线，如果x1=x2或者y1=y2，则认为矩形的长度或宽度为1）。显然，如果某个位置上的小熊饼干已经被吃掉了，那Saya就什么都吃不到了。
在这题中，我们假定random()函数非常完美，得到每个格子的概率相等。
请你帮忙算一算，K次之内她期望可以吃到块小熊饼干？
Input
包含多组测试数据。
一行内包括三个正整数K，N，M。
0≤K≤10000，1≤N，M≤1000
Output
一个整数，K次之内期望可以吃到的小熊饼干块数（四舍五入精确到整数）。
Sample Input
Sample Output
求出每个格子小熊饼干被吃掉的概率，然后相加就是答案了
对于格子(x, y)上的小熊饼干，在一次随机时被选中的概率
因为要随机k次，那么随机k次后被选中的概率就为（k过大快速幂吧）
最后全部加在一起就好了
#include
double Pow(double x, int k)
{
double ans = 1;
while(k)
{
if(k%2==1)
ans = ans*x;
x = x*x;
k /= 2;
}
return ans;
}
int main(void)
{
int k, n, m, i, j;
double ans;
while(scanf("%d%d%d", &k, &n, &m)!=EOF)
{
ans = 0;
for(i=1;i<=n;i++)
{
for(j=1;j<=m;j++)
ans += 1-Pow(1-((2.0*i*(n-i+1)-1)/(n*n))*((2.0*j*(m-j+1)-1)/(m*m)), k);
}
printf("%.0f\n", ans);
}
return 0;
}
Accept: 139 Submit: 712
Time Limit: 2000 mSec Memory Limit : 32768 KB
Problem Description
福州大学某班共有n名学生，这些学生这学期都选修了3门课，分别是大物、高数、大英。YellowStar想对这学期总绩点不低于3.0的学生进行奖励，所以他将每名学生每门课程的分数告诉你，并希望你能告诉他他必须对多少名学生进行奖励。
对于单门课程的绩点计算方法是(分数/10-5)，如分数是69，那么绩点就是1.9，学生的总绩点就是他每门课程的绩点的平均值。但是要注意的是，当某门课程的分数小于60时，就会被视为挂科，总绩点直接为0。
Input
包含多组测试数据。
第一行输入一个整数n，表示一共有n名学生。
接下来输入n行，每行3个整数，分别表示当前学生的3门课程的分数，分数都不大于100且不小于0。
n≤500000
Output
输出一个整数，表示有多少人的总绩点不低于3.0。
Sample Input
Sample Output
水题，但卡double，需要用int
#include
int main(void)
{
int n, i, sum, a, b, c, s;
while(scanf("%d", &n)!=EOF)
{
sum = 0;
for(i=1;i<=n;i++)
{
scanf("%d%d%d", &a, &b, &c);
if(a<60 || b<60 || c<60)
continue;
s = a+b+c-150;
if(s>=90)
sum++;
}
printf("%d\n", sum);
}
return 0;
} 感觉上是找出所有的奇环，然后看这所有的奇环是否有公共边，没有方案数就为0，否则就是公共边的个数
不会写，溜了溜了
Accept: 8 Submit: 108
Time Limit: 3000 mSec Memory Limit : 32768 KB
Problem Description
有如下取牌游戏：
1. 桌面上有n张卡牌从左到右排成一行，每张卡牌上有一个数字；
2. 游戏按轮次进行，每一轮中取掉所有比左边数值小的卡牌；
3. 当无牌可取的时候则游戏结束。
比如初始卡牌为{5, 6, 3, 7, 4, 1, 2}，共需2轮取牌。取牌过程如下（小括号为每轮取掉的牌）：
{5, 6, 3, 7, 4, 1, 2}
==> {5, 6, (3), 7, (4), (1), 2}
==> {5, 6, 7, 2}
==> {5, 6, 7, (2)}
==> {5, 6, 7}
现按顺序给定初始的卡牌数字，请求出游戏结束时取牌的总轮次，并输出结束时桌上剩余的卡牌序列。
Input
包含多组测试数据。
输入包含两行。
第一行包含一个整数n表示卡牌的数量。
第二行包含n个空格隔开的整数，表示排成一行的卡牌上对应的数字(取值范围[1,1000000000])。
n≤1000000
Output
输出包含两行。
第一行包含一个整数表示游戏的取牌总轮次。
第二行包含游戏结束时桌上剩余的卡牌序列，用空格隔开。
Sample Input
Sample Output
剩余的卡牌很好求，问题要消多少次
样例不够强
再加两组自己的吧
第一行答案应该是3和5
单调栈+dp（为什么感觉每题都要dp一下）
对于当前第i个数，如果栈顶元素小于等于它，那么弹出栈顶元素，直到栈为空或者栈顶元素大于它
弹出时分两种情况：
①如果当前栈内只有一个元素了，那么这个元素一定是最后消不掉的！不管，直接把它加入答案
②如果栈内不止一个元素，那么栈顶元素一定是可以消掉的
设栈顶元素是第k个元素（下标为k），那么dp[i] = max(dp[i], dp[k]+1)，
意思就是第i个元素如果可以消掉，那么它一定排在第k个元素被消掉之后
最后所有可消掉元素中最大的dp[i]就是答案
#include
#include
#include
#include
using namespace std;
stack st;
int a[1000005], dp[1000005], rec[1000005];
int main(void)
{
int n, i, ans, k;
while(scanf("%d", &n)!=EOF)
{
if(n==0)
{
printf("0\n\n");
continue;
}
ans = k = 0;
memset(dp, 0, sizeof(dp));
for(i=1;i<=n;i++)
scanf("%d", &a[i]);
for(i=1;i<=n;i++)
{
while(st.empty()==0 && a[st.top()]<=a[i])
{
if(st.size()==1)
{
rec[++k] = a[st.top()];
st.pop();
}
else
{
dp[i] = max(dp[i], dp[st.top()]+1);
ans = max(ans, dp[i]);
st.pop();
}
}
st.push(i);
}
while(st.empty()==0)
{
if(st.size()==1)
{
rec[++k] = a[st.top()];
st.pop();
}
else
{
ans = max(ans, dp[st.top()]+1);
st.pop();
}
}
printf("%d\n%d", ans, rec[1]);
for(i=2;i<=k;i++)
printf(" %d", rec[i]);
printf("\n");
}
return 0;
}
Accept: 87 Submit: 228
Time Limit: 1500 mSec Memory Limit : 32768 KB
Problem Description
TonyY是一个喜欢到处浪的男人，他的梦想是带着兰兰姐姐浪遍天朝的各个角落，不过在此之前，他需要做好规划。
现在他的手上有一份天朝地图，上面有n个城市，m条交通路径，每条交通路径都是单行道。他已经预先规划好了一些点作为旅游的起点和终点，他想选择其中一个起点和一个终点，并找出从起点到终点的一条路线亲身体验浪的过程。但是他时间有限，所以想选择耗时最小的，你能告诉他最小的耗时是多少吗？
Input
包含多组测试数据。
输入第一行包括两个整数n和m，表示有n个地点，m条可行路径。点的编号为1 - n。
接下来m行每行包括三个整数i, j, cost，表示从地点i到地点j需要耗时cost。
接下来一行第一个数为S，表示可能的起点数，之后S个数，表示可能的起点。
接下来一行第一个数为E，表示可能的终点数，之后E个数，表示可能的终点。
0
Output
输出他需要的最短耗时。
Sample Input
Sample Output
裸的最短路
新建两个点a和b
最后求一边从a到b的最短路就好了
#include
#include
#include
#include
#include
using namespace std;
typedef struct
{
int v;
int len;
}Road;
Road temp;
vector G[100005];
queue q;
int in[100005], out[100005], best[100005], vis[100005];
int main(void)
{
int n, m, i, u, v, len, now, ans;
while(scanf("%d%d", &n, &m)!=EOF)
{
for(i=1;i<=n;i++)
G[i].clear();
while(m--)
{
scanf("%d%d%d", &u, &v, &len);
temp.v = v, temp.len = len;
G[u].push_back(temp);
}
memset(in, 0, sizeof(in));
memset(out, 0, sizeof(out));
scanf("%d", &len);
while(len--)
{
scanf("%d", &u);
in[u] = 1;
}
scanf("%d", &len);
while(len--)
{
scanf("%d", &v);
out[v] = 1;
}
memset(best, 62, sizeof(best));
memset(vis, 0, sizeof(vis));
for(i=1;i<=n;i++)
{
if(in[i])
{
best[i] = 0;
q.push(i);
vis[i] = 1;
}
}
while(q.empty()==0)
{
now = q.front();
vis[now] = 0;
q.pop();
for(i=0;i