数据结构之图的存储表示(邻接矩阵、邻接表和边集数组)
图的存储结构相比线性表与树而言,更加复杂。图不可能用简单的顺序存储结构来表示,这是一个很困难的问题。所幸,一般有三种存储结构:邻接矩阵、邻接表和边集数组。
邻接矩阵
邻接矩阵是表示顶点之间相邻关系的矩阵。看图就知道了:
(PS:感谢Covit大佬提供的皂片)
上面的图片演示的是关于带权图,所以里面存储的是权值,如果是无向图的话,一般用1表示有边,0表示无边。
从图的邻接矩阵存储方法(或称数组存储法)容翻译看出这种表示具有以下特点。
1、无向图的邻接矩阵一定是对称的;而有向图的邻接矩阵不一定对称。用邻接矩阵来表示一个具有n个顶点的图时需要n²个存储量来存储邻接矩阵。
2、对于无向图,邻接矩阵的第i行非零元素的个数正好是第i个顶点的度TD(Vi)。
3、对于有向图,邻接矩阵的第i行非零元素的个数正好是第i个顶点的出度OD(Vi)(或入度ID(Vi))。
4、邻接矩阵的局限在于很容易确定图中任意两个顶点之间是否有边相连。但是必须按行、列对每个元素进行检测才能够确定图中有多少条边。
show the code
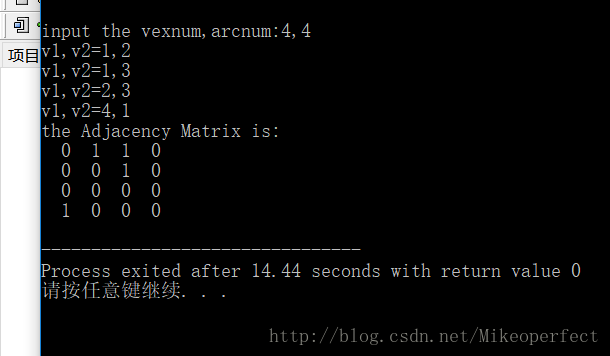
建立一个有向图的邻接矩阵
#includeprintf("v1,v2=");
scanf("%d,%d",&v1,&v2);
cost[v1][v2]=1;
}
return vexnum;
}
int main()
{
int i,j,vexnum;
int cost[max][max];
vexnum=creatcost(cost);
printf("the Adjacency Matrix is:\n");
for(i=1;i<=vexnum;i++)
{
for(j=1;j<=vexnum;j++)
printf("%3d",cost[i][j]);
printf("\n");
}
return 0;
} 运行示例
代码很简单,邻接矩阵确实没有什么难度,值得注意的是在输入数字时记得是在半角输入法状态,以免出现输入流过大而造成程序运行出错的现象。
——————————————————————————————————
邻接表
邻接表(Adjacency List)是图的一种顺序存储与链式存储相结合的存储方式。
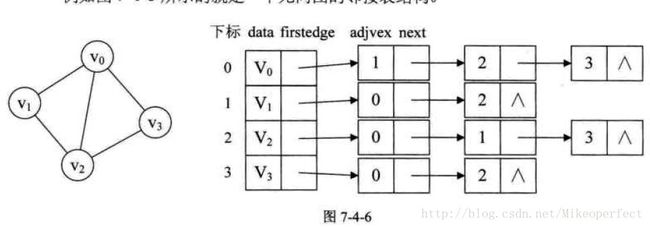
对于图G中的每个顶点Vi,将邻接于Vi的所有顶点Vj链成一个单链表,单链表中的节点称为表节点,这个单链表就称为顶点Vi 的邻接表。
邻接表是由两部分组成的,一部分是头节点:顶点域(vertex)+指针域(firstedge),另一部分是表节点:邻接顶点域(adjvex)+指针域(next)。
注意:
1、 上图的data对应于文中的vertex。
2、一个图的邻接矩阵是唯一的,但其邻接表不是唯一的。因为在邻接表的每一个单链表中,各节点的顺序可以是任意的。通常情况下,为了编程方便而采用头插法。
由邻接表可知,对于无向图,第i个顶点Vi的度,就是i号单链表中节点个数。而在有向图中,i号单链表中的节点个数只是顶点Vi的出度。为了便于确定有向图节点的入度,可以为有向图建立逆邻接表。
邻接表的存储结构
typedef struct node /*定义表节点*/
{
int adjvex;
struct node*next;
}arcnode;
typedef struct vexnode /*定义头节点*/
{
int vertex;
arcnode*firstarc;
}vexnode;
vexnode adjlist[max];完整代码
#includeprintf("v1,v2=");
scanf("%d,%d",&v1,&v2);
ptr=(arcnode*)malloc(sizeof(arcnode));/*核心........*/
ptr->adjvex=v2;
ptr->next=adjlist[v1].firstarc;
adjlist[v1].firstarc=ptr;
ptr=(arcnode*)malloc(sizeof(arcnode));
ptr->adjvex=v1;
ptr->next=adjlist[v2].firstarc;
adjlist[v2].firstarc=ptr; /*..... 核心*/
}
return vexnum;
}
int main()
{
int i,n;
arcnode*p;
n=creatadjlist();
printf("the Adjacency List:\n");
for(i=1;i<=n;i++)
{
printf("%d=>",i);
p=adjlist[i].firstarc;
while(p!=NULL)
{
printf("---->%d",p->adjvex);
p=p->next;
}
putchar('\n');
}
return 0;
} ——————————————————————————
边集数组
带权图(网)的另一种存储结构是边集数组,它适用于一些以边为主的操作。用边集数组表示带权图时,列出每条边所依附的两个顶点及边上的权,即每个数组元素代表一条边的信息。
一个图的边集数组,其形式描述如下:
typedef struct
{
int head,tail;
edgetype data;
}data;
edge edgearray[max];总结
图的存储结构一般以上述三种最为普遍:邻接矩阵,邻接表和边集数组,其中,邻接矩阵和边集数组相对简单,邻接表重点理解其存储结构:头节点和表节点,代码相对来说简单,重点理解其中的核心代码部分,其中的核心代码部分采用的是头插法,但这个头插法及其诡异,它不是从左到右,而是从右到左,这是一个值得注意的地方。