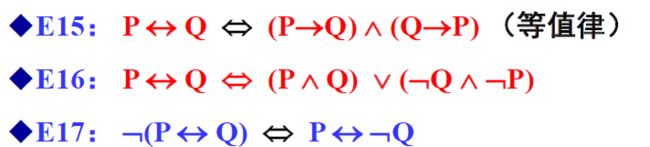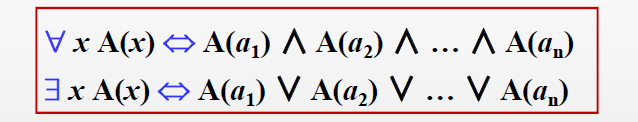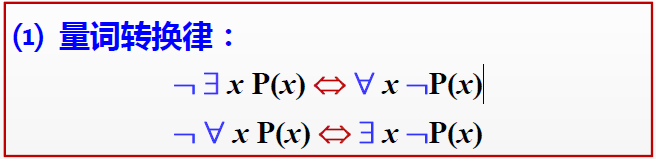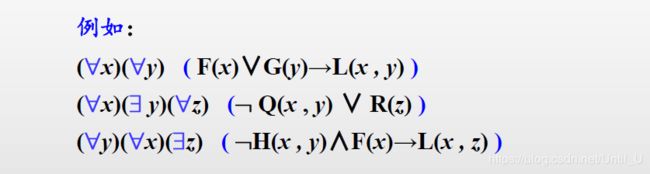离散数学笔记(期末复习用,持续更新…)
离散数学(又称计算机数学)是现代数学的重要分支,是计算机专业课程中的核心基础课程之一。
课程主要分四块:
• 第一部分 数理逻辑(第1章:命题逻辑、谓词逻辑)
• 第二部分 集合论(第2章:集合;第3章:二元关系;第4章:函数)
• 第三部分 代数系统 (第5章:无限集合;第6章:代数; 第7章:格和布尔代数)
• 第四部分 图 论 (第8章:图论)
目录
一、数理逻辑
1.1 命题逻辑
1.1.1 命题及其表示
1.1.2 命题公式
1.1.3 等价和蕴含
1.1.4 范式、主析取范式和主合取范式
1.1.5 推理理论
1.2 谓词逻辑
1.2.1 谓词和量词
1.2.2 谓词演算的永真式
一、数理逻辑
1.1 命题逻辑
1.1.1 命题及其表示
命题是陈述句,而不能是疑问句、命令句、感叹句等;命题真假用真值“真假”、“T,F”或“1,0”表示;
命题必须有真假,命题通常用大写英文字母表示,如 P、Q、R等。
命题联结词(否定,合取,析取,蕴含和等值)
否定,合取及析取容易理解;
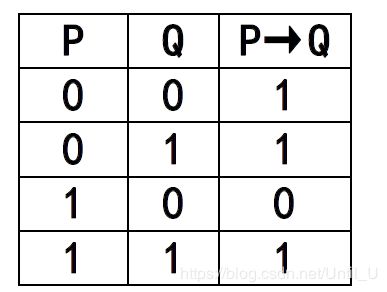
蕴含词:稍加注意的地方是:P→Q,P 称为蕴含前件、条件、前提;Q 称为后件、结果、结论。
当且仅当 P 为真,Q 为假时,P→Q 为假;否则, P→Q 均为真。真值表如下:
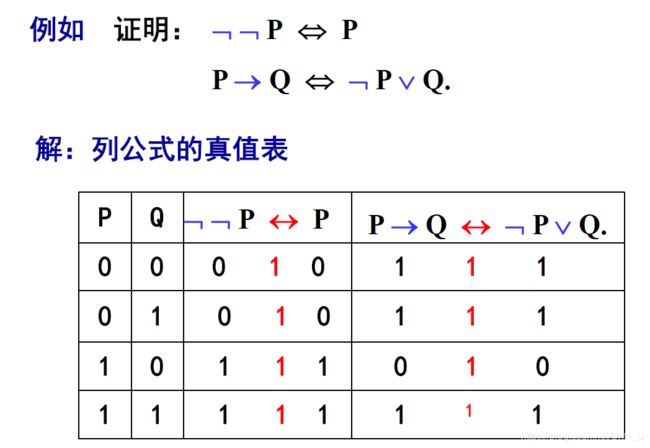
可以证明:
等值词:当且仅当P、Q的真值相同,即同为真或同为假时 P↔Q 为真;否则, P↔Q 为假。
1.1.2 命题公式
定义:由命题变元、常元、联结词、括号,以规定的格式联结起来的字符串。
注意:几元函数是由命题公式中命题变元个数决定的,例如P→ Q,两个变元就是2^2=4组真值指派;公式P→ (Q→ R) 可定义三元函数,这样真值表中就要列出2^3=8组真值指派。
《定义》:如果一个命题公式 A 的所有完全指派均为成真指派,则称公式 A 为重言式(永真式)。
《定义》:如果一个命题公式 A 的所有完全指派均为成假指派,则称公式 A 为矛盾式(永假式)。
《定义》:既不是永真式,又不是永假式,则称此命题公式是可满足式。
1.1.3 等价和蕴含
《定义》:如果对两个公式A,B不论作何种指派,它们的真值均相同,则称A,B是逻辑等价的,亦说A等价于B,记A⇔B.
例题:
定理:命题公式A⇔B的充要条件是A↔B为永真式。
等价式的性质:
1)自反性: A ⇔ A.
2)对称性: A ⇔ B,则 B ⇔ A.
3)传递性: A ⇔ B, B ⇔ C,则 A ⇔ C.
下面列出17组等价公式:
这十七个等价公式要记得,在后面的等价关系证明中要用到,用真值表有点麻烦(如果变元>=3,建议用公式替换化简),下面给几个例题练习下:
*还有对偶式的原理和求解,这个理解下就可以了:(注意式中如有→,⇔将其化成由联结词Λ,∨和﹁;并且括号不能去掉)
永真蕴含式
《定义》:命题公式A称为永真蕴含命题公式B,当且仅当A→B是一个永真式,记作:A=>B.
《定理》:给定命题公式A、B、C,若A=>B,且B=>C,则A=>C。
《定理》:给定命题公式A、B、C,若A=>B、A=>C,则 A => BΛC
例如 证明:P=> P∨Q; PΛQ => P。
下面给出13组常用的永真蕴含式:
1.1.4 范式、主析取范式和主合取范式
如何判定命题公式为永真式、永假式和可满足的呢?如何判定两个命题公式等价?(1)真值表法;(2)命题演算方法;(3)范式方法
范式:把命题公式化归为一种标准的形式,称此标准形式为范式。
(一)、范式:析取范式和合取范式:
设命题变元为:P、Q、R,
则:析取式(P∨Q∨R)称为“和”;合取式(P∧Q∧R)称为“积”。
析取范式和合取范式的定义如下:
求公式的析取范式和合取范式的步骤:
(1)利用等价公式,化去联结词“→”、“⇔” ,把命题公式变为与其等价的且用{﹁ ,∧,∨}表达的公式;
(2)将“﹁”深入到原子命题变元之前,并使变元之前最多只有一个“﹁”词;
(3)利用“∧”与“∨”的分配律,将公式化为析取范式(合取范式)。
(4)去掉永假项(永真项)得最简析取范式(最简合取范式)。
例题:
(二)、主析取范式和主合取范式
主析取范式:
《定义》给定一命题公式,其仅含有极小项析取的等价式称为给定命题公式的主析取范式。在真值表中,一个公式的真值为T的指派所对应的极小项的析取,即为此公式的主析取范式。
主合取范式:
《定理》在真值表中,一个公式的真值为F的指派所对应的极大项的合取,即为此公式的主合取范式。在真值表中真值为“F”的个数等于主合取范式中极大项的个数。
求解主合取范式和主析取范式时,可以通过真值表(前提变元<3的情况下,不然列出来很麻烦)
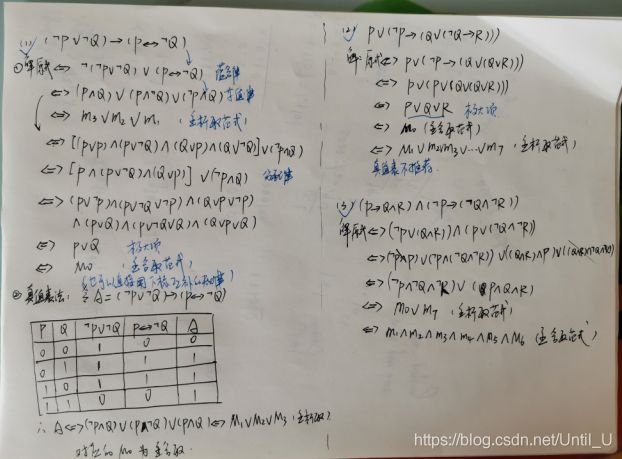
例题:求解下列各式的主析取范式和主合取范式(考试只考到3个变元的)
1.1.5 推理理论
直接证法:
•P 规则:在推导的任何步骤上,都可以引入前提。
•T 规则:在推导过程中,如果前面有一个或多个命题公式永真蕴含命题公式 S,那么就可以把公式 S 也引入到推导过程之中。
•置换规则:在推导的任何步骤上,命题公式中的子公式都可以用与之等价的公式置换。
间接证法:
1.2 谓词逻辑
1.2.1 谓词和量词
(1)个体
《定义》原子命题中表示主体或客体的词,称为个体。通常用a,b,c,…表示。个体它可以是独立存在的人或物体,也可以是
抽象的概念。
注: 个体域(论域):个体变元的取值范围。
- ①个体域可以是有穷集合,也可以是无穷集合。
- ②全总个体域:宇宙间的一切对象组成的集合。
- ③其它任意个体域都是全总个体域的子集。
- ④如无特别说明,所采用的都是全总个体域。
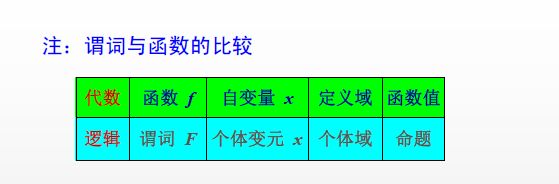
(2)谓词
《定义》用以刻画个体的属性或个体之间关系的模式,称为谓词。通常用大写字母 F,G,H,…表示。例如 张华是大学生。
- 一元谓词:与一个个体相关联的谓词。
- 二元谓词:与两个个体相关联的谓词。
- 一般的,把与 n 个个体相关联的谓词称为n元谓词。
(3)命题函数
《定义》一个谓词 F 后填上相关联的 n 个个体变元所得的表达式 F(x1 , x2 ,…, xn ),称为 n 元简单命题函数。
例如:
F(x) : x 是质数。 (一元命题函数)
H(x , y): x 大于 y。(二元命题函数)
显然,F(x),H(x , y)都不是命题,因为它们的真值无法判断。但若令 a:2, b:3 ,则
F(a) : 2 是质数,这是个真命题,它的真值为真。
H(a,b):2 大于3,这是个假命题,它的真值为假。
(4)量词
将命题符号化
个体域有两类:
-
特殊指定。(所有老虎组成的集合)则这时只 需对个体的属性进行谓词表示。
-
全总个体域。则还要运用特性谓词来限定研究的对象,即把研究对象从全总个体域中分离出来。没有指定个体域的话默认都用全总个体域
再看个二元命题的情况
(5)谓词公式
举一些例子就可以理解拉。将命题翻译成谓词公式
(6)变元的约束
1.2.2 谓词演算的永真式
谓词逻辑里也有谓词公式的等价与蕴含(跟命题逻辑一样)
(1)谓词演算的等价式
- 命题逻辑中等价式的推广
- 消去量词等价式
- 含有量词的等价式
(2)谓词演算的永真蕴含式
(3)含有多个量词的永真式
异名量词出现的次序直接关系到命题的含义:
(4) 前束范式
《定义》一个公式,如果量词均在全式的开头,它们的作用域延伸到整个公式的末尾,则称此公式叫前束范式。
《定理》任何一个谓词公式均与一个前束范式等价。且前束范式分为前束合取范式和前束析取范式。