python实现图的深度优先搜索(DFS)和广度优先搜索(BFS)算法及Dijkstra最短路径应用

  上篇文章介绍了树的常见遍历方式，这次我们一次来看看图的吧。深度优先搜索（Depth-First-Search）和广度优先搜索（Breadth-First-Search）是图论中比较重要的两种算法，面试题中经常遇到，我们主要看看python的实现代码，然后理论思想大家可以参考：深度优先遍历(DFS)和广度优先遍历(BFS)。
  我们以下图为例，分别介绍广度优先搜索和深度优先搜索。

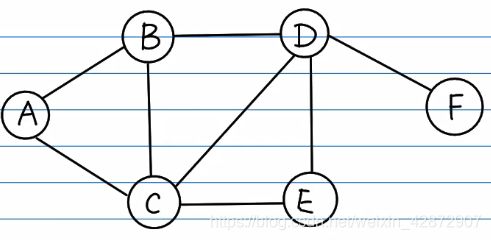
广度优先搜索：

#图节点
graph={
    'A':['B','C'],
    'B':['A','C','D'],
    'C':['A','B','D','E'],
    'D':['B','C','E','F'],
    'E':['C','D'],
    'F':['D']
}

// 广度优先搜索(BFS)
def BFS(graph,s):
    queue=[]   #建立队列
    queue.append(s)
    seen=[]    #记录已经遍历过的点
    seen.append(s)
    while queue:
        vertex=queue.pop(0)  #队列，先进先出
        nodes=graph[vertex]
        for w in nodes:
            if w not in seen:
                queue.append(w)
                seen.append(w)
        print(vertex)
       
BFS(graph,'A')

输出结果

深度优先搜索：

// 深度优先搜索(DFS)
def DFS(graph,s):
    stack=[]
    stack.append(s)
    seen=[]
    seen.append(s)
    while stack:
        vertex=stack.pop()  #栈，取出最后一个并删掉 先进后出
        nodes=graph[vertex]
        for w in nodes:
            if w not in seen:
                stack.append(w)
                seen.append(w)
        print(vertex)
        
DFS(graph,'A')

输出结果：

广度优先求出路径(多了一步-记录父节点)

// An highlighted block
#广度优先求最短路径
def min_BFS(graph,s):
    queue=[]
    queue.append(s)
    seen=[]
    seen.append(s)
    parent={s:None}

    while queue:
        vertex=queue.pop(0)  #队列，先进先出
        nodes=graph[vertex]
        for w in nodes:
            if w not in seen:
                queue.append(w)
                seen.append(w)
                parent[w]=vertex
        print(vertex)
    return parent



parent=min_BFS(graph,'E')
for i in parent:
    print(i,parent[i])

# 求得'E'->'B'最短距离
v='B'
while v:
    print(v)
    v=parent[v]

输出结果

路径：E->C->B

接下来是Dijkstra算法实现，节点和权重如下图。

// Dijkstra

import heapq
import math

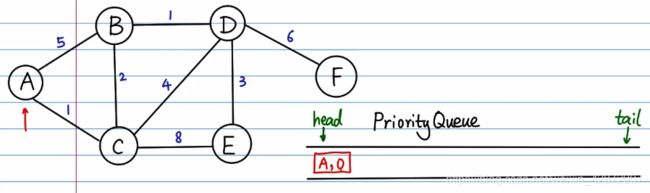
#定义图及路径
graph={
    'A':{'B':5,'C':1},
    'B':{'A':5,'C':2 ,'D':1},
    'C':{'A':1,'B':2,'D':4,'E':8},
    'D':{'B':1,'C':4,'E':3,'F':6},
    'E':{'C':8,'D':3},
    'F':{'D':6}
}

#初始化距离
def init_distance(graph,s):
    distance={s:0}
    for vertex in graph:
        if vertex != s:
            distance[vertex]=math.inf
    return distance

#dijkstra算法
def dijkstra(graph,s):
    queue=[]   #初始化队列
    heapq.heappush(queue,(0,s))  #放入第一个元素
    seen=[]     #已经取出来的
    parent={s:None}    #父节点
    distance=init_distance(graph,s)   #初始化距离

    while queue:
        pair=heapq.heappop(queue)  #heapq每次加入后自动排序，heappop每次取把距离小的放前面，取出来的格式为(0,s)
        cur_dist=pair[0]   #当前的距离
        vertex=pair[1]     #当前的节点
        nodes=graph[vertex].keys()   #该节点下的相邻各个节点
        seen.append(vertex)

        for n in nodes:
            if n not in seen:
                if cur_dist+graph[vertex][n]<distance[n]:
                    heapq.heappush(queue,(cur_dist+graph[vertex][n],n))
                    distance[n]=cur_dist+graph[vertex][n]
                    parent[n]=vertex

    return parent,distance


parent,distance=dijkstra(graph,'A')
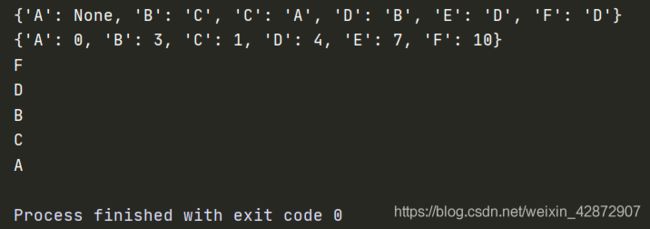
print(parent)
print(distance)

#根据节点倒推，输出A->F最短路径
v='F'
while v:
    print(v)
    v=parent[v]

输出结果：

得到最短路径为：A->C->B->D->F。

参考视频：https://www.bilibili.com/video/BV1LZ4y1j7JY?p=3